AUSTRALIAN MATHS TRUST 2019
TIME ALLOWED: 75 minutes
INSTRUCTIONS AND INFORMATION
General
1 Do not open the booklet until told to do so by your teacher.
2 NO calculators, maths stencils, mobile phones or other calculating aids are permitted. Scribbling paper, graph paper, ruler and compasses are permitted, but are not essential.
3 Diagrams are NOT drawn to scale. They are intended only as aids.
4 There are 25 multiple-choice questions, each requiring a single answer, and 5 questions that require a whole number answer between 0 and 999 . The questions generally get harder as you work through the paper. There is no penalty for an incorrect response.
5 This is a competition not a test; do not expect to answer all questions. You are only competing against your own year in your own country/Australian state so different years doing the same paper are not compared.
6 Read the instructions on the answer sheet carefully. Ensure your name, school name and school year are entered. It is your responsibility to correctly code your answer sheet.
7 When your teacher gives the signal, begin working on the problems
The answer sheet
1 Use only lead pencil.
2 Record your answers on the reverse of the answer sheet (not on the question paper) by FULLY colouring the circle matching your answer.
3 Your answer sheet will be scanned. The optical scanner will attempt to read all markings even if they are in the wrong places, so please be careful not to doodle or write anything extra on the answer sheet. If you want to change an answer or remove any marks, use a plastic eraser and be sure to remove all marks and smudges.
Integrity of the competition
The AMT reserves the right to re-examine students before deciding whether to grant official status to their score.
Reminder: You may sit this competition once, in one division only, or risk no score.
1-10 题, 每题 3 分
Questions 1 to10,3marks each
The value of \( {20.19} - {19} \) is
(A) 39.19 (B) 20.38 (C) 20 (D) 1.19 (E) 1
__________

(A) 下午 3: 30 (B) 下午 3: 40 (C) 下午 3: 50 (D) 下午 4: 40 (E) 下午 4: 50 Sharyn’s piano lesson was 40 minutes long, and finished at \( 4 : {10}\mathrm{{pm}} \) . When did it start?
(A) \( 3 : {30}\mathrm{{pm}} \) (B) \( 3 : {40}\mathrm{{pm}} \) (C) \( 3 : {50}\mathrm{{pm}} \) (D) \( 4 : {40}\mathrm{{pm}} \) (E) \( 4 : {50}\mathrm{{pm}} \)
__________
Which of the following is closest to \( 7 \times {1.8} \) ?
(A) 10 (B) 11 (C) 12 (D) 13 (E) 14
__________
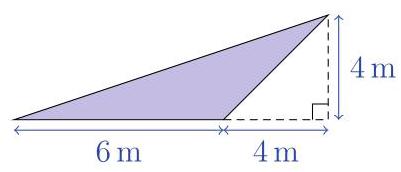
What is the area of the shaded triangle?
(A) \( 8{\mathrm{\;m}}^{2} \) (B) \( {12}{\mathrm{\;m}}^{2} \) (C) \( {14}{\mathrm{\;m}}^{2} \)
(D) \( {20}{\mathrm{\;m}}^{2} \) (E) \( {24}{\mathrm{\;m}}^{2} \)
Five-eighths of a number is 200 . What is the number?
(A) 120 (B) 320 (C) 275 (D) 75 (E) 280
| 1 | ||
| 2 | \( N \) | |
| \( M \) |
请问 \( N + M \) 之值是什么?
Every row and every column of this \( 3 \times 3 \) square must contain each of the numbers 1,2 and 3 .
What is the value of \( N + M \) ?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
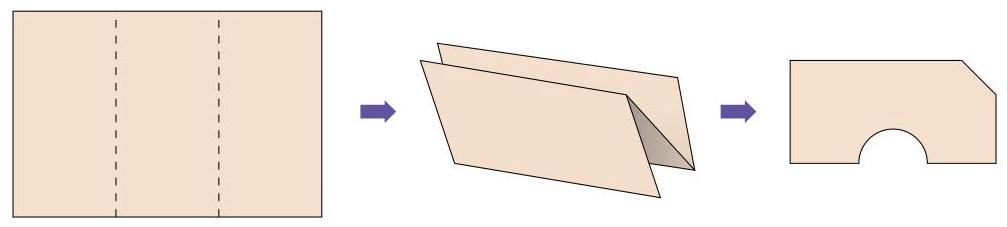
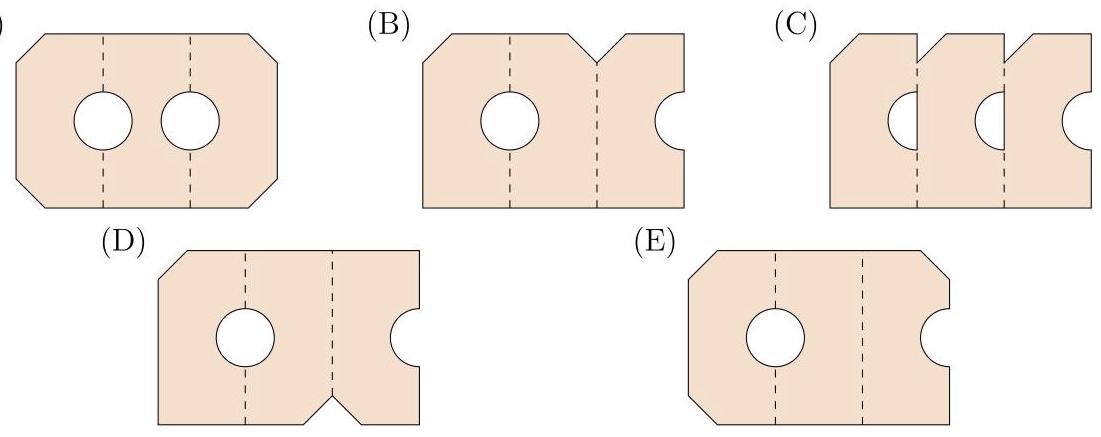
当将这张纸展开, 请问它看起来是哪一个选项?
When the paper is unfolded, what does it look like?
(A)
When a rectangle is cut in half, two squares are formed. If each square has a perimeter of 48 , what is the perimeter of the original rectangle?
(A) 96 (B) 72 (C) 36 (D) 24 (E) 12
\[ 1,4,7,4,1,4,7,4,1,4,\ldots , \]
它每四项循环。最前 3 项的累计总和是 12 ,最前 7 项的累计总和是 28 。
请问下列哪一个选项内的值可能是这个数列的累计总和?
Consider the undulating number sequence
\[ 1,4,7,4,1,4,7,4,1,4,\ldots , \]
which repeats every four terms. The running total of the first 3 terms is 12 . The running total of the first 7 terms is 28 .
Which one of the following is also a running total of this sequence?
(A) 61 (B) 62 (C) 67 (D) 66 (E) 65
Sebastien has a Personal Identification Number (PIN) consisting of four digits. The first three digits in order are 591. If Sebastien's PIN is divisible by 3 , then how many possibilities are there for the final digit?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
11-20 题,每题 4 分
Questions 11 to 20, 4 marks each
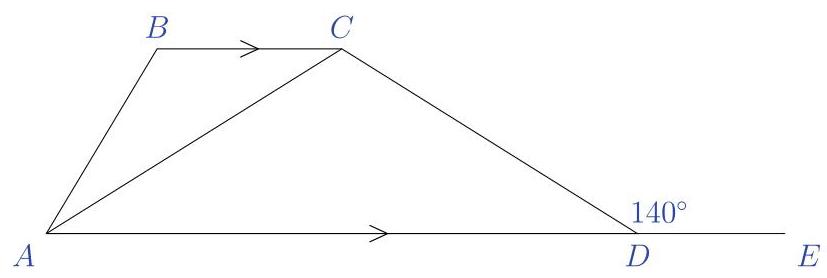
(A) 90 (B) 100 (C) 110 (D) 120 (E) 130
In my dance class, 14 students are taller than Bob, and 12 are shorter than Alice. Four students are both shorter than Alice and taller than Bob. How many students are in my dance class?
(A) 22 (B) 24 (C) 26 (D) 28 (E) 30
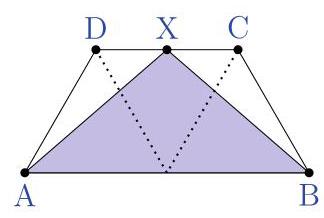
点 \( X \) 是 \( {CD} \) 的中点。
请问涂上阴影部份的面积占四边形 \( {ABCD} \) 面积的几分之几?
Three equilateral triangles are joined to form the quadrilateral \( {ABCD} \) shown.
The point \( X \) is halfway along \( {CD} \) .
What fraction of the area of \( {ABCD} \) is shaded?
(A) \( \frac{1}{2} \) (B) \( \frac{3}{4} \) (C) \( \frac{2}{3} \) (D) \( \frac{5}{6} \) (E) \( \frac{3}{5} \)
右撇子与左撇子学生人数之比为 4:1 , 而 15 岁学生人数与 16 岁学生人数之比为 1: 2, 且 15 岁左撇子人数与 16 岁左撇子人数之比为 1: 5。
将这一班所有学生的名牌放进一顶帽子内, 从中随机抽出一个, 请问抽出的学生是 15 岁且是右撇子的机率是什么?
In a year 10 Maths class, there are 30 students. Each student is either 15 or 16 years old, and either left- or right-handed.
The ratio of right-handed students to left-handed students is \( 4 : 1 \) , the ratio of 15 year olds to 16 year olds is \( 1 : 2 \) and the ratio of left-handed 15 year olds to left-handed 16 year olds is 1 : 5 .
If the names of the students in this class are placed in a hat and one is selected at random, what is the probability that the student selected is 15 years old and right-handed?
(A) \( \frac{1}{30} \) (B) \( \frac{1}{6} \) (C) \( \frac{3}{10} \) (D) \( \frac{1}{2} \) (E) \( \frac{4}{5} \)
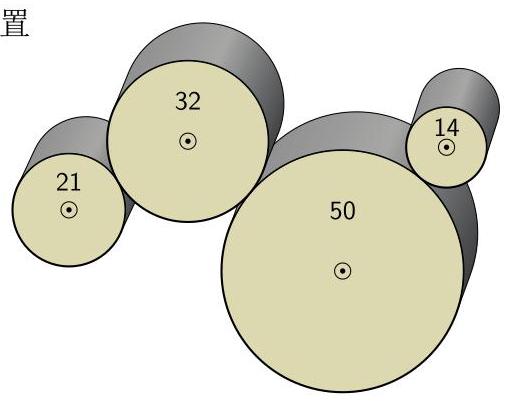
\( {32}\mathrm{\;{cm}} \) 、 \( {50}\mathrm{\;{cm}} \) 、 \( {14}\mathrm{\;{cm}} \) 。
当 \( {21}\mathrm{\;{cm}} \) 的这个滚轴转一整圈 \( \left( {360}^{ \circ }\right) \) ,
请问 \( {14}\mathrm{\;{cm}} \) 的这个滚轴转动的角度为多少?
The set of four rollers shown has fixed axles and transfers rotation from each roller to the next without slipping. Their diameters are \( {21}\mathrm{\;{cm}},{32}\mathrm{\;{cm}},{50}\mathrm{\;{cm}} \) and \( {14}\mathrm{\;{cm}} \) respectively.
While the \( {21}\mathrm{\;{cm}} \) roller makes a full rotation \( \left( {360}^{ \circ }\right) \) , through which angle does the \( {14}\mathrm{\;{cm}} \) roller rotate?
(A) 180° (B) \( {310}^{ \circ } \) (C) 360° (D) \( {540}^{ \circ } \) (E) \( {620}^{ \circ } \)
请问现在的箱子中总共有多少颗苹果?
In a box of apples, \( \frac{3}{7} \) of the apples are red and the rest are green. Five more green apples are added to the box. Now \( \frac{5}{8} \) of the apples are green.
How many apples are there now in the box?
(A) 32 (B) 33 (C) 38 (D) 40 (E) 48
如果最后这三个被宣布出的数之和是 7 的倍数, 则小亚获胜, 否则小莉获胜。
请问小亚第一次应该选哪一个数才能保证获胜?
Asha chooses a whole number from 1 to 5 and announces it. Then Richy chooses a whole number from 1 to 5 and announces it. Finally, Asha chooses a whole number from 1 to 5 and announces it.
If the sum of the three numbers announced is a multiple of 7 , then Asha wins; otherwise, Richy wins.
What number should Asha choose on her first turn to guarantee that she can win?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
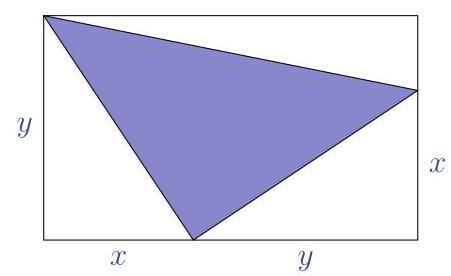
The area of the shaded triangle inside this rectangle is
(A) \( \frac{1}{2}{\left( x + y\right) }^{2} \) (B) \( x\left( {x + y}\right) \) (C) \( y\left( {x + y}\right) \)
(D) \( \frac{1}{2}\left( {{y}^{2} - {x}^{2}}\right) \) (E) \( \frac{1}{2}\left( {{x}^{2} + {y}^{2}}\right) \)

现在将这些正立方体排成一列, 使得从正前方看过去它们的样子如下:

当我们从这些正立方体的正后方看过去时, 请问我们将看到什么? (A)
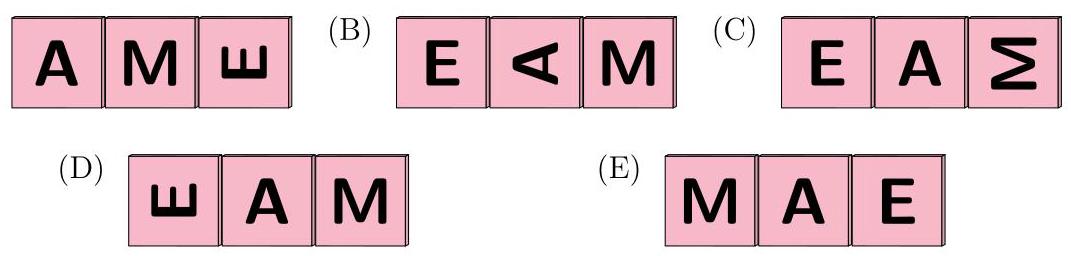
These three cubes are labelled in exactly the same way, with the 6 letters A, M, C, \( \mathrm{D},\mathrm{E} \) and \( \mathrm{F} \) on their 6 faces:
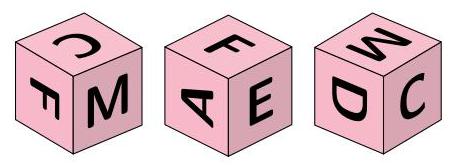
The cubes are now placed in a row so that the front looks like this:
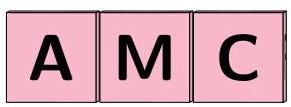
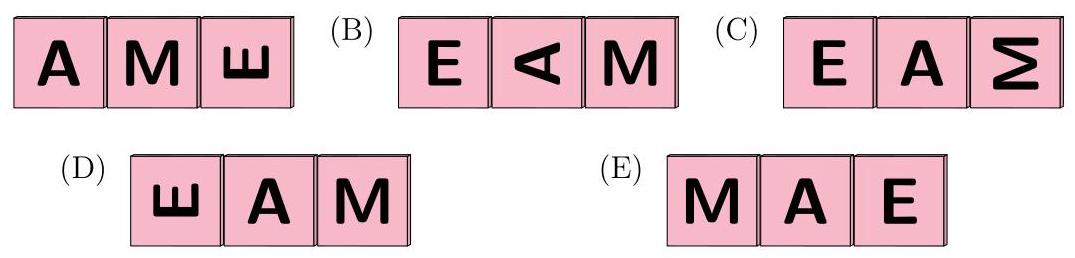
When we look at the cubes from the opposite side, we will see
(A)
Five numbers are placed in a row. From the third number on, each number is the average of the previous two numbers. The first number is 12 and the last number is 7 . What is the third number?
(A) 4 (B) 5 (C) 6 (D) 7 (E) 8
21-25 题,每题 5 分 Questions 21 to 25,5 marks each
如果只使用第一根水管,则费时 21 小时可将水池注满水。如果只使用第二根水管, 则费时 24 小时可将水池注满水。如果三根水管一起使用, 则费时 8 小时可将水池注满水。
如果只使用第三根水管, 请问需费时多久才可以将水池注满?
(A) 12 小时 (B) 14 小时 (C) 27 小时 (D) 28 小时 (E) 30 小时
How long will it take to fill the pool using only the third pipe?
(A) 12 hours (B) 14 hours (C) 27 hours (D) 28 hours (E) 30 hours
现在将这个平台净空, 然后放上若干个正立方体, 它的前视图与右视图如下图所示。
请问在这个平台上最多可以有多少个正立方体?
前侧 FRONT 右侧 RIGHT
The board is cleared, then a number of these cubes are placed on the grid. The front and right side views are shown.
What is the maximum number of cubes there could be on the board?
(A) 10 (B) 11 (C) 16 (D) 17 (E) 18
(i) 如果他靠近他家,则他走路回家,然后改成驾车上班。
(ii) 如果他靠近工作地点,则剩下的路程他改用步行的方式。
(iii) 如果在中点附近,则花费 20 分钟修理自行车的轮胎然后继续骑车上班。
他知道在前往工作地点的途中, 有二个位置必须改变策略。请问这两个位置的距离是什么?
Manny has three ways to travel the 8 kilometres from home to work: driving his car takes 12 minutes, riding his bike takes 24 minutes and walking takes 1 hour and 44 minutes. He wants to know how to get to work as quickly as possible in the event that he is riding his bike and gets a flat tyre.
He has three strategies:
(i) If he is close to home, walk back home and then drive his car.
(ii) If he is close to work, just walk the rest of the way.
(iii) For some intermediate distances, spend 20 minutes fixing the tyre and then continue riding his bike.
He knows there are two locations along the route to work where the strategy should change. How far apart are they?
(A) \( 2\mathrm{\;{km}} \) (B) \( 3\mathrm{\;{km}} \) (C) \( 4\mathrm{\;{km}} \) (D) \( 5\mathrm{\;{km}} \) (E) \( 6\mathrm{\;{km}} \)
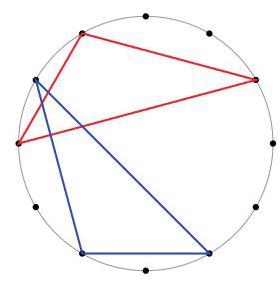
在一个圆周上有十二个等距离的点。连接其中三个点可以构造一个三角形。
如果两个三角形经过旋转, 但不可以翻转, 会完全吻合在一起, 则视这两个三角形为相同的。例如, 右图所示的两个三角形是相同的。
请问总共可以构造出多少个不同的三角形?
Out of modern musical theory comes the following question.
Twelve points are equally spaced around a circle. Three points are to be joined to make a triangle.
We count two triangles as being the same only if they match perfectly after rotating, but not reflecting. For instance, the two triangles shown are the same.
How many different triangles can be made?
(A) 10 (B) 14 (C) 19 (D) 20 (E) 22

当这枚硬币回到出发点时,它恰好转一整圈。
请问这正方形的边长为多少 \( \mathrm{{cm}} \) ?
When it returns to where it started, the coin has performed exactly one whole revolution.
In centimetres, what is the side length of the square?
(A) \( \pi \) (B) 3.5 (C) \( 1 + \pi \) (D) 4 (E) \( 2 + \frac{\pi }{2} \)
问题 26-30 的答案为 000-999 之间的整数,
请将答案填在答案卡上对应的位置。
第 26 题占 6 分,第 27 题占 7 分,第 28 题占 8 分, 第 29 题占 9 分,第 30 题占 10 分。
For questions 26 to 30, shade the answer as an integer from 0 to 999
in the space provided on the answer sheet.
Questions 26-30 are worth 6, 7, 8, 9 and 10 marks, respectively.
When I divide an integer by 15 , the remainder is an integer from 0 to 14 . When I divide an integer by 27 , the remainder is an integer from 0 to 26 .
For instance, if the integer is 100 then the remainders are 10 and 19, which are different.
How many integers from 1 to 1000 leave the same remainders after division by 15 and after division by 27?
找出所有二位数中, 当我们把它的数码全部加上 2 , 然后相乘, 最后所得的结果与原数值相同。请问满足上述条件的所有二位数之和是什么?
The number 35 has the property that when its digits are both increased by 2 , and then multiplied, the result is \( 5 \times 7 = {35} \) , equal to the original number.
Find the sum of all two-digit numbers such that when you increase both digits by 2 , and then multiply these numbers, the product is equal to the original number.
因此在这个国家的初始几个计数数为 1、2、3、4、5、6、7、8、9、11、12、...,其中第十个数是 11。
当您写下初始一千个该国允许的计数数时, 请问最后一个数的末三位数码是什么?
The Leader of Zip decrees that the digit 0 , since it represents nothing, will no longer be used in any counting number. Only counting numbers without 0 digits are allowed. So the counting numbers in Zip begin 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, ..., where the tenth counting number is 11 .
When you write out the first one thousand allowable counting numbers in Zip, what are the last three digits of the final number?
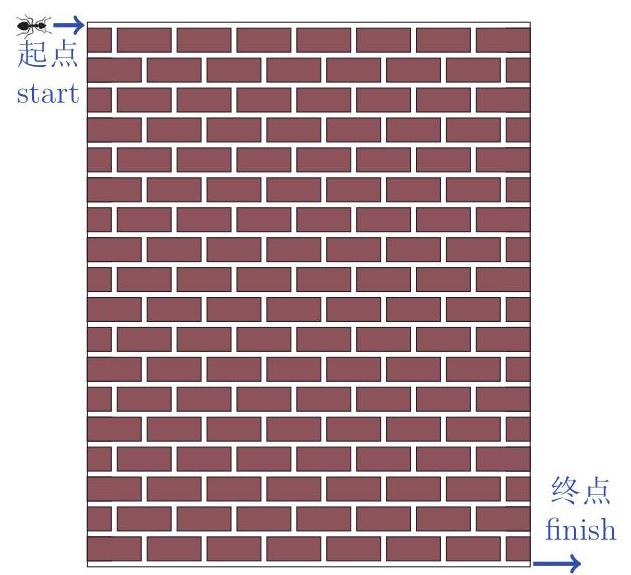
由于天气炎热,牠避免爬上深色的砖面只敢在砖块之间与砖墙最上层、最下层较冷的白色水泥中爬行。
这道砖墙排有 18 行砖, 每行有七整块又半块的砖, 它们以交错的形式排列,如图所示。 请问这只蚂蚁要爬行到对角的最快路径总共有多少种不同的方法?
Antony the ant is at the top-left corner of this brick wall and needs to get to the bottom-right corner.
Because it is a hot day, he avoids the dark bricks and only walks on the cooler white mortar between the bricks and at the top and bottom of the wall.
There are 18 rows of bricks, each with 7 whole bricks and one half-brick in an alternating pattern.
How many different ways are there for Antony to walk to the opposite corner as quickly as possible?
草稿纸
Scratch Paper
草稿纸
Scratch Paper