CHINESE VERSION

NAME

TIME ALLOWED: 75 MINUTES

INSTRUCTIONS AND INFORMATION

General

Do not open the booklet until told to do so by your teacher.

NO calculators, maths stencils, mobile phones or other calculating aids are permitted. Scribbling paper, graph paper, ruler and compasses are permitted, but are not essential.

Diagrams are NOT drawn to scale. They are intended only as aids.

There are 25 multiple-choice questions, each requiring a single answer, and 5 questions that require a whole number answer between 0 and 999 . The questions generally get harder as you work through the paper. There is no penalty for an incorrect response.

This is a competition not a test; do not expect to answer all questions. You are only competing against your own year in your own country/Australian state so different years doing the same paper are not compared.

Read the instructions on the answer sheet carefully. Ensure your name, school name and school year are entered. It is your responsibility to correctly code your answer sheet.

When your teacher gives the signal, begin working on the problems.

The answer sheet

Use only lead pencil.

Record your answers on the reverse of the answer sheet (not on the question paper) by FULLY colouring the circle matching your answer.

Your answer sheet will be scanned. The optical scanner will attempt to read all markings even if they are in the wrong places, so please be careful not to doodle or write anything extra on the answer sheet. If you want to change an answer or remove any marks, use a plastic eraser and be sure to remove all marks and smudges.

Integrity of the competition

The AMT reserves the right to re-examine students before deciding whether to grant official status to their score.

Reminder: You may sit this competition once, in one division only, or risk no score.

1-10 题, 每题 3 分

Questions 1 to10,3marks each

计算 \( 2 - \left( {0 - \left( {2 - 0}\right) }\right) = \)

\( 2 - \left( {0 - \left( {2 - 0}\right) }\right) = \)

(A) -4 (B) -2 (C) 0 (D) 2 (E) 4

请问 2 的 1000% 等于多少?

1000% of 2 is equal to

(A) 0.002 (B) 20 (C) 200 (D) 1002 (E) 2000

在右图中,请问 \( x \) 与 \( y \) 之和等于多少?

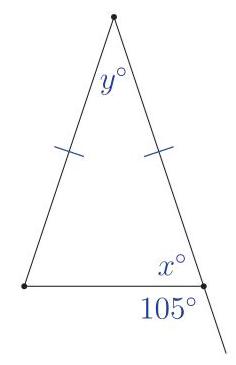
In the diagram provided, find the sum of \( x \) and \( y \) .

(A) 30 (B) 75 (C) 95

(D) 105 (E) 180

计算 \( \frac{1 + 2 + 3 + 4 + 5}{1 + 2 + 3 + 4} - \frac{1 + 2}{1 + 2 + 3} = \)

\( \frac{1 + 2 + 3 + 4 + 5}{1 + 2 + 3 + 4} - \frac{1 + 2}{1 + 2 + 3} = \)

(A) 3 (B) \( \frac{5}{6} \) (C) 1 (D) \( \frac{7}{6} \) (E) 2

小莎心里想着两个数,它们的和为 26 、差为 14 。请问小莎想的这两个数的乘积是多少?

Sebastien is thinking of two numbers whose sum is 26 and whose difference is 14 . The product of Sebastien's two numbers is

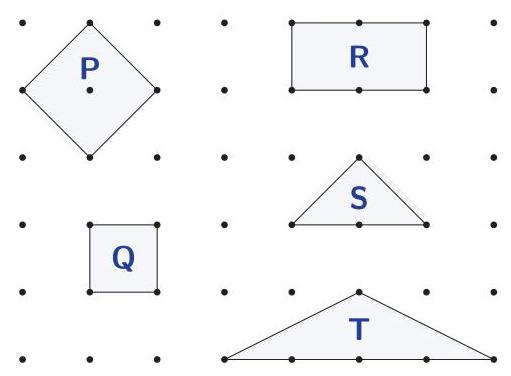
(A) 80 (B) 96 (C) 105 (D) 120 (E) 132 6. 右图中哪些图形的面积相等? (A) 所有图形的面积都相等。 (B) 只有 \( \mathrm{Q} \) 与 \( \mathrm{S} \) 的面积相等。 (C) 只有 \( \mathrm{R} \) 与 \( \mathrm{T} \) 的面积相等。 (D) 只有 \( \mathrm{P} \) 、 \( \mathrm{R} \) 与 \( \mathrm{T} \) 的面积相等。 (E) \( \mathrm{P}\text{、}\mathrm{R} \) 与 \( \mathrm{T} \) 的面积相等且 \( \mathrm{Q} \) 与 \( \mathrm{S} \) 的面积相等。 Which of the shapes in the diagram have equal area? (A) All of the shapes have equal area. (B) Only \( \mathrm{Q} \) and \( \mathrm{S} \) have equal area. (C) Only \( \mathrm{R} \) and \( \mathrm{T} \) have equal area. (D) Only P, R and T have equal area. (E) \( \mathrm{P},\mathrm{R} \) and \( \mathrm{T} \) have equal area, and \( \mathrm{Q} \) and \( \mathrm{S} \) have equal area.

\( {123456} - {12345} + {1234} - {123} + {12} - 1 = \) (A) 33333 (B) 101010 (C) 111111 (D) 122223 (E) 112233 8. 已知 \( \frac{7}{8} \) 的 \( \frac{x}{7} \) 的 \( \frac{5}{6} \) 的 \( \frac{4}{5} \) 等于 1,请问 \( \star \) 的值为多少? If \( \frac{4}{5} \) of \( \frac{5}{6} \) of \( \frac{ \star }{7} \) of \( \frac{7}{8} \) is equal to 1, then the value of \( \star \) is (A) 6 (B) 8 (C) 10 (D) 12 (E) 14

将一张纸片依下图所示折叠两次,然后沿着虚线剪掉两侧部分后,将它展开。

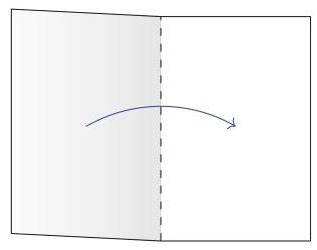
请问最像哪个英文字母?

A piece of paper is folded twice as shown and cut along the dotted lines.

Once unfolded, which letter does the piece of paper most resemble?

(A) M (B) O (C) \( \mathrm{N} \) (D) B (E) V

10.

将一个正三角形分割成若干个小正三角形, 如图所示。涂上阴影的三角形边长为 2。

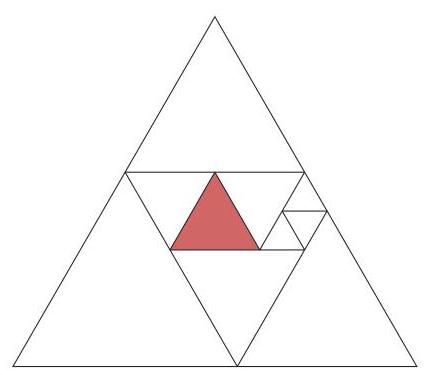
请问原来这个大正三角形的周长是多少?

An equilateral triangle is subdivided into a number of smaller equilateral triangles, as shown. The shaded triangle has side length 2 . What is the perimeter of the large triangle?

(A) 24 (B) 27 (C) 30

(D) 33 (E) 36

11-20 题,每题 4 分

Questions 11 to 20, 4 marks each

11.

三角形 \( {XYS} \) 被矩形 \( {PQRS} \) 封闭在内, 如右图所示。

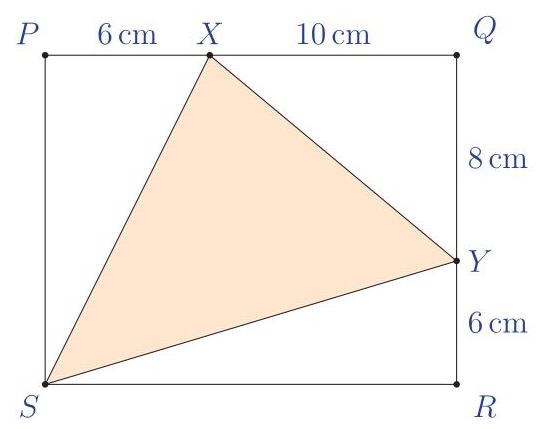
请问三角形 \( {XYS} \) 的面积为多少 \( {\mathrm{{cm}}}^{2} \) ？

Triangle \( {XYS} \) is enclosed by rectangle \( {PQRS} \) as shown in the diagram.

In square centimetres, what is the area of triangle \( {XYS} \) ?

(A) 82 (B) 88 (C) 94

(D) 112 (E) 130

12.

令 \( X = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11}\text{、}Y = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} \) 。请问 \( X - Y \) 等于什么?

Let \( X = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} \) and \( Y = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} \) . Then \( X - Y \) is equal to

(A) \( \frac{2}{99} \) (B) \( \frac{1}{11} \) (C) \( \frac{1}{10} \) (D) \( \frac{1}{2} \) (E) \( \frac{2}{9} \)

13.

25 可以写成三个小于 20 且互不相同的质数之和。例如 \( {25} = 5 + 7 + {13} \) 。请问有多少个 10 的整倍数可以写成三个小于 20 且互不相同的质数之和?

The number 25 can be written as the sum of three different primes less than 20 . For instance, \( {25} = 5 + 7 + {13} \) .

How many multiples of 10 can be written as the sum of three different primes less than 20?

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

14.

在圆心为 \( O \) 的圆内画出四个三角形,它们的角度如图所示。请问 \( x \) 的值等于多少?

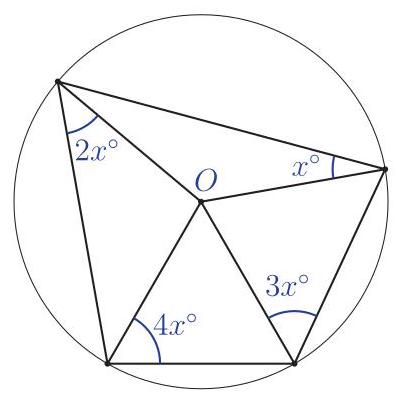
In this circle with centre \( O \) , four triangles are drawn, with angles as shown. What is the value of \( x \) ?

(A) 10 (B) 15 (C) 18

(D) 24 (E) 36

15.

已知教室里共有 10 名学生。如果另一名男生与另一名女生进入教室, 则男生对女生的比例会增加。请问一开始这间教室里最多可以有多少名男生?

There are 10 children in a classroom. The ratio of boys to girls increases when another girl and another boy enter the room. What is the greatest number of boys that could have been in the room at the beginning?

(A) 1 (B) 4 (C) 5 (D) 6 (E) 9

16.

两个三角形 \( A \) 与 \( B \) 的面积相等。三角形 \( A \) 是等腰三角形、三角形 \( B \) 是直角三角形。

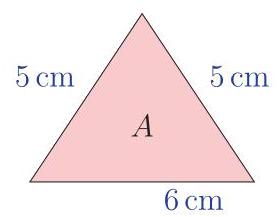
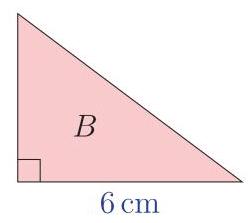
请问三角形 \( A \) 的周长与三角形 \( B \) 的周长之差为多少?

(A) \( 0\mathrm{\;{cm}} \) (B) 介于 \( 0\mathrm{\;{cm}} \) 与 \( 1\mathrm{\;{cm}} \) 之间 (C) 介于 \( 1\mathrm{\;{cm}} \) 与 \( 2\mathrm{\;{cm}} \) 之间

(D) 介于 \( 2\mathrm{\;{cm}} \) 与 \( 3\mathrm{\;{cm}} \) 之间 (E) 超过 \( 3\mathrm{\;{cm}} \)

Two triangles, \( A \) and \( B \) , have the same area. Triangle \( A \) is isosceles and triangle \( B \) is right-angled.

The difference between the perimeters of triangle \( A \) and triangle \( B \) is

(A) nothing (B) between \( 0\mathrm{\;{cm}} \) and \( 1\mathrm{\;{cm}} \) (C) between \( 1\mathrm{\;{cm}} \) and \( 2\mathrm{\;{cm}} \)

(D) between \( 2\mathrm{\;{cm}} \) and \( 3\mathrm{\;{cm}} \) (E) more than \( 3\mathrm{\;{cm}} \)

17.

有一列数的首项为 2 且第二项为 5 , 第三项与之后的每一项都等于前两项的乘积:

\[ 2,5,{10},{50},{500},\ldots \]

请问第八项是多少？

A list of numbers has first term 2 and second term 5 . The third term, and each term after this, is found by multiplying the two preceding terms together:

\( 2,5,{10},{50},{500},\ldots \)

The value of the eighth term is

(A) \( {2}^{5} \times {5}^{8} \) (B) \( {2}^{8} \times {5}^{9} \) (C) \( {2}^{8} \times {5}^{13} \) (D) \( {2}^{9} \times {5}^{15} \) (E) \( {2}^{13} \times {5}^{21} \)

18.

将一个正六边形的两边延长而构成一个小三角形。然后在这个小三角形内画出一个小正六边形, 如图所示。请问大正六边形的面积是小正六边形面积的几倍?

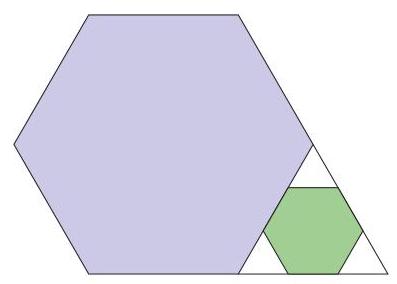
Two sides of a regular hexagon are extended to create a small triangle.

Inside this triangle, a smaller regular hexagon is drawn, as shown.

In area, how many times bigger is the larger hexagon than the smaller hexagon?

(A) 4 (B) 6 (C) 8 (D) 9 (E) 12

19.

算式 \( \frac{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9 \times {10}}{n} \) 的值是一个完全平方数。

请问 n 的最小可能值是多少?

The number \( \frac{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9 \times {10}}{n} \) is a perfect square.

What is the smallest possible value of \( n \) ?

(A) 7 (B) 14 (C) 21 (D) 35 (E) 70

20.

如右图,在三角形 \( {ABC} \) 中,点 \( D \) 是 \( {AC} \) 的中点、点 \( E \) 是 \( {BD} \) 的中点且点 \( F \) 是 \( {AE} \) 的中点。

(D) 45 (E) 50

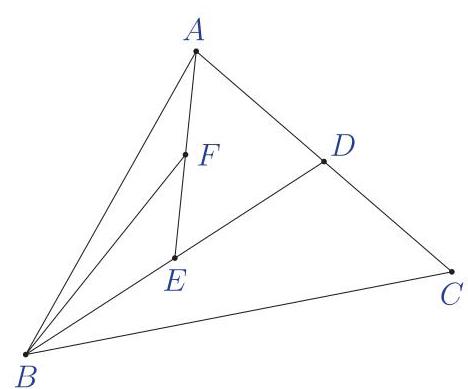
已知三角形 \( {BEF} \) 的面积为 5 平方单位,请问三角形 \( {ABC} \) 的面积为多少平方单位?

In the triangle \( {ABC} \) shown, \( D \) is the midpoint of \( {AC}, E \) is the midpoint of \( {BD} \) and \( F \) is the midpoint of \( {AE} \) .

If the area of triangle \( {BEF} \) is 5 , what is the area of triangle \( {ABC} \) ?

(A) 30 (B) 35 (C) 40

21-25 题,每题 5 分

Questions 21 to 25,5 marks each

21.

一名科学家研究几个星期内培养皿中的细菌数量, 并同时记录在这期间的温度和湿度。

检测结果表示在下面表格中。

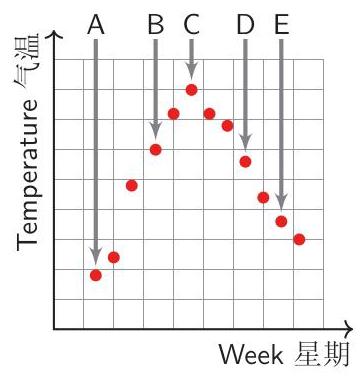
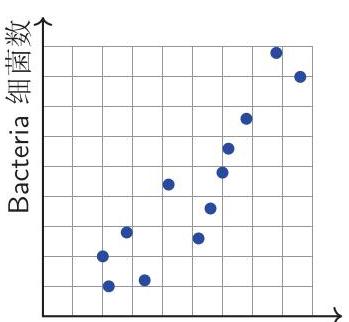
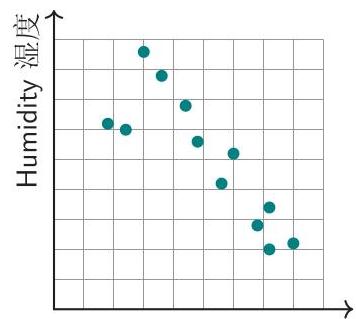
Humidity 湿度 Temperature 温度

请问哪个星期的细菌数量达到最高峰?

(A) A 星期 (B) B 星期 (C) C 星期 (D) D 星期 (E) E 星期

A scientist measured the amount of bacteria in a Petri dish over several weeks and also recorded the temperature and humidity for the same time period. The results are summarised in the graphs.

During which week was the bacteria population highest?

(A) week A (B) week B (C) week C (D) week D (E) week E

22.

A、B、C、D、E 五个人在假期共阅读了 40 本书。每个人至少阅读一本书,

但每个人阅读的书都各不相同。

已知 \( \mathrm{A} \) 阅读的数量是 \( \mathrm{E} \) 的两倍、 \( \mathrm{D} \) 阅读的数量是 \( \mathrm{B} \) 的两倍、 \( \mathrm{C} \) 阅读的数量

等于 \( \mathrm{D} \) 与 \( \mathrm{E} \) 阅读数量的总和。

请问哪个人恰好阅读了八本书?

(A) A (B) B (C) \( \mathrm{C} \) (D) D (E) \( \mathrm{E} \)

Five friends read a total of 40 books between them over the holidays. Everyone read at least one book but no-one read the same book as anyone else.

Asilata read twice as many books as Eammon. Dane read twice as many as Bettina. Collette read as many as Dane and Eammon put together.

Who read exactly eight books?

(A) Asilata (B) Bettina (C) Colette (D) Dane (E) Eammon

23.

有 5 根木棒长度分别为 \( 2\mathrm{\;{cm}} \) 、 \( 3\mathrm{\;{cm}} \) 、 \( 4\mathrm{\;{cm}} \) 、 \( 5\mathrm{\;{cm}} \) 与 \( 8\mathrm{\;{cm}} \) 。从中随机取出三根木棒。请问选出的木棒可以构成一个三角形的概率是多少?

There are 5 sticks of length \( 2\mathrm{\;{cm}},3\mathrm{\;{cm}},4\mathrm{\;{cm}},5\mathrm{\;{cm}} \) and \( 8\mathrm{\;{cm}} \) . Three sticks are chosen randomly. What is the probability that a triangle can be formed with the chosen sticks?

(A) 0.25 (B) 0.3 (C) 0.4 (D) 0.5 (E) 0.6

24.

将五个单位面积的正方形按照右图所示的方式

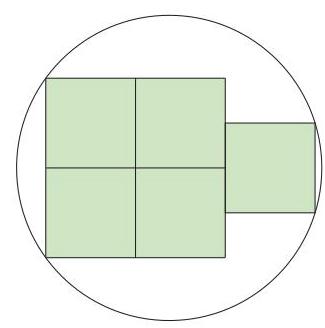
内接于一个圆内。请问这个圆的半径是多少单位？

Five squares of unit area are circumscribed by a circle as shown.

What is the radius of the circle?

(A) \( \frac{3}{2} \) (B) \( \frac{2\sqrt{5}}{3} \) (C) \( \frac{\sqrt{10}}{2} \) (D) \( \frac{\sqrt{13}}{2} \) (E) \( \frac{\sqrt{185}}{8} \)

25.

小亚计算以下算式的和,算式中最后一项是由 2020 个连续的数字 9 组成的:

\[ 9 + {99} + {999} + {9999} + \cdots + \underset{{2019}\text{ 个九 }}{\underbrace{{99}\ldots 9}} + \underset{{2020}\text{ 个九 }}{\underbrace{{99}\ldots 9}} \]

请问数字 1 在答案中重复出现了几次?

Alex writes down the value of the following sum, where the final term is the number consisting of 2020 consecutive nines:

\[ 9 + {99} + {999} + {9999} + \cdots + \underset{{2019}\text{ nines }}{\underbrace{{99}\ldots 9}} + \underset{{2020}\text{ nines }}{\underbrace{{99}\ldots 9}} \]

How many times does the digit 1 appear in the answer?

问题 26-30 的答案为 000-999 之间的整数, 请将答案填在答案卡上对应的位置。

第 26 题占 6 分, 第 27 题占 7 分, 第 28 题占 8 分, 第 29 题占 9 分,第 30 题占 10 分。

For questions 26 to 30, shade the answer as an integer from 0 to 999 in the space provided on the answer sheet.

Questions 26-30 are worth 6, 7, 8, 9 and 10 marks, respectively. 26. 若 \( n \) 是一个正整数,定义 \( n \) ! 为从 1 到 \( n \) 所有整数的积。例如, \( 4! = 4 \times 3 \times 2 \times 1 = \) 24。请问算式 \( 1! + 2! + 3! + \ldots + {2020}! \) 的结果最右侧的三位数字是什么？

If \( n \) is a positive integer, \( n \) ! nd by multiplying the integers from 1 to \( n \) . For example, \( 4! = 4 \times 3 \times 2 \times 1 = {24} \) .

What are the three rightmost digits of the sum \( 1! + 2! + 3! + \cdots + {2020}! \) ?

27.

一个边长为 \( {10}\mathrm{\;{cm}} \) 的正方形放置在一条直线上。点 \( P \) 是这个正方形初始时位于左下方的一个顶点, 如图所示。将正方形沿着这条直线按照顺时针的方向滚动直到点 \( P \) 再次回到这条直线上为止。请问点 \( P \) 的运动轨迹与直线形成的区域面积最接近多少 \( {\mathrm{{cm}}}^{2} \) ？

A square of side length \( {10}\mathrm{\;{cm}} \) is sitting on a line. Point \( P \) is the corner of the square which starts at the bottom left, as shown. Without slipping, the square is rolled along the line in a clockwise direction until \( P \) returns to the line for the first time. To the nearest square centimetre, what is the area under the curve traced by \( P \) ?

28.

三条边长分别为 \( {30}\mathrm{\;{cm}} \) 、 \( {40}\mathrm{\;{cm}} \) 与 \( {50}\mathrm{\;{cm}} \) 的八个直角三角形, 依照如图所示的方式放置。

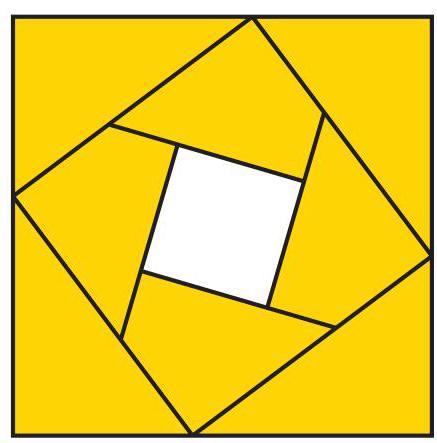
内部的四个三角形互相重叠在一起, 但外部的四个三角形则互不重叠。

请问中间未涂色正方形的面积为多少 \( {\mathrm{{cm}}}^{2} \) ？

Eight identical right-angled triangles with side lengths \( {30}\mathrm{\;{cm}},{40}\mathrm{\;{cm}} \) and \( {50}\mathrm{\;{cm}} \) are arranged as shown.

The inner four triangles are made to overlap each other, but the outer four triangles do not overlap any of the others.

What is the area, in square centimetres, of the unshaded centre square?

29.

我将 16 片正方形碎布缝合在一起制作一个 \( 4 \times 4 \) 的方格表挂饰, 碎布颜色分为红色、蓝色、绿色、黄色四种, 要求同颜色的碎布不可以接触, 包括顶点。

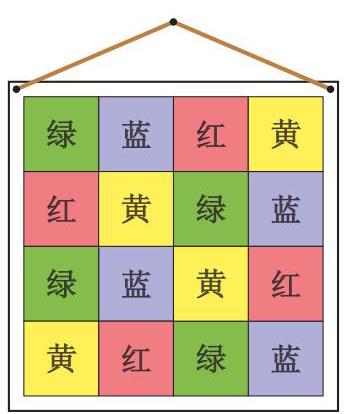
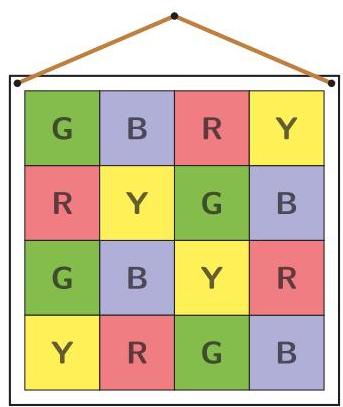
右图是一个失败的试验品, 因为两片黄色碎布的顶点有接触。

请问我总共有多少种不同的方法可以正确排列这些碎布?

My grandson makes wall hangings by stitching together 16 square patches of fabric into a \( 4 \times 4 \) grid. I asked him to use patches of red, blue, green and yellow, but to ensure that no patch touches another of the same colour, not even diagonally.

The picture shows an attempt which fails only because two yellow patches touch diagonally.

In how many different ways can my grandson choose to arrange the coloured patches correctly?

30.

有一个十二小时制的时钟,它的时针与分针的长度相同。这个时钟上有一个不确定的时刻是指您无法判断正确的时间,因为在 12 小时区间里两针会有两次指向相同的位置。

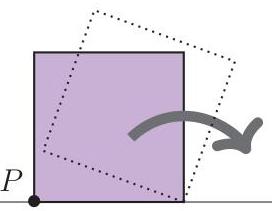
例如, 右图时钟显示的时刻可以看成下午 7: 23 或者下午 4: 37, 所以这一刻的时间是不确定的。然而, 下午12: 00 是确定的, 因为此刻时针和分针是重叠在一起的。

请问从中午到午夜这 12 小时内,总共会出现几个不确定的时刻?

A clockmaker makes a 12-hour clock but with the hour and minute hands identical. An ambiguous time on this clock is one where you cannot tell what time it is, since the exact position of the two hands occurs twice in a 12-hour cycle.

For instance, the clock shown can be seen at approximately \( {7.23}\mathrm{{pm}} \) and \( {4.37}\mathrm{{pm}} \) so both of these times are ambiguous. However, \( {12.00}\mathrm{{pm}} \) is not ambiguous, since both hands are together.

How many ambiguous times happen in the 12 hours from midday to midnight?