澳大利亚AMC-10年级D

小学中段解答

逐行计数，共有\( 3 + 4 + 5 + 5 + 5 = {22} \)个点，hence (C).

方案二

再添3个点就构成一个\( 5 \times 5 \)的正方形，共25个点，因此图案中有\( {25} - 3 = {22} \)个点，

故选(C)。

故选(D)。

故选(B)。

故选(B)。

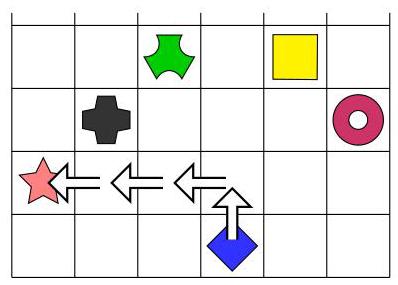
他最终落在标记为

故选(A)。

然而，图中没有正方形，

故选(D)。

因此选(E)。

因此选(B)。

因此选(A)。

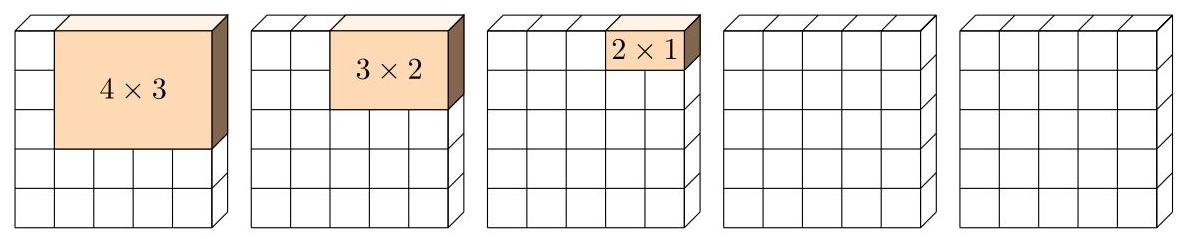
缺失立方体的总数为\( {12} + 6 + 2 = {20} \)，

因此选(E)。

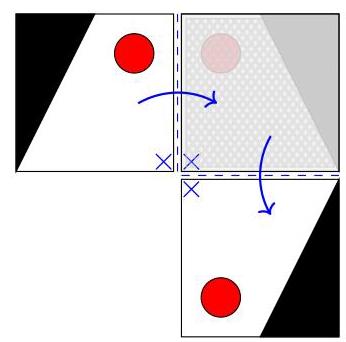
特别是，右下角(标记为\( \times \))保持不动，最终出现在左上角。只有(A)满足这一点，

因此选(A)。

依次测试每个数字，我们发现

(A) \( 7 + 1 = 8 \) 但 \( {11} - 1 = {10} \)

(B) \( 7 + 2 = 9 \) 且 \( {11} - 2 = 9 \) ✓

(C) \( 7 + 3 = {10} \) 但 \( {11} - 3 = 8 \)

(D) \( 7 + 4 = {11} \) 但 \( {11} - 4 = 7 \)

(E) \( 7 + 5 = {12} \) 但 \( {11} - 5 = 6 \)

因此，在所有可选项中，只有数字2可以填入方框使该数式成立，故选(B)。

解法2

在所示数轴上，\( 7 + \square \) 和 \( {11} - \square \) 最终都落在同一点:

两次跳跃都到达9，位于7和11的正中间。于是 \( \square \)，即每次跳跃的长度，为2个单位，故选(B)。

故选(B)。

覆盖整个十字形所需瓷砖总数即为 \( 5 \times 8 = {40} \)，

故选(E)。

如果我们用\( 2 \times 6 \)得到12，就必须用\( 4 + 7 \)得到11。这样剩下1、3和5，没有哪一对相减能得到1。

于是我们尝试\( 3 \times 4 = {12} \)和\( 5 + 6 = {11} \)，剩下1、2和7。此时\( 2 - 1 = 1 \)，因此未使用的卡片是7，

故选(E)。

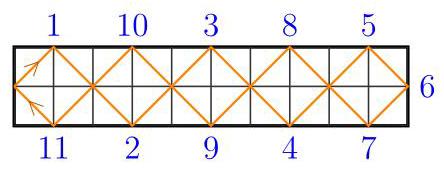
如编号所示，光束在镜子上反射了11次，故选(D)。

故选(C)。

下表显示每次存款后的余额:

周	哈米什	伊丽莎
1	12	32
2		36
3	24	40
4		44
5	36	48
6		52
7	48	56
8		60
9	60	64
10		68
11	72	72

因此选(E)。

方案2

第1周存款后，Eliza的银行账户比Hamish多20美元。

两周后(第3周)，Hamish又存了\( \$ {12} \)，Eliza又存了\( \$ 8 \)，两人账户差额减少了\( \$ 4 \)。

再过两周，两人账户差额又减少了4美元。

如此继续，直到账户差额总共减少了\( 5 \times 4 = {20} \)美元，这发生在第1周之后的\( 5 \times 2 = {10} \)周，即第11周，

因此选(E)。

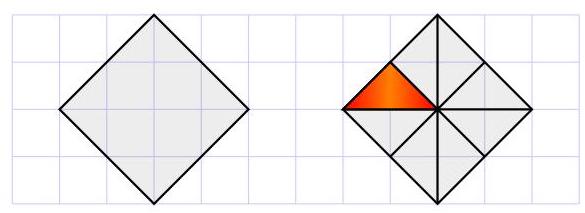
下一个最小的集合是1、2、3和5，但同样出现上述问题。在这两种情况下，我们都无法使用1、2和3，因为第一张图表明一旦放置了1和2，就无法再放置3。

下一个最小的总和由1、2、4和5组成，其和为12。第二张图显示这种组合可行，因此选(C)。

从这些数中，我们需要选出三个数使其和为21。先选最大的数，再确定其余两个数。例如，若选14，则其余两数之和为7，只能是5+2。按此方法，我们共找到四种组合使三数之和为21:

三个数			和	积
14	5	2	21	140
10	10	1	21	100
10	7	4	21	280 ✓
7	7	7	21	343

唯一能得到乘积280的解是当这三个数为4、7和10时，

因此选(C)。

展开图(A)到(E)中没有任何一个将这两个面直接相连，因此这两个被穿孔的面必须是像下图那样在一条公共边上才最终相连的两个面:

以下是五个展开图，箭头标示了某些边如何连接以构成立方体。对于每个展开图，两个被刺穿面之间的连接用实心箭头表示，连接后的面显示在下方:

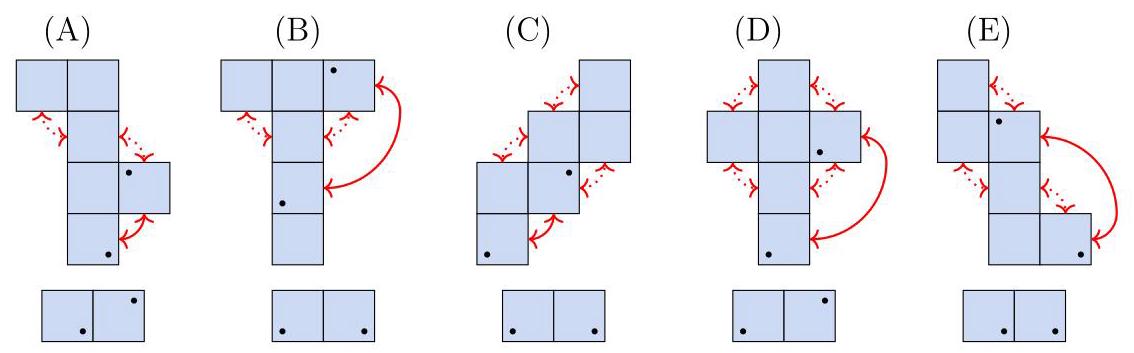
在这些图中，只有(D)的两个穿孔面的朝向正确，因此选(D)。

我们不能仅仅增加个位数，因为所有大于4的数字都已经被用过了。

增加十位或百位数字时也是如此。因此，我们必须增加千位数字。

最小的改动是把这一位增加到7，然后在接下来的三位使用尽可能小的数字。这样就得到897012，因此还需要258个单位，于是记作(258)。

从2开头的数开始，这些包含数字3的数有:203、213、223、230、231、232、233、234、235、236、237、238、239、243、253、263、273、283、293，共19个。同样，以4开头且包含数字3的数也有19个。最后，从300到399的所有100个数都包含数字3。综上，从200到500之间共有\( {19} + {100} + {19} = {138} \)个数包含数字3，因此结果为138。

方案2

由于500不含数字3，我们可以把注意力放在200到499这300个数上。我们先统计其中不含数字3的数。三个数位上的可选数字如下:

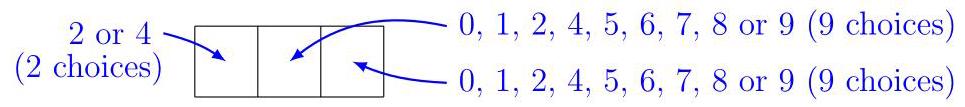
这些\( 2 \times 9 \times 9 = {162} \)选择中的任何一种都会给出一个介于200到499之间且不含数字3的数。那么就有\( {300} - {162} = {138} \)个数\( {do} \)含有数字3，

因此(138)。

为了补偿，我们至少需要另一个数字，其使用的段数多于自身数值，即0、1、2或3。最大的增益来自使用0，它比自身数值多用了6段。使用9和0时，数字之和比所用段数少3。这允许我们再使用一个9来平衡两个总和。因此990就是这样的数，且更大的数都不行，

故(990)。

29.(亦UP26)

Nguyen的序列以1、6、16、36、76开始。第六个数应为156，但由于他不写百位数字，因此写作56。同理，第七个数是16，与第三个数相同。此后数字按四个数循环:\( {16},{36},{76},{56}\ldots \)于是每一项都与前四项相同，因此第2022个数将与第6个数相同，即56，

故(56)。

可供选择的数字是1到105之间的所有奇数。

因此最小可能和为\( 1 + 3 + 5 = 9 \)，最大为\( {101} + {103} + {105} = {309} \)，且任意三个奇数之和必为奇数。

从9到309之间的每一个奇数均可实现，方法是从\( 1 + 3 + 5 = 9 \)开始，按如下模式每次增加2:

\[ 1 + 3 + 5 = 9\;1 + 3 + 7 = {11}\;1 + 5 + 7 = {13} \]

\[ 3 + 5 + 7 = {15}\;3 + 5 + 9 = {17}\;3 + 7 + 9 = {19} \]

\[ {99} + {101} + {103} = {303}\;{99} + {101} + {105} = {305}\;{99} + {103} + {105} = {307} \]

\[ {101} + {103} + {105} = {309} \]

此表共有50整行，因此共有\( 3 \times {50} + 1 = {151} \)种可能的总和，

故(151)。

高小解答

二十万五千一百五十写作205150，

故(E)。

共有9个大小相同的小正方形，其中4个被涂色，因此分数为\( \frac{4}{9} \)，

故(D)。

\( {2220} - {2022} = {198}, \)

故选(C)。

故选(B)。

故选(C)。

解法1

在29个正方形中，有12个正方形有3条边位于周长上，4个正方形有2条对边位于周长上，4个正方形有2条邻边位于周长上。这已涵盖该图形全部\( {12} \times 3 + 4 \times 2 + 4 \times 2 = {52} \)条边，

故选(A)。

解法2

从中心的\( 3 \times 3 \)正方形开始，其周长为\( P = {12} \)。依次连接其余20个正方形。每次连接使\( P \)增加2:新正方形带来4的增加，但连接又减少2。连接完20个正方形后，\( P = {12} + {20} \times 2 = {52} \)，

故选(A)。

故选(E)。

因此选(C)。

因此选(E)。

我们寻找红色区域数量是白色区域两倍的转盘。第四个转盘有4个红色区域和2个白色区域，是唯一符合条件的，因此选(D)。

因此选(E)。

因此选(D)。

因此选(C)。

因此选(D)。

因此(A)。

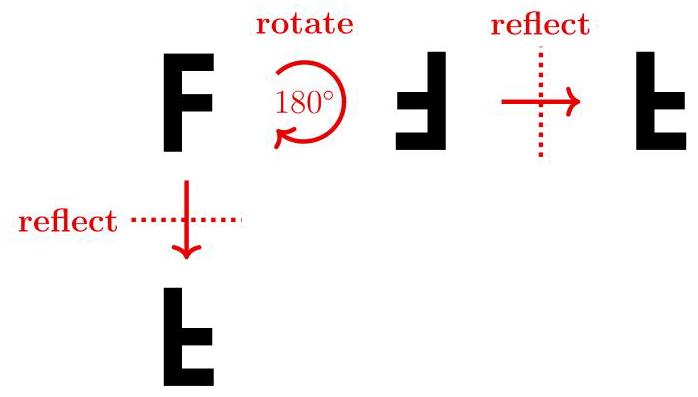
因此，一个字母经过此操作后仍保持不变，它必须具有水平对称轴。这样的字母共有9个:

因此(E)。

因此(B)。

因此(A)。

解法一

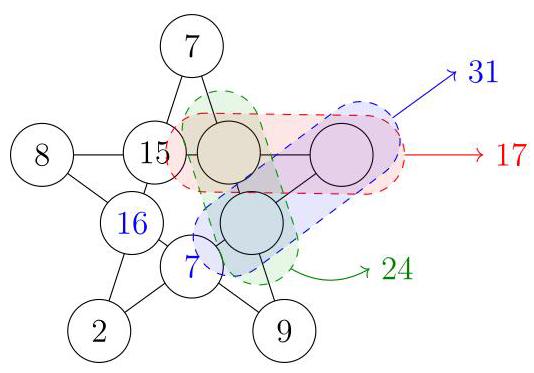
通过7和2的直线目前已有\( 7 + {15} + 2 = {24} \)，因此缺失的数字是\( {40} - {24} = {16} \)。同理，通过8和9的直线已有\( 8 + {16} + 9 = {33} \)，缺失的数字是\( {40} - {33} = 7 \)。还有三条直线待完成。每条中已知两个数字，因此可确定另外两个数字之和，如图所示。

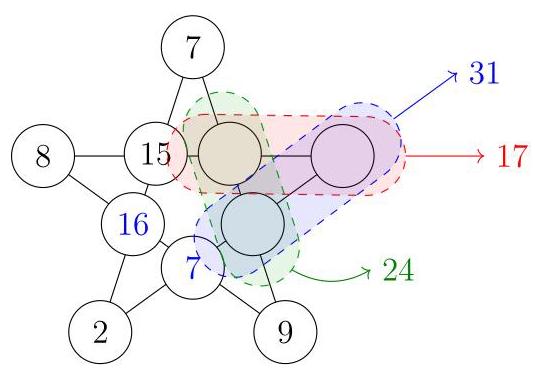
将\( {31} + {17} + {24} = {72} \)相加时，每个未知数字被计算了两次。因此这三个未知数字之和为36。

这意味着这三个未知数字是\( {36} - {31} = 5,{36} - {17} = {19} \)和\( {36} - {24} = {12} \)。在已用的十个数字中，最大的就是刚找到的19，

因此选(E)。

方法二

因此选(E)。

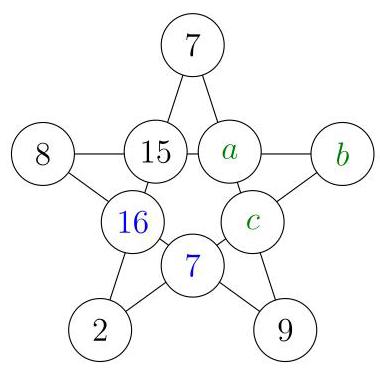
补全\( 7 + {15} + x + 2 = {40} \)得到\( x = {16} \)，如图所示。

补全\( 8 + {16} + y + 9 = {40} \)得到\( y = 7 \)，如图所示。

每行之和为40，因此5行总和为\( 5 \times {40} = {200} \)。这相当于每个数被计算了两次，所以10个数之和为100。

已知7个数之和为64，因此\( a + b + c = {36} \)。由于\( a + b = {17}, c = {36} - {17} = {19} \)。现在可求出最后两个数:\( a = 5 \)和\( b = {12} \)。

使用的最大数为\( c = {19} \)，

26.(亦见MP29)

Nguyen的数列以1,6,16,36,76开始。第六个数应为156，但他不写百位数字，于是记为56。同理，第七个数是16，与第三个数相同。此后数字按四个数\( {16},{36},{76},{56}\ldots \)循环出现。因此每一项都与前四项相同，第2022个数将与第6个数相同，即56，

因此答案为(56)。

因此答案为(405)。

可供选择的数为1到105之间的所有奇数。

因此最小可能和为\( 1 + 3 + 5 = 9 \)，最大为\( {101} + {103} + {105} = {309} \)，且三个奇数之和必为奇数。

从\( 1 + 3 + 5 = 9 \)开始，按每次增加2的规律递增，9到309之间的所有奇数均可实现:

\[ {101} + {103} + {105} = {309} \]

此表共有50个完整行，因此共有\( 3 \times {50} + 1 = {151} \)种可能的总和，

因此(151)。

因此(150)。

在网络上，我们可以识别人脸并可视化它们如何折叠在一起:

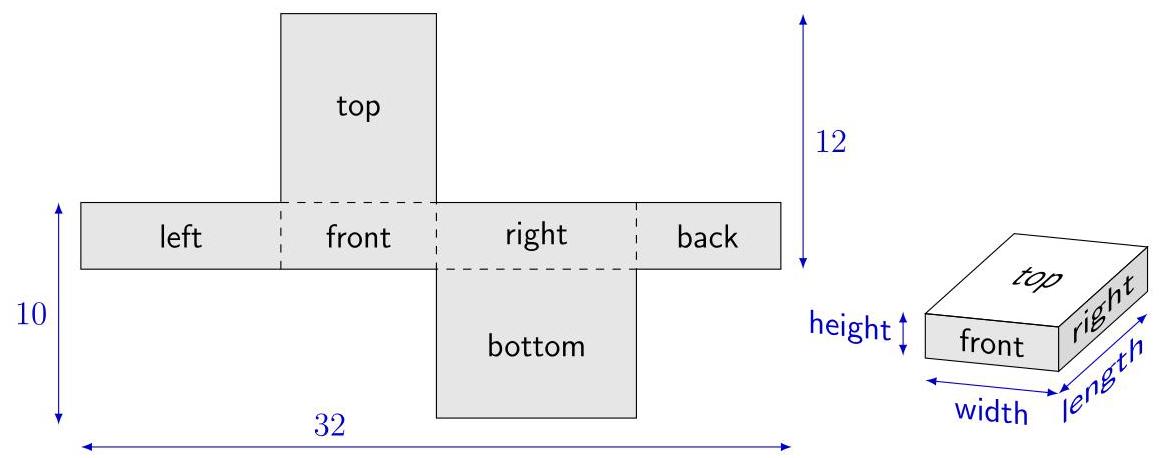
将高度设为2。从前视图和俯视图来看，棱柱的长度为\( {12} - 2 = {10} \)。同样，从右视图和底视图来看，棱柱的宽度为\( {10} - 2 = 8 \)。因此，展开图的总宽度为\( 2 \times 8 + 2 \times {10} = {36} \)，但它应为32。

随着高度增加，计算出的宽度和长度都会变小。因此尝试3。此时宽度为\( {10} - 3 = 7 \)，高度为\( {12} - 3 = 9 \)。由此，网的总宽度为\( 2 \times 7 + 2 \times 9 = {32} \)。

若继续增加高度，网将变得比\( {32}\mathrm{\;{cm}} \)更窄。

因此，棱柱的体积为\( 9 \times 7 \times 3 = {189}{\mathrm{\;{cm}}}^{3} \)，

因此(189)。

方案2

在网络上，我们可以识别人脸并可视化它们如何折叠在一起，用\( L, W \)和\( H \)标记每条边:

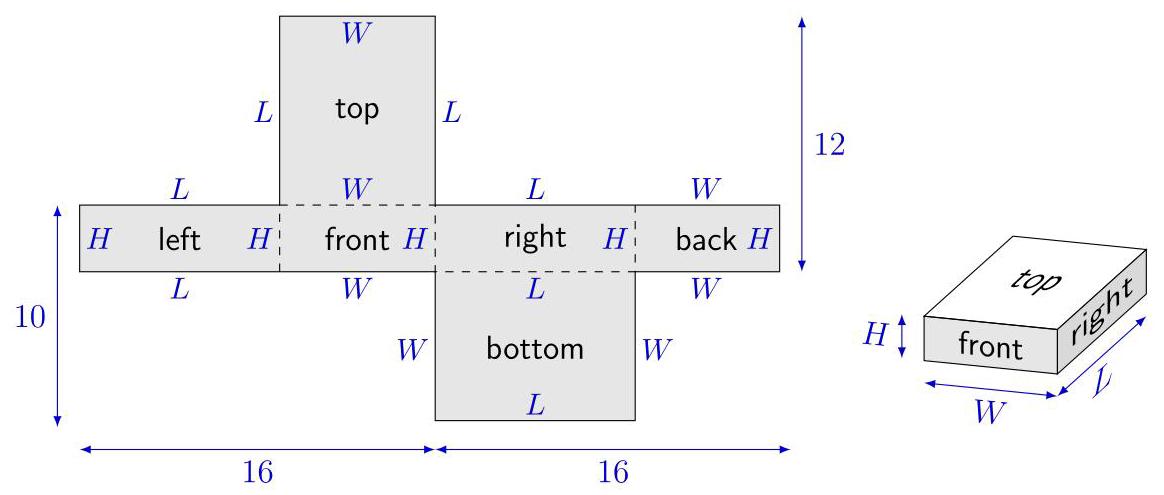
比较图中的12和10，\( L \)比\( W \)多2。

将32拆成两个16，如所示，\( L + W \)必须是16。唯一满足\( L \)比\( W \)大2的和\( L + W = {16} \)是\( 9 + 7 = {16} \)。也就是说，\( L = 9 \)和\( W = 7 \)。于是\( H = {10} - 7 = 3 \)。

对照原图检查，\( W + H = 7 + 3 = {10}, L + H = 9 + 3 = {12} \) 和 \( L + W + L + W = 9 + 7 + 9 + 7 = {32}. \)

盒子的体积为 \( 9 \times 7 \times 3 = {189}{\mathrm{\;{cm}}}^{3} \)，因此选 (189)。

初级解答

因此选 (E)。

\( 4 - 7 = - 3 \)

因此选 (C)。

因此选 (B)。

我们寻找红色区域数量是白色区域两倍的转盘。第四个转盘有 4 个红色区域和 2 个白色区域，是唯一符合条件的，

因此选 (D)。

正方形面积为 \( 2 \times 2 = 4 \)。阴影三角形面积为 \( \frac{1}{2} \times 1 \times 2 = 1 \)。因此阴影三角形占总面积的 \( \frac{1}{4} \)，故选 (B)。

解法二

正方形可分成 4 个与阴影三角形全等的部分，因此阴影三角形占总面积的 \( \frac{1}{4} \)，故选 (B)。

因此选(E)。

化为带分数，\( \frac{7}{2} = 3\frac{1}{2},\frac{15}{4} = 3\frac{3}{4},\frac{16}{5} = 3\frac{1}{5},\frac{17}{4} = 4\frac{1}{4} \) 和 \( \frac{18}{5} = 3\frac{3}{5} \) 。其中只有 \( 4\frac{1}{4} \) 介于4与5之间，因此选(D)。

解法二

无需将这些分数化为带分数，注意到它们大多小于 \( 4 = \frac{8}{2} = \frac{16}{4} = \frac{20}{5} \) 。唯一大于4的是 \( \frac{17}{4} = 4\frac{1}{4} \) ，且其小于5，

因此选(D)。

因为 \( \bigtriangleup {PQR} \) 是等腰三角形，所以 \( \angle {PQR} = \angle {PRQ} \) 。又 \( \angle {PQR} + \angle {PRQ} = {180}^{ \circ } - {48}^{ \circ } = {132}^{ \circ } \) 。于是 \( \angle {PQR} = \angle {PRQ} = {132} \div 2 = {66}^{ \circ } \) ，

因此选(B)。

于是向前数2天到周二正午，再回退6小时到周二上午6点，因此选(A)。

因此选(C)。

因此选(C)。

澳大利亚需要再购买足够使用30天的汽油。这相当于\( {30} \times {160} \)百万\( = {4800} \)百万升，

因此选(E)。

因此选(C)。

\( N \)	1	12	123	1234	12345	123456	1234567	12345678	123456789
\( S \)	1	3	6	10	15	21	28	36	45
÷3？	✘	✓	✓	✘	✓	✓	✘	✓	✓

因此，这些数中有6个能被3整除，故选(D)。

因此，最少需要7颗骰子才能看到100个点，故选(C)。

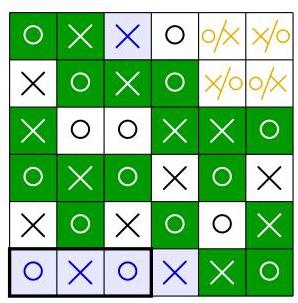
由于每列每行必须各有三个符号，五个浅色背景的符号是必需的。剩下的四个格子有两种填法，如金色所示。然而，在这两种情况下，三个加框的格子都是\( \circ \times \circ \)，

故选(B)。

19. 解法一

假设Ash与Sash交换\( x \)张牌，Ash与Tash交换\( y \)张牌，Sash与Tash交换\( z \)张牌。那么Ash的总牌数给出\( x + y = {11} \)，Sash给出\( x + z = 8 \)，Tash给出\( y + z = {15} \)。将三个方程相加得\( {2x} + {2y} + {2z} = {11} + 8 + {15} = {34} \)，于是\( x + y + z = {17} \)。用第一个方程相减得\( z = 6 \)，

故选(D)。

解法二

共有\( 8 + {11} + {15} = {34} \)张牌。Ash给出11张又收回11张，因此他接触了22张牌，未接触\( {34} - {22} = {12} \)张牌。这12张牌必须在Sash与Tash之间交换，而每次交换涉及2张牌，故Sash与Tash之间共有6次交换。于是，在Sash的8次交换中，\( 8 - 6 = 2 \)次是与Ash进行。同理，Tash与Ash交换\( {15} - 6 = 9 \)张牌。这些数值给出完整解，确认唯一解为Sash与Tash交换6张牌，故选(D)。

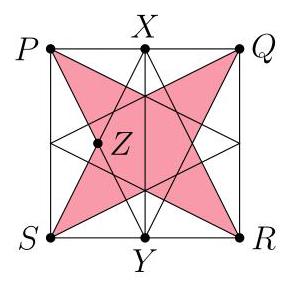
设\( X, Y \)和\( Z \)如图中所示，并画出直线\( {XY} \)。由对称性，点\( Z \)是矩形\( {PXYS} \)的中心。因此\( \bigtriangleup {SZP} \)的面积是该矩形面积的\( \frac{1}{4} \)，从而也是\( {PQRS} \)面积的\( \frac{1}{8} \)。共有四个这样的未阴影三角形，所以\( {PQRS} \)的未阴影面积为\( 4 \times \frac{1}{8} = \frac{1}{2} \)，于是阴影部分所占比例也是\( \frac{1}{2} \)，

故选(D)。

解法二

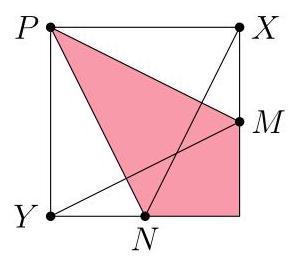
因此选(D)。

仅考虑正方形的一个象限，标记如图所示。第6题(见第??页)的解答表明，三角形\( {PYN} \)和\( {PXM} \)的面积各为这个较小正方形的\( \frac{1}{4} \)，因此剩余阴影区域的面积是这个正方形的\( \frac{1}{2} \)。这一结论适用于大正方形\( {PQRS} \)的每一个象限，所以整个正方形有\( \frac{1}{2} \)的面积被阴影覆盖。

此后，数字在169和256之间交替出现，奇数位为169，偶数位为256。因此，第2022项将是256，

因此(C)。

因此，第105列中阴影方格的数量等于105的因数个数。105的因数为\( \{ 1,3,5,7,{15},{21},{35},{105}\} \)，所以第105列有8个阴影方格，

因此(C)。

因此(C)。

24. 备选方案1

\( \frac{1}{2} - \frac{1}{3} = \frac{1}{6} > \frac{1}{10} \) 因此\( \frac{1}{2} \)减去任何较小的分数后仍大于\( \frac{1}{10} \)。这给出了7对。

如果较大的分数是\( \frac{1}{3} \)，那么\( \frac{1}{3} - \frac{1}{4} = \frac{1}{12} < \frac{1}{10} \)但\( \frac{1}{3} - \frac{1}{5} = \frac{2}{15} > \frac{1}{10} \)。较小的分数同样适用，还会产生另外5对。

如果较大的分数是\( \frac{1}{4} \)，那么我们必须到达\( \frac{1}{4} - \frac{1}{7} \)才能找到一对差值大于\( \frac{1}{10} \)的分数。较小的分数同样适用，还会再给出3对。

若较大分数小于或等于\( \frac{1}{5} \)，则减去任何较小分数所得结果均小于\( \frac{1}{10} \)，因此不存在更多数对。

总共有\( 7 + 5 + 3 = {15} \)对，

因此选(C)。

替代方案2

制作一张表格，将每个分数保留三位小数，把差值大于0.1的单元格标出阴影。由于存在递增和递减趋势，无需计算所有差值。

第二个分数

第一分数		0.333	0.250	0.200	0.167	0.143	0.125	0.111
	0.500	0.167
	0.333	-	0.083	0.133
	0.250	-	-		0.083	0.107
	0.200	-	-	-				0.089

这些差异可能是由于四舍五入误差造成的，但这种情况只能出现在千分位，因此毫无疑问，其中有15个差异大于0.1，

故选(C)。

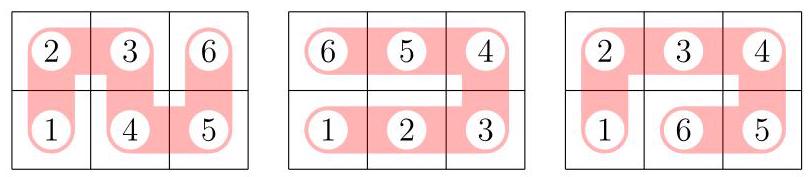
四个角落情况相同，共产生12种放置方式。

若从中心格开始，则仅有两种可能:

两个中心格情况相同，共产生4种放置方式。

总计共有\( {12} + 4 = {16} \)种放置方式，故选(A)。

显然\( \heartsuit \)不能为0，否则所得和\( \heartsuit \heartsuit \diamondsuit \)将小于被加数。因此\( \heartsuit \)为9，从而\( \diamondsuit \)为4。

为确保个位产生进位，\( \square \)必须为7。于是和为\( {497} + {497} = {994} \)，且\( \diamondsuit \heartsuit \square = {497} \)，

27. 解法一

设这两个数分别为abcd和efgh，则两数之和为

\[ {1000}\left( {a + e}\right) + {100}\left( {b + f}\right) + {10}\left( {c + g}\right) + \left( {d + h}\right) \]

若加法过程中无进位，则该和的各位数字依次为\( a + e \)、\( b + f, c + g \)和\( d + h \)，其数字和为\( a + e + b + f + c + g + d + h = {36} \)。例如\( {1234} + {8765} = {9999} \)无进位，其数字和为36。

在标准加法算法中，每产生一次进位，某一列的值减少10，而左侧一列增加1，因此答案中所有数字之和总共减少9。于是若出现一次、两次或三次进位，数字和将分别降至27、18或9。和不可能减至0，且存在三次进位的例子如\( {6431} + {8572} = {15003} \)，表明最小可能的数字和为9。

因此最小与最大数字和之差为\( {36} - 9 = {27} \)，

故答案为27。

方案2

设这两个四位数为\( A \)和\( B \)，并设\( C = A + B \)。\( C \)的最大可能值是\( {1000} \times \left( {8 + 7}\right) + {100} \times \left( {6 + 5}\right) + {10} \times \left( {4 + 3}\right) + \left( {2 + 1}\right) = {16173} \)。于是\( {C}^{\prime } \)，即\( C \)的各位数字之和，最多为36，当\( C = {9999} \)时取得。这个最大值可以通过多种方式得到，例如\( A = {8765}, B = {1234} \)，其\( C = {9999} \)且\( {C}^{\prime } = {36} \)。

为了找到最小的\( {C}^{\prime } \)，我们可以尝试在\( A \)和\( B \)中配对数字，使得\( C \)的大部分数字为0。例如，若\( A = {5876} \)且\( B = {3124} \)，则\( C = {9000} \)且\( {C}^{\prime } = 9 \)。这似乎就是最小可能值。

我们断言\( {C}^{\prime } \)是9的倍数，这将确认\( {C}^{\prime } \)至少为9。这可以用通常称为“去九法”的标准9整除检验原理来证明。

设\( {A}^{\prime } \)为\( A \)的各位数字之和，\( {B}^{\prime } \)为\( B \)的各位数字之和。则\( {A}^{\prime } + {B}^{\prime } = \)\( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = {36} \)，它是9的倍数。\( A \)和\( {A}^{\prime } \)除以9的余数始终相同，因此\( A - {A}^{\prime } \)是9的倍数。具体而言，若\( A = {1000a} + {100b} + {10c} + d \)且\( {A}^{\prime } = a + b + c + d \)，则\( A - {A}^{\prime } = 9\left( {{111a} + {11b} + c}\right) \)。同理，\( B - {B}^{\prime } \)也是9的倍数。于是

\[

\]

因此\( C \)是9的倍数，从而\( {C}^{\prime } \)也是9的倍数。如上所述，\( {C}^{\prime } \)的最小可能值为9，因此上面得到的\( {C}^{\prime } = 9 \)就是最小的数字和。于是最小与最大数字和之差为\( {36} - 9 = {27} \)，

故为27。

评注:一种表达方式是使用模运算。我们不再写“\( A - {A}^{\prime } \)是9的倍数”，而写\( A \equiv {A}^{\prime }\left( {\;\operatorname{mod}\;9}\right) \)。模运算让我们能在一行内证明关于\( {C}^{\prime } \)的断言:\( {C}^{\prime } \equiv C = A + B \equiv {A}^{\prime } + {B}^{\prime } = {36} \equiv 0\left( {\;\operatorname{mod}\;9}\right) \)。

其他行按相同步骤计算，借助列中的某些规律。此处已完整列出所有除法结果，尽管多数情况下无需如此。该策略很快结束，因为每支队伍所得超过学员金额的18倍，且至少有7支队伍，故队伍总金额超过学员金额的126倍。由于\( {126} \times 8 > {1000} \)，学员金额不超过\( \$ 7 \)。

训练师\$	护具\$	腿部\$	队伍\$	所有训练师\$	所有队伍 \$	队伍数量	确定？
2	12	17	46	40	960	\( {960} \div {46} = {20}\frac{40}{46} \)	✘
3	18	23	64	60	940	\( {940} \div {64} = {14}\frac{44}{64} \)	✘
4	24	29	82	80	920	\( {920} \div {82} = {11}\frac{18}{82} \)	✘
5	30	35	100	100	900	\( {900} \div {100} = 9 \)	是
6	36	41	115	120	880	\( {880} \div {115} = 7\frac{75}{115} \)	✘
7	42	47	136	140	860	\( {860} \div {136} = 6\frac{44}{136} \)	✘

因此唯一解为每名学员\( \$ 5 \)，共9支队伍，俱乐部共有\( {20} + 9 \times 3 = {47} \)名成员，故得(47)。

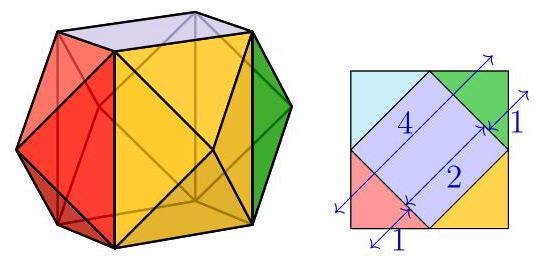
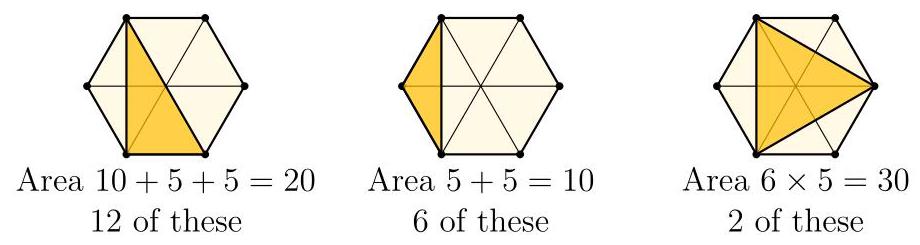
正六边形由六个面积为10的等边三角形组成，可作为测量网格。

图示为Horton测量的三种唯一不同(不全等)类型的三角形。利用网格，我们可以测量每个三角形的面积，并通过考虑旋转与反射，统计每类三角形的数量:

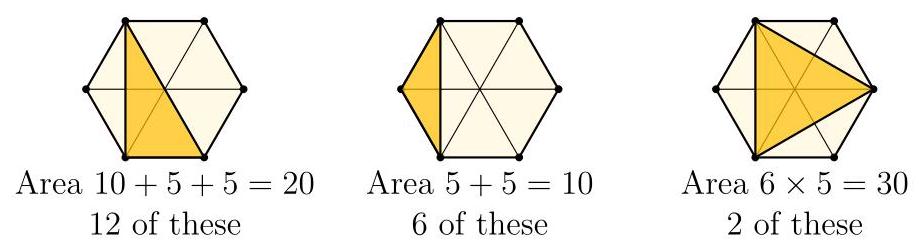
于是这20个三角形的总面积为

\[ {12} \times {20} + 6 \times {10} + 2 \times {30} = {240} + {60} + {60} = {360}, \]

故得(360)。

解法一

假设和中的三个数按递增顺序为\( x, y \)和\( z \)。

若\( x = 1 \)，则\( y \)至少为2以避免重复；另一方面，\( y \)不能大于49，否则\( z \)会更小。因此\( y \)的取值范围为2–49，共48种可能。

若\( x = 2 \)，则\( y \)至少为3以避免重复。若\( y = {49} \)，则其等于\( z \)，这是不允许的。因此\( y \)的取值范围为\( 3 - {48} \)，共46种可能。

若\( x = 3 \)，则\( y \)的取值范围为4–48，共45种可能。依此类推，得到下表所示的子总计。注意当\( x \)为奇数时，\( y \)与\( z \)必不相等，因为一奇一偶；而当\( x \)为偶数时，需小心避免\( y = z \)的情况。这解释了子总计在表中向下移动时交替递减的模式。

\( x \)	\( y \)	小计
1	2-49	48
2	3-48	46	)-2
3	4-48	45	) -1
4	5-47	43	)-2
\( \vdots \)	\( \vdots \)	\( \vdots \)	) -1
29	30-35	6
30	31-34	4	)-2
31	32-34	3	) -1
32	33	1	) -2

因此总和的总数为

\[ 1 + 3 + 4 + 6 + 7 + 9 + \cdots + {40} + {42} + {43} + {45} + {46} + {48}, \]

或

\[ 1 + 4 + 7 + \cdots + {40} + {43} + {46} \]

\[ + {48} + {45} + {42} + \cdots + 9 + 6 + 3 \]

由于表格共有32行，上述求和包含16对数字，每对之和为49，因此总和为\( {49} \times {16} = {784} \)，即784。

解法二

每个形如\( {100} = {61} + {34} + 5 \)的和可以形象地表示为一排三种颜色的计数器，例如61个红色计数器，接着34个绿色计数器，再接着5个蓝色计数器。

我们首先计算允许某些颜色数量相等、且相同数字的不同排列(颜色)分别计数的计数器排列总数。此时，每一种选择对应于在上图中选取两个箭头的位置。这两个箭头位于不同位置且不在第一个计数器上，因此共有99个可选位置。

从99个位置中选取2个位置的方法数为\( {99} \times {98} \div 2 \)，因为先选一个计数器再选另一个共有\( {99} \times {98} \)种方式，但每对都被计算了两次。也就是说，共有\( {99} \times {49} = {4851} \)种方式排成红、绿、蓝计数器依次出现的行。

我们需要排除那些\( a + b + c \)的排列，其中\( a, b \)和\( c \)中有两个或更多相同。由于不可能\( a = b = c \)，我们只需排除\( a = b \)、\( a = c \)或\( b = c \)的情况。

对于\( a = b \)，有49种可能，从\( 1 + 1 + {98} \)到\( {49} + {49} + 2 \)。同理，\( a = c \)和\( b = c \)也各有49种可能。因此共有\( {99} \times {49} - 3 \times {49} = {96} \times {49} \)种排列满足\( a, b \)和\( c \)互不相同。

然而，每个\( {100} = a + b + c \)且\( a, b \)与\( c \)不同的和在此被计数了6次，对应于\( a + b + c, a + c + b, b + a + c, b + c + a, c + a + b \)和\( c + b + a \)。因此，将100写成三个正整数之和且不计顺序的方法数为\( {96} \times {49} \div 6 = {16} \times {49} = {784} \)，

即784。

www.amt.edu.au

中级解答

\( {2220} - {2022} = {198}, \)

故选(C)。2.(亦见UP6)

解法一

在29个正方形中，有12个正方形有3条边位于周长上，4个正方形有2条相对的边位于周长上，4个正方形有2条相邻的边位于周长上。这涵盖了该形状的全部\( {12} \times 3 + 4 \times 2 + 4 \times 2 = {52} \)条边，

因此选(A)。

替代方案2

从中心的\( 3 \times 3 \)正方形开始，其周长为\( P = {12} \)。逐个连接剩下的20个正方形。每次连接使\( P \)增加2:新正方形带来4的增加，但连接后又减少2。连接完20个正方形后，\( P = {12} + {20} \times 2 = {52} \)，

因此选(A)。

从21:00到00:00共180分钟。

因此总时间为218分钟，

因此选(B)。

\[ \text{4.}\frac{1 + 4}{9 + {16}} = \frac{5}{25} = \frac{1}{5}\text{,} \]

因此选(A)。

因为\( \bigtriangleup {PQR} \)是等腰的，所以\( \angle {PQR} = \angle {PRQ} \)。同时\( \angle {PQR} + \angle {PRQ} = {180}^{ \circ } - {48}^{ \circ } = {132}^{ \circ } \)。因此\( \angle {PQR} = \angle {PRQ} = {132} \div 2 = {66}^{ \circ } \)，hence (B).

矩形的面积为\( 7 \times {12} = {84} \)，阴影梯形的面积为\( \frac{7\left( {8 + {12}}\right) }{2} = {70} \)，因此阴影部分所占比例为\( \frac{70}{84} = \frac{5}{6} \)，

因此选(C)。

因此选(C)。

澳大利亚需要再购买足够使用30天的汽油。这是\( {30} \times {160} \)百万\( = {4800} \)百万升，因此选(E)。

\( {1011} - {674} = {337} \)

因此选(A)。

解法2

\[ {2022}\left( {\frac{1}{2} - \frac{1}{3}}\right) = {2022}\left( \frac{1}{6}\right) = {2022} \div 6 = {337}, \]

hence (A).

因此选(D)。

矩形的两条对角线在其两条对角线的中点相交。其中一条对角线的端点为(1,8)和(7,4)。中点通过坐标取平均求得

\[ \left( {\frac{1 + 7}{2},\frac{8 + 4}{2}}\right) = \left( {4,6}\right) \]

因此选(A)。

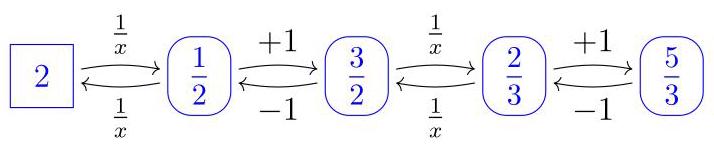
设\( x \)为所求之数。则\( \frac{5}{3} = 1 + \frac{1}{1 + \frac{1}{x}} \)，于是\( \frac{2}{3} = \frac{1}{1 + \frac{1}{x}} \)且\( \frac{3}{2} = 1 + \frac{1}{x} \)。于是\( \frac{1}{2} = \frac{1}{x} \)，从而\( x = 2 \)，因此选(C)。

解法2

该表达式由一系列“加1”与“取倒数”操作链式组成:求解时，从右到左逆向操作:因此选(C)。13. 解法1 这些角的形式为\( {2x},{3x} \)和\( {4x} \)。于是

\[ {2x} + {3x} + {4x} = {180} \]

\[ {9x} = {180} \]

\[ x = {20} \]

\[ {4x} = {80} \]

因此选(D)。

解法2

三个角分别占2、3、4份，总和为\( {180}^{ \circ } \)。因此每份为\( {180}^{ \circ } \div 9 = {20}^{ \circ } \)，最大角为\( {20}^{ \circ } \times 4 = {80}^{ \circ } \)，因此选(D)。

14. (亦见UP25)

解法一

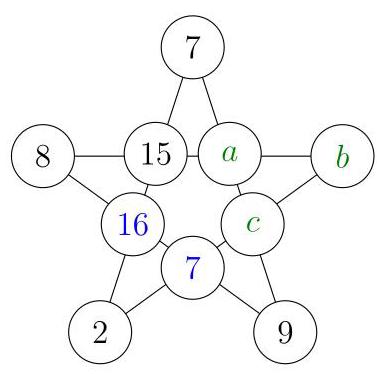
通过7和2的直线目前总和为\( 7 + {15} + 2 = {24} \)，因此缺失的数字是\( {40} - {24} = {16} \)。同理，通过8和9的直线总和为\( 8 + {16} + 9 = {33} \)，缺失的数字是\( {40} - {33} = 7 \)。还有三条直线需要完成。在每条直线中，我们已知其中两个数字，因此可以确定另外两个数字的和，如图所示。

将\( {31} + {17} + {24} = {72} \)相加时，每个未知数字被计算了两次。因此这三个未知数字的总和为36。

这意味着这三个未知数字是\( {36} - {31} = 5,{36} - {17} = {19} \)和\( {36} - {24} = {12} \)。在使用的十个数字中，最大的就是刚刚找到的19，

故选(E)。

解法二

故选(E)。

完成\( 7 + {15} + x + 2 = {40} \)后得到\( x = {16} \)，如图所示。

完成\( 8 + {16} + y + 9 = {40} \)后得到\( y = 7 \)，如图所示。

每条直线总和为40，因此将5条直线相加得\( 5 \times {40} = {200} \)。每个数字被计算了两次，所以这10个数字总和为100。

已知的7个数字总和为64，因此\( a + b + c = {36} \)。由于\( a + b = {17}, c = {36} - {17} = {19} \)。最后两个数字可求出:\( a = 5 \)和\( b = {12} \)。

使用的最大数字是\( c = {19} \)，

故选(D)。

因此选(C)。

因此选(D)。

\[ R = {5N} - {56} = {2N} - 2 \]

\[ {3N} = {54} \]

\[ N = {18}\text{ and }R = 2 \times {18} - 2 = {34} \]

于是\( R + N = {18} + {34} = {52} \)，

因此选(D)。

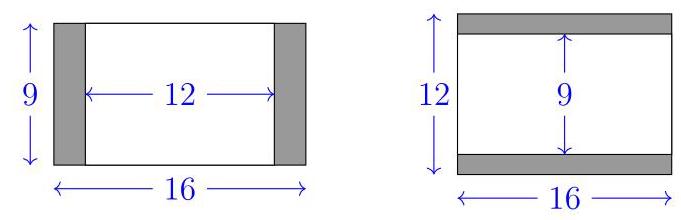
同理，右图中可设屏幕宽16单位、高12单位，未阴影部分宽16单位、高9单位。则未被遮挡的比例为\( \frac{9}{12} = \frac{3}{4} \)，故

\[ r = \frac{1}{4} \]

因此\( \ell = r \)，于是\( \ell : r = 1 : 1 \)，

按图所示标记点，其中\( M \)为\( {BC} \)的中点。由毕达哥拉斯定理，\( {PB} = {PC} = \sqrt{{8}^{2} + {1}^{2}} = \)\( \sqrt{65} \)。

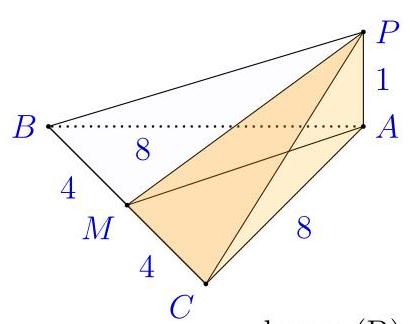
因此选(B)。

因\( \bigtriangleup {PBC} \)为等腰，\( \bigtriangleup {PMC} \)在\( M \)处为直角，

于是\( {MP} = \sqrt{{\left( \sqrt{65}\right) }^{2} - {4}^{2}} = \sqrt{49} = 7 \)。

则\( \bigtriangleup {PBC} \)的底为\( {BC} = 8 \)，高为\( {MP} = 7 \)，面积为\( \frac{1}{2} \times 8 \times 7 = {28} \)，

\[ \sqrt[3]{\frac{\left( {1 \times 2 \times 4}\right) + \left( {2 \times 4 \times 8}\right) + \cdots + \left( {n \times {2n} \times {4n}}\right) }{\left( {1 \times 3 \times 9}\right) + \left( {2 \times 6 \times {18}}\right) + \cdots + \left( {n \times {3n} \times {9n}}\right) }} \]

\[ = \sqrt[3]{\frac{8\left( {1 + 8 + \cdots + {n}^{3}}\right) }{{27}\left( {1 + 8 + \cdots + {n}^{3}}\right) }} = \sqrt[3]{\frac{8}{27}} = \frac{2}{3} \]

因此选(B)。

设桶的容量为\( {12x} \)升。则最初有\( {5x} \)升水和\( {7x} \)升牛奶。当\( 9\mathrm{\;L} \)被倒出时，其比例仍为\( 5 : 7 \)，因此倒出了\( 9 \times \frac{5}{12} = {3.75}\mathrm{\;L} \)升水和\( 9 \times \frac{7}{12} = {5.25}\mathrm{\;L} \)升牛奶。

此时剩余\( {5x} - {3.75}\mathrm{\;L} \)升水和\( {7x} - {5.25}\mathrm{\;L} \)升牛奶。重新加满后，水量升至\( {5x} - {3.75} + 9 = {5x} + {5.25}\mathrm{\;L} \)。新的比例告诉我们:

\[ 7\left( {{5x} + {5.25}}\right) = 9\left( {{7x} - {5.25}}\right) \]

\[ {35x} + {36.75} = {63x} - {47.25} \]

\[ {84} = {28x} \]

\[ x = 3 \]

因此最初桶中的牛奶量为\( {7x} = {21}\mathrm{\;L} \)，

故选(B)。解法二

桶中牛奶量从\( \frac{7}{12} \)桶变为\( \frac{7}{16} \)桶。于是\( \frac{7}{16} \div \frac{7}{12} = \)\( \frac{12}{16} = \frac{3}{4} \)，即保留了四分之三的牛奶，倒出了四分之一。

倒出的9升混合液中含有\( \frac{7}{12} \times 9 = \frac{21}{4} \)升牛奶。由于这是牛奶总量的四分之一，因此桶中原有21升牛奶，

故选(B)。

故选(D)。

\[ \text{(abde)}\left( \text{bcef}\right) = \left( \text{abc}\right) \left( \text{def}\right) \text{be} \]

\[ 4 = {be} \]

\( a \)	\( b \)	\( C \)
\( d \)	\( e \)	\( f \)
\( g \)	\( h \)	\( i \)

同样\( {eh} = 4 \)。因此\( {16} = \left( {be}\right) \left( {eh}\right) = \left( {beh}\right) e = e \)，

因此选(E)。

在百位上，\( c + a \) 只能是 9 或 10。在个位上，\( b + c \) 只能是 2 或 12。若 \( b + c = 2 \)，则 \( b = c = 1 \)，进而 \( a = 1 \) 位于十位。然而，这会使 \( 1 + 1 = 2 \) 出现在百位。因此，不存在 \( b + c = 2 \) 的解。

于是\( b + c = {12} \)，接着在十位上是\( a + b = {11} \)，百位上是\( c + a = 9 \)。把它们组合起来，\( {11} + 9 - {12} = \left( {a + b}\right) + \left( {a + c}\right) - \left( {b + c}\right) = {2a} \)，因此\( {2a} = 8 \)且\( a = 4 \)。然后\( b = 7 \)且\( c = 5 \)，这个三位数\( {abc} \)就是475，

因此(475)。

方案2

按位值写出这些数字，

\[ {2022} = \left( {{1000} + {100c} + {10a} + b}\right) + \left( {{100a} + {10b} + c}\right) \]

\[ = {1000} + {110a} + {11b} + {101c} \]

\[ \Rightarrow {1022} = {110a} + {11b} + {101c} \]

那么\( {110a},{11b},{99c} \)和\( {1023} = {11} \times {93} \)都是11的倍数，可以全部移到等式左边

\[ {1023} - {110a} - {11b} - {99c} = 1 + {2c} \]

因此\( {2c} + 1 \)是11的倍数。同时\( 3 \leq {2c} + 1 \leq {19} \)，从而\( {2c} + 1 = {11} \)且\( c = 5 \)。于是\( {11}\left( {{93} - {10a} - b - {9c}}\right) = {11} \)，因此\( {10a} + b = {92} - {9c} = {92} - {45} = {47} \)。故\( a = 4 \)且\( b = 7 \)，而数\( {abc} \)为475，

因此(475)。

\[ {171} \times \underset{{111}\text{ sixes }}{\underbrace{{66}\ldots 6}} = {171} \times \frac{6}{9} \times \left( {{10}^{111} - 1}\right) \]

\[ = {114} \times \left( {{10}^{111} - 1}\right) \]

\[ = {113}\underset{{108}\text{ nines }}{\underbrace{{99}\ldots 9}}{886}. \]

因此，\( 1 + 8 + 1 + 8 + 3 + 6 + 9 \times {108} = 9 \times {111} = {999} \)，

因此(999)。

方案1

假设求和的三个数按递增顺序为\( x, y \)和\( z \)。

若\( x = 1 \)，则\( y \)至少为2以避免重复；另一方面，\( y \)不能大于49，否则\( z \)会更小。因此\( y \)的取值范围是2–49，共48种可能。

若\( x = 2 \)，则\( y \)至少为3以避免重复。若\( y = {49} \)，则其等于\( z \)，这是不允许的。因此\( y \)的取值范围是\( 3 - {48} \)，共46种可能。

若\( x = 3 \)，则\( y \)的取值范围是4–48，共45种可能。依此类推，我们得到下表所示的小计。注意，当\( x \)为奇数时，\( y \)与\( z \)必不相等，因为一奇一偶；而当\( x \)为偶数时，我们需小心避免\( y = z \)的情况。这解释了表中向下移动时小计交替递减的模式。

\( x \)	\( y \)	小计
1	2-49	48
2	3-48	46	)-2
3	4-48	45	) -1
4	5-47	43	)-2
\( \vdots \)	\( \vdots \)	\( \vdots \)	) -1
29	30-35	6
30	31-34	4	) -2
31	32-34	3	) -1
32	33	1	) -2

因此总和的总数为

\[ 1 + 3 + 4 + 6 + 7 + 9 + \cdots + {40} + {42} + {43} + {45} + {46} + {48}, \]

或

\[ 1 + 4 + 7 + \cdots + {40} + {43} + {46} \]

\[ + {48} + {45} + {42} + \cdots + 9 + 6 + 3 \]

由于表中有32行，上述求和共有16对数，每对和为49，因此总和为\( {49} \times {16} = {784} \)，即784。

方法二

每个形如\( {100} = {61} + {34} + 5 \)的和可以看作一排三种颜色的计数器，例如61个红色计数器，接着34个绿色计数器，再接着5个蓝色计数器。

我们首先计算允许某些颜色数量相等、且相同数字不同排列(颜色)分别计数的所有计数器排列数。此时，每一种选择对应于在上图中选择两个箭头的位置。这两个箭头位置不同且不在第一个计数器上，因此共有99个可选位置。

从99个位置中选2个的方法数为\( {99} \times {98} \div 2 \)，因为先选一个计数器再选另一个共有\( {99} \times {98} \)种方式，但每对都被计算了两次。也就是说，共有\( {99} \times {49} = {4851} \)种方式排列红、绿、蓝计数器。

我们需要排除那些\( a + b + c \)中\( a, b \)和\( c \)有两个或更多相同的排列。由于\( a = b = c \)不可能，我们只需排除\( a = b \)、\( a = c \)或\( b = c \)的情况。

对于\( a = b \)，有49种可能，从\( 1 + 1 + {98} \)到\( {49} + {49} + 2 \)。同样，\( a = c \)和\( b = c \)也各有49种可能。因此共有\( {99} \times {49} - 3 \times {49} = {96} \times {49} \)种排列满足\( a, b \)和\( c \)互不相同。

然而，每个\( {100} = a + b + c \)且\( a, b \)与\( c \)不同的和在此被计数了6次，对应于\( a + b + c, a + c + b, b + a + c, b + c + a, c + a + b \)和\( c + b + a \)。因此，将100写成三个正整数之和且顺序无关的方法数为\( {96} \times {49} \div 6 = {16} \times {49} = {784} \)，

即784。

第四个数不能选4，因为存在边长为2、3、4的三角形，由于\( 2 + 3 > 4 \)。因此我们选5。这可行，因为若\( a \)和\( b \)选自\( \{ 1,2,3\} \)，则\( a + b \leq 5 \)，所以\( a, b,5 \)无法构成三角形。

同样的原则告诉我们第五个选择是\( 8 - 3,5,6 \)，且3、5、7都能构成三角形，但8无法与\( \{ 1,2,3,5\} \)中的两个数构成三角形，因为8等于两个最大数之和。

一般而言，此后每次选择都是前两个选择之和，从而得到斐波那契数列。

\[ 1,2,3,5,8,{13},{21},{34},{55},{89},{144},{233},{377},{610},{987},{1597},\ldots \]

前15个这样的数(到987为止)给出了一个不含三角形的15元集合，似乎不可能超过15个。

为了说明最多只能有15个元素，假设我们按顺序排列所选数字:\( 1 \leq a < b < c < d < e < \cdots \)。那么\( a \geq 1, b \geq 2 \)，且\( c \geq 3 \)。

由于\( b, c \)和\( d \)无法构成三角形\( d \geq b + c \geq 2 + 3 = 5 \)。类似地\( e \geq c + d \geq 3 + 5 = 8 \)，依此类推:每个数都大于或等于对应的斐波那契数(Fibonacci number)。

因此列表中不可能有第16个元素——它必须是\( p \geq {1597} \)。因此，最多可选的元素数量为15，

故为(15)。

对于网格中每列的3条水平线，路径必须占据其中1条或3条线。用这些线生成一个7位代码。例如，我们可以横向读取题目中的图示得到代码3313111。

考虑初始的连续'3'块(可能没有'3')后接一个1。此时路径必须形成如下之一的'S'形:

接着路径向右移动一列，对于下一个'3'块，它会形成上述的'Z'形但上下颠倒。如此继续贯穿整个网格，每次路径都由代码唯一确定。

共有\( {2}^{7} = {128} \)种可能的7位'1'和'3'代码，但并非全部有效。为确保路径终点在Bryn(而非右下角)，代码中'1'的数量必须为偶数。然而这恰好是所有128种代码的一半，因为对于每个含偶数个'1'的代码，都存在唯一对应的含奇数个'1'的代码(通过交换'1'和'3'得到)。因此可能的路径数量为\( {128} \div 2 = {64} \)，故为(64)。

解法二

对于一个3行\( n \)列的网格，设\( {A}_{n} \)为从左下角到右上角的路径数，\( {B}_{n} \)为从左下角到右下角的路径数。我们需要求\( {A}_{8} \)。

通过观察，可列出前几个数值:

\( n \)	1	2	3	4	5	6	7	8
\( {A}_{n} \)	1	1	2
\( {B}_{n} \)	0	1	2

对于\( n > 3 \)，每条路径要么从右上角垂直进入，要么水平进入。设\( k \geq 0 \)为路径最后一段水平线段的数量。为了确保右下角被访问，\( k + 1 \)最右列只有一种可能，如图所示。

然后对于\( k = 1,\ldots , n - 1 \)，每种情况下的路径数等于到达标记为*的点的路径数，即\( {B}_{n - k - 1} \)。此外，还有\( k = n - 1 \)的情况，此时只有一种可能。因此\( {A}_{n} = {B}_{n - 1} + {B}_{n - 2} + \cdots + {B}_{1} + 1 \)。例如\( {A}_{4} = {B}_{3} + {B}_{2} + {B}_{1} + 1 = 2 + 1 + 0 + 1 = 4 \)。

对于\( {B}_{n} \)，类似的分析得出\( {B}_{n} = {A}_{n - 1} + {A}_{n - 2} + \cdots + {A}_{1} \)，因此\( {B}_{4} = \)\( {A}_{3} + {A}_{2} + {A}_{1} = 2 + 1 + 1 = 4 \)。利用这些公式，可以完成表格:

\( n \)	1	2	3	4	5	6	7	8
\( {A}_{n} \)	1	1	2	4	8	16	32	64
\( {B}_{n} \)	0	1	2	4	8	16	32	64

因此Felix有\( {A}_{8} = {64} \)条可能的路径，故答案为(64)。

高年级解答

\( 4 - 7 = - 3 \)hence (C).

矩形的两条对角线在其两条对角线的中点相交。其中一条对角线的端点为(1,8)和(7,4)。通过取坐标平均值可找到中点\( \left( {\frac{1 + 7}{2},\frac{8 + 4}{2}}\right) = \left( {4,6}\right) \)

故答案为(A)。

设梯形(亦即阴影平行四边形)的垂直高为\( h \)，则大梯形面积为\( \frac{1}{2}\left( {3 + 5}\right) h = {4h} \)，阴影平行四边形面积为\( {1h} = h \)。因此\( \frac{1}{4} \)的面积被阴影覆盖，故答案为(C)。

解法二

在这五个矩形组成的网格中，梯形被阴影覆盖。由于最后两个矩形合起来有一半被阴影覆盖，故梯形面积为4个网格矩形。

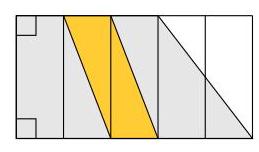
金色区域为两个半网格矩形，共1个网格矩形。因此这是梯形面积的\( \frac{1}{4} \)，

故答案为(C)。

故答案为(E)。

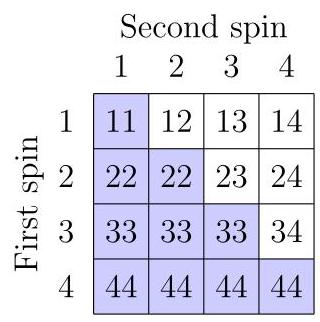
唯一得到12点的方法是大骰子掷出11点，小骰子掷出1点。由于这两次掷骰相互独立，

\[ P\left( {\text{total }{12}}\right) = P\left( {{11}\text{ on large dice }}\right) \times P\left( {1\text{ on small dice }}\right) = \frac{1}{6} \times \frac{1}{2} = \frac{1}{12} \]

故选(D)。

方法二

这些掷骰结果可视为如下\( 6 \times 6 \)的36种等可能结果表:

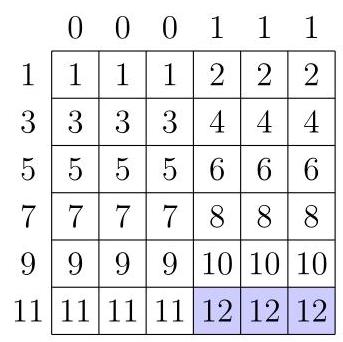
如图所示，36种结果中有3种总和为12，因此概率为\( \frac{3}{36} = \frac{1}{12} \)，

故选(D)。

因此，0.7是五个选项中最接近的，

故选(C)。

反之，所有满足\( p = q \)的数对都有\( p * q = q * p \)。

所以\( \left( {-6, - 6}\right) ,\left( {-5, - 5}\right) ,\ldots ,\left( {0,0}\right) ,\left( {1,1}\right) ,\ldots ,\left( {6,6}\right) \)是13种可能的数对，

故选(B)。

故选(C)。

因此选(D)。

因此，再次根据毕达哥拉斯定理(Pythagoras’ theorem)，\( {CD} = \sqrt{3 - \frac{3}{4}} = \frac{3}{2} \)，

因此(B)。

{3}^{x} + {3}^{x + 1} + {3}^{x + 2} = {13}\sqrt{3} \]

\[ {3}^{x}\left( {1 + 3 + {3}^{2}}\right) = {13}\sqrt{3} \]

\[ {3}^{x} = \sqrt{3} = {3}^{\frac{1}{2}} \]

\[ x = \frac{1}{2} \]

因此(B)。

\[ Y = \frac{1}{20} + 3 \times \left( {\frac{1}{22} - \frac{1}{20}}\right) = \frac{3}{22} - \frac{2}{20} = \frac{3}{22} - \frac{1}{10} = \frac{{15} - {11}}{110} = \frac{2}{55} \]

因此选(D)。

根据图中的标注，注意\( {AZ} = \frac{1}{4}{AC} \)和\( {AX} = \frac{3}{4}{AB} \)。因此，\( \bigtriangleup {AXZ} \)的面积是\( \bigtriangleup {ABC} \)面积的\( \frac{1}{4} \times \frac{3}{4} = \frac{3}{16} \)。

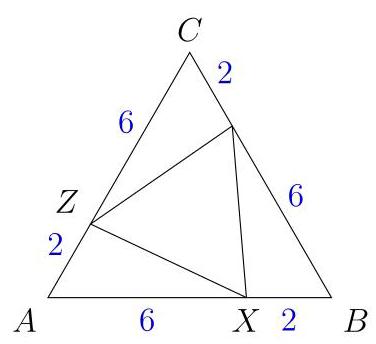
其他较小的三角形也是如此，因此它们的总面积是\( {ABC} \)的\( \frac{9}{16} \)。

从较大的等边三角形中移除这三个三角形后，形成了较小的等边三角形，剩余面积为\( \frac{7}{16} \)。因此，比值为\( 7 : {16} \)，

因此(B)。

方案2

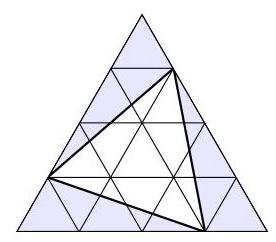
将大三角形的每条边分成4等份，并绘制一个由16个等边三角形组成的网格作为面积单位。每个阴影三角形都是一个面积为6的平行四边形的一半，因此其面积为3。

因此，未阴影三角形的面积为\( {16} - 9 = 7 \)。因此，这个三角形的面积是大三角形面积的\( \frac{7}{16} \)，

因此(B)。

同样，仅由\( P \)和\( Q \)构成的金字塔，其体积是\( P \)体积的\( {2}^{3} = 8 \)倍，即\( 8 \times 5 = {40}{\mathrm{\;{cm}}}^{3} \)。

那么块\( R \)的体积为\( {135} - {40} = {95}{\mathrm{\;{cm}}}^{3} \)，

因此选(D)。

\[ {a}_{3} = \frac{{a}_{2} + 1}{{a}_{1}} = \frac{2 + 1}{1} = 3 \]

\[ {a}_{4} = \frac{{a}_{3} + 1}{{a}_{2}} = \frac{3 + 1}{2} = 2 \]

\[ {a}_{5} = \frac{{a}_{4} + 1}{{a}_{3}} = \frac{2 + 1}{3} = 1 \]

\[ {a}_{6} = \frac{{a}_{5} + 1}{{a}_{4}} = \frac{1 + 1}{2} = 1 \]

\[ {a}_{7} = \frac{{a}_{6} + 1}{{a}_{5}} = \frac{1 + 1}{1} = 2 \]

由于每一项仅取决于前两项，\( {a}_{1} = {a}_{6} = 1 \) 和 \( {a}_{2} = {a}_{7} = 2 \) 这对组合的重复意味着模式 \( 1,2,3,2,1,1,2,3,2,1,\ldots \) 将持续下去，每五项重复一次。因此 \( {a}_{100} = {a}_{5} = 1 \)，故选 (A)。

按图示标注各点，其中\( M \)为\( {BC} \)的中点。根据毕达哥拉斯定理(Pythagoras’ theorem)，\( {PB} = {PC} = \sqrt{{8}^{2} + {1}^{2}} = \)\( \sqrt{65} \)。

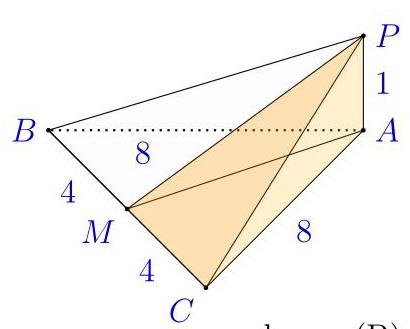
因此(B)。

由于\( \bigtriangleup {PBC} \)是等腰三角形，\( \bigtriangleup {PMC} \)在\( M \)处有一个直角，

然后\( {MP} = \sqrt{{\left( \sqrt{65}\right) }^{2} - {4}^{2}} = \sqrt{49} = 7 \)。

那么\( \bigtriangleup {PBC} \)的底为\( {BC} = 8 \)，高为\( {MP} = 7 \)，面积为\( \frac{1}{2} \times 8 \times 7 = {28} \)，

该体积为虚线立方体减去8个被截去的金字塔。立方体的边长为\( 2\sqrt{2} \)，因此其体积为\( {\left( 2\sqrt{2}\right) }^{3} = {16}\sqrt{2} \)。考虑其中一个被截去的金字塔:它有三条虚线边，每条长度为\( \sqrt{2} \)；其底面积为\( A = \frac{1}{2}\sqrt{2}\sqrt{2} = 1 \)，故其体积为\( \frac{1}{3}{Ah} = \frac{\sqrt{2}}{3} \)。由于共有8个相同的角，它们的总体积为\( \frac{8\sqrt{2}}{3} \)。

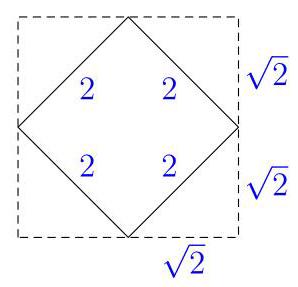
因此，截角立方八面体(cuboctahedron)的体积为\( {16}\sqrt{2} - \frac{8\sqrt{2}}{3} = \frac{{40}\sqrt{2}}{3} \)，

因此(B)。

方案2

与第一种解法相同，原立方体的正方形边长为\( 2\sqrt{2} \)，因此这些正方形的对角线长度为4。我们可以做4次垂直切割，将其切成一个\( 2 \times 2 \times 2\sqrt{2} \)棱柱和4个以矩形为底的棱锥，如图所示。

该棱柱的体积为\( 8\sqrt{2} \)。

这4个棱锥的每个底面都是面积为\( 2 \times 2\sqrt{2} = 4\sqrt{2} \)的矩形，且垂直高度为1，如俯视图所示。因此其体积为\( \frac{1}{3} \times 4\sqrt{2} = \)\( \frac{4}{3}\sqrt{2} \)。于是截角立方八面体(cuboctahedron)的体积为

\[ 8\sqrt{2} + 4 \times \frac{4}{3}\sqrt{2} = \frac{{24} + {16}}{3}\sqrt{2} = \frac{{40}\sqrt{2}}{3} \]

故选(B)。

\[ x = \frac{b + c}{a}\;\text{ and }\;y = \frac{f - e}{d} \]

因此\( x \)必须为正，但\( y \)可为负。为使\( x + y, f \)最小，应使\( e \)。当\( f = 2, e = 9 \)且\( d = 1 \)时，\( y \)取最小值，得\( y = - 7 \)。于是\( x + y \)大于-7。

于是，当\( d, e, f \)如上且\( b = 3, c = 4 \)，\( a = 8 \)时，有\( x = \frac{7}{8} < 1 \)，从而\( x + y < - 6 \)。无论这是否为\( x + y \)的最小可能值，我们已知该最小值介于-7与-5之间，故选(B)。

由于我们只关心比例，设半圆半径为1。由于下图中的虚线半径与对应切线垂直，大三角形由4个较小的直角等腰三角形组成，其边长分别为1、1和\( \sqrt{2} \)。因此大三角形面积为2。

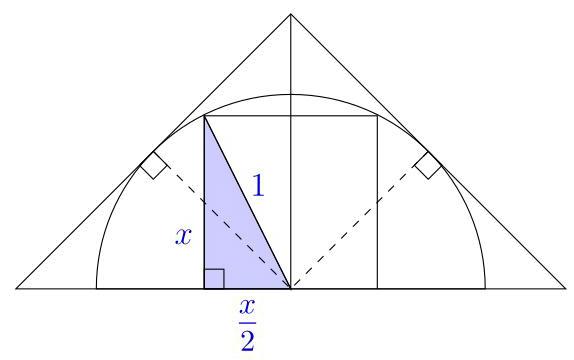
设\( x \)为正方形的边长。由连接正方形角点与圆心所形成的三角形，得\( {x}^{2} + {\left( \frac{x}{2}\right) }^{2} = 1 \)，从而\( x = \frac{2}{\sqrt{5}} \)。于是正方形面积为\( \frac{4}{5} \)，所求面积比为\( \frac{4}{5} : 2 = 2 : 5 \)，

故选(C)。

方案2

选取长度单位使正方形边长为2，从而面积为4。由对称性，半圆圆心位于正方形下侧边的中点。根据勾股定理，半圆半径为\( \sqrt{5} \)。将图形沿半圆直径作镜像，得到一个半径为\( \sqrt{5} \)的圆内接于正方形。该正方形边长为\( 2\sqrt{5} \)，面积为\( {\left( 2\sqrt{5}\right) }^{2} = {20} \)。于是原三角形面积为10，面积比为\( 4 : {10} = 2 : 5 \)，故选(C)。

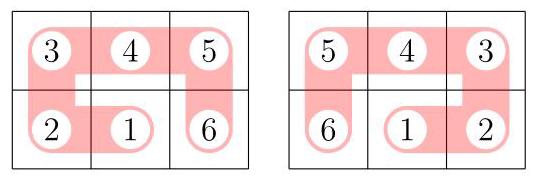
四个角均如此，共得16种放置方式。

若从中心格开始，则有三种可能:

四个中心格皆如此，共得12种摆法。总计有\( {16} + {12} = {28} \)种摆法，故选(D)。

\[ {77}\left( {\frac{4}{3} - \frac{6}{5}}\right) = \frac{154}{15} \approx {10}\text{ minutes } \]

故选(E)。

正六边形由六个面积为10的等边三角形组成，可作为测量网格。

图示为Horton测量的三种不同(不全等)三角形。借助网格，可测得每种三角形的面积；再考虑旋转与反射，可统计各类数量:故得(360)。

于是这20个三角形的总面积为

\[ {12} \times {20} + 6 \times {10} + 2 \times {30} = {240} + {60} + {60} = {360}, \]

已知\( s \)为偶数，故\( f \)为偶四次方；为使其最小，必形如\( f = {2}^{4} \times {3}^{4k} \)，其中\( k \geq 1 \)。

因\( c \)为奇立方且为\( f \)的因数，必形如\( c = {3}^{3\ell } \)，于是\( s = {2}^{4} \times {3}^{{4k} - 3\ell } \)。但\( s \)为平方，故指数\( {4k} - 3\ell \)须为非负偶数。

最小解为\( k = \ell = 2 \)，于是\( s = {2}^{4} \times {3}^{2} = {144}, c = {3}^{6} = {729} \)，且\( s + c = {144} + {729} = {873}, \)

故得(873)。

若各项为\( {a}_{1},{a}_{2},\ldots \)，则\( {a}_{n} = \frac{1}{2}\left( {{a}_{n - 1} + {a}_{n + 1}}\right) - 1 \)，于是\( {a}_{n - 1} + 2{a}_{n} + {a}_{n + 1} = 2 \)。可将此方程改写为\( {a}_{n} - {a}_{n - 1} + 2 = {a}_{n + 1} - {a}_{n} \)，故相邻两项之差每次增加2。因此，

\[ {a}_{n} - {a}_{n - 1} = 2 + {a}_{n - 1} - {a}_{n - 2} \]

\[ = 4 + {a}_{n - 1} - {a}_{n - 2} \]

\[ = \cdots \]

\[ = 2\left( {n - 2}\right) + {a}_{2} - {a}_{1} = {2n} \]

于是

\[ {a}_{n} = {a}_{1} + \left( {{a}_{2} - {a}_{1}}\right) + \left( {{a}_{3} - {a}_{2}}\right) + \cdots + \left( {{a}_{n - 1} - {a}_{n - 2}}\right) + \left( {{a}_{n} - {a}_{n - 1}}\right) \]

\[ = 2 + 4 + 6 + \cdots + {2n} \]

\[ = n\left( {n + 1}\right) \]

为了找出小于1000的最大值\( {a}_{n} = n\left( {n + 1}\right) \)，我们注意到\( {a}_{30} = {30} \times {31} = {930} \)，于是\( {a}_{31} = {a}_{30} + 2 \times {31} = {992} \)且\( {a}_{32} = {a}_{31} + 2 \times {32} = {1056} \)。因此992是小于1000的最大项，

方法二

若连续三项为\( a, b, c \)，则\( b = \frac{a + c}{2} - 1 \)，使得\( c = {2b} - a + 2 \)。利用此规则，序列继续:

\[ 2,6,{12},{20},{30},{42},\ldots \]

由此我们断言第\( n \)项为\( n\left( {n + 1}\right) \)。

假设此断言成立，我们需要小于1000的最大\( n\left( {n + 1}\right) \)值。由于\( n\left( {n + 1}\right) = \)\( {n}^{2} + n \approx {n}^{2} \)，我们检查\( n \approx \sqrt{1000} \approx {31.6} \)。于是\( {31} \times {32} = {992} \)且\( {32} \times {33} = {1056} \)，因此小于1000的最大项为992。

我们用对\( n \)的强归纳法来证明该断言。待证命题为:对于\( n \geq 1 \)，第\( n \)项由公式\( n\left( {n + 1}\right) \)给出。这对\( n = 1,2 \)成立。对于\( n \geq 3 \)，设项\( n - 2, n - 1 \)与\( n \)为\( a, b, c \)如上，则根据归纳假设，\( a = \left( {n - 2}\right) \left( {n - 1}\right) \)且\( b = \left( {n - 1}\right) n \)。于是

\[ c = {2b} - a + 2 = {2n}\left( {n - 1}\right) - \left( {n - 2}\right) \left( {n - 1}\right) + 2 = {n}^{2} + n = n\left( {n + 1}\right) \]

因此第\( n \)项为\( n\left( {n + 1}\right) \)，归纳完成。

通过强归纳法，该断言得证，且992是小于1000的最大项，故答案为(992)。

在初始阶段0，Wayne拥有未盖章的原件。因此有1张纸，其“COPY”印章出现次数为0。

阶段1后，他有未盖章的原件以及两份已盖章的复印件。因此有1张纸印章数为0，2张纸印章数为1。

阶段2后，他有未盖章的原件、最初的两份复印件，以及这些复印件各自的两份已盖章复印件。因此有1张纸印章数为0，4张纸印章数为1，4张纸印章数为2。

我们建立一张表来追踪具有特定印章数的纸张数量。在每一阶段，印章数为\( k \)的纸张数量等于上一阶段印章数为\( k \)的纸张数量(这些纸张被送入复印机但未再次盖章)加上上一阶段印章数为\( k - 1 \)的纸张数量的两倍(每份生成两份新复印件，各多盖一个章)。此外，始终只有一份未盖章的原件。由于我们只关心印章数为2的复印件数量，表格的关键部分如下:

阶段	邮票数量
	0	1	2
0	1	0	0
1	1	2	0
2	1	4	4
3	1	6	12
4	1	8	24
5	1	10	40
6	1	12	60
7	1	14	84
8	1	16	112

因此，经过8个阶段后，共有112张纸，每张纸上有2张邮票，

因此(112)。

方案2

除了盖章之外，假设韦恩在每一步都会写一个数字0、1或2，分别表示该页是原件、第一复印件或第二复印件。他会从左到右在每一页上写下这些数字。

最终的\( {3}^{8} \)页纸叠将包含从\( {00000000} = 0 \)到\( {22222222} = {3}^{8} - 1 \)的所有8位三进制数。盖有两枚印章的页码是那些恰好有两个非零数字的数。选择这两个非零数字位置的方法共有\( \left( \begin{array}{l} 8 \\ 2 \end{array}\right) = {28} \)种。对于每一种位置选择，每个非零数字可以是1或2，因此有4种可能。总共有\( {28} \times 4 = {112} \)种可能。

因此(112)。

方案3

在复制过程的第\( n \)阶段之后，共有\( {3}^{n} \)张纸，每张纸上的邮票数量介于0到\( n \)之间。每个邮票数量的页数可由前一阶段轻松推算。例如，若在第\( n \)阶段后有\( a \)页含\( k \)枚邮票，\( b \)页含\( k + 1 \)枚邮票，则到第\( n + 1 \)阶段后将有\( {2a} + b \)页含\( k + 1 \)枚邮票。因此我们可以列表如下:

阶段	0	1	2	3	...	多项式
0	1					\( {\left( 1 + 2x\right) }^{0} = 1 \)
1	1	2				\( {\left( 1 + 2x\right) }^{1} = 1 + {2x} \)
2	1	4	4			\( {\left( 1 + 2x\right) }^{2} = 1 + {4x} + 4{x}^{2} \)
3	1	6	12	8		\( {\left( 1 + 2x\right) }^{3} = 1 + {6x} + {12}{x}^{2} + 8{x}^{3} \)
\( \vdots \)	\( \vdots \)					\( \vdots \)

这一迭代过程与表中最后一列所示\( {\left( 1 + 2x\right) }^{n} \)中\( {x}^{k} \)的系数计算方式相同。当乘以\( \left( {1 + {2x}}\right) \)时，\( {\left( 1 + 2x\right) }^{n + 1} \)中\( {x}^{k + 1} \)的系数等于\( {x}^{k} \)的系数的两倍再加上\( {\left( 1 + 2x\right) }^{n} \)中\( {x}^{k + 1} \)的系数。

\( {\left( 1 + 2x\right) }^{8} \)中的\( {x}^{2} \)项为\( \left( \begin{array}{l} 8 \\ 2 \end{array}\right) {1}^{6}{\left( 2x\right) }^{2} = {112}{x}^{2} \)，其系数为112，这也是拥有2枚邮票的页数，

因此为(112)。

我们首先计算五位选手完成比赛的所有可能方式，且每人本周的名次与上周不同。这等于\( A, B, C, D, E \)的错位排列数。当用循环记号表示时，它必须是一个5-循环，如(A, C, E, B, D)，或一个3-循环加一个2-循环，如\( \left( {A, E, D}\right) \left( {B, C}\right) \)。共有\( 4! = {245} \)个5-循环和\( \left( \begin{array}{l} 5 \\ 3 \end{array}\right) \times 2 = {20} \)个由3-循环与2-循环组成的排列。因此，共有\( {24} + {20} = {44} \)种方式使五位选手的名次与上周不同。

在这44种排列的每一种中，都会出现一些“上升”选手(第二场比赛名次高于第一场)和一些“下降”选手(相反)。

只有1种情况有4位上升选手和1位下降选手，顺序为BCDEA，对应5-循环(A, E, D, C, B)。其逆排列则给出唯一1种4位下降选手和1位上升选手的情况，顺序为\( {EABCD} \)，对应5-循环(A, B, C, D, E)。其余42种排列中，一半为3升2降，另一半为3降2升。这是因为逆排列实际上交换了第一、二场比赛，并将名次上升变为下降，反之亦然，从而在这两组排列之间建立一一对应。

因此共有21种可能，

故为(21)。方法2

将选手标记为\( \mathrm{A} \)到\( \mathrm{E} \)，我们用\( \mathrm{C} \uparrow \)表示\( \mathrm{C} \)在第二场比赛的名次高于第一场。于是\( \mathrm{E} \uparrow \)且\( \mathrm{A} \downarrow \)。

另一位选手将上升，产生3种情况:\( \mathrm{B} \uparrow ,\mathrm{C} \uparrow \)或\( \mathrm{D} \uparrow \)。

第一种情况:\( \mathrm{B} \uparrow ,\mathrm{E} \uparrow ,\mathrm{A} \downarrow ,\mathrm{C} \downarrow \)且\( \mathrm{D} \downarrow \)。第二场比赛的可能结果见表1:B必须升至第1，D必须降至第5，C降至第4，A和E可互换，共2种可能。

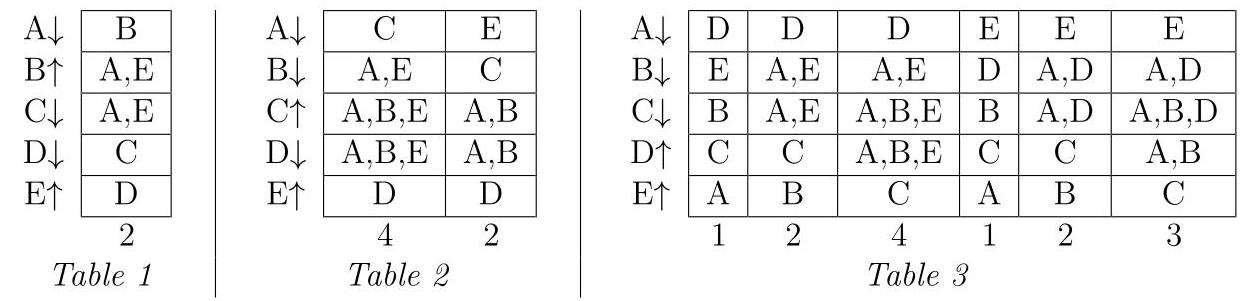
表2总结了当\( \mathrm{C} \uparrow ,\mathrm{E} \uparrow ,\mathrm{A} \downarrow ,\mathrm{B} \downarrow \)和\( \mathrm{D} \downarrow \)时的可能性。D必须降至第5位，只有\( \mathrm{C} \)或\( \mathrm{E} \)能最终成为第1位，因此我们分别考虑这两种情况。如果\( \mathrm{C} \)是第1位，那么第2位必须是A或E。同时B必须是第3位或第4位。这给出了4种可能性。如果E是第1位，那么C必须是第2位。这样第3位和第4位留给A和B，如表所示。因此表2共包含6种可能性。

表3总结了当\( \mathrm{D} \uparrow ,\mathrm{E} \uparrow ,\mathrm{A} \downarrow ,\mathrm{B} \downarrow \)和\( \mathrm{C} \downarrow \)时的可能性。6列分别考虑基于第1位和第5位的6种子情况。注意\( \mathrm{C} \)必须最终排在第4位或第5位，因此在A或B排在第5位的子情况中，C必须排在第4位，这使得可能性极少。将这6种子情况相加，共得到\( 1 + 2 + 4 + 1 + 2 + 3 = {13} \)种可能性。总体而言，我们已统计了\( 2 + 6 + {13} = {21} \)种可能性，因此得到(21)。

答案

问题	小学中段	小学高段	初中	中级	高级
1	C	E	E	C	C
2	D	D	C	A	B
3	B	C	B	B	E
4	B	B	D	A	E
5	A	C	D	B	A
6	D	A	B	C	C
7	E	E	E	C	E
8	B	C	D	E	A
9	C	E	B	A	D
10	A	A	A	D	C
11	B	D	C	A	B
12	E	E	C	C	C
13	B	D	E	D	D
14	A	A	C	E	B
15	B	D	D	D	B
16	B	C	C	C	D
17	E	D	A	D	B
18	E	A	B	C	D
19	D	B	D	D	A
20	C	C	D	C	B
21	C	B	C	B	B
22	E	E	C	B	B
23	C	B	C	B	C
24	C	A	C	D	D
25	D	E	A	E	E
26	258	56	497	475	360
27	138	405	27	999	873
28	990	151	47	784	992
29	56	150	360	15	112
30	151	189	784	64	21