澳大利亚AMC-10年级D

2022

AUSTRALIAN MATHEMATICS COMPETITION

Instructions and Information [ 0 0 0

General O O O O

There are 25 multiple-choice questions, each requiring a single answer, and 5 questions that require a whole number answer between 000 and 999 . The questions generally get harder as you work through theasdanseedamc paper. There is no penalty for an incorrect response.

O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O

NO calculators, maths stencils, mobile phones or other calculating aids are permitted. Scribbling paper, graph paper, ruler and compasses are permitted, but are not essential.

考生禁止携带计算器、数学模板尺、手机或其他计算工具, 允许使用草稿纸、坐标纸、直尺和圆规。

Diagrams are NOT drawn to scale. They are intended only as aids. 图形只作为辅助参考,并未按照实际比例绘制。

This is a competition not a test; do not expect to answer all questions. You are only competing against your own grade in your own country/Australian state so different grades doing the same paper are not compared.

这是一场比赛,而不是一场测验,你无需在规定时间内做完全部题目。你只会与你所在年级的参赛者进行评比,所以即使做同一份试卷,所在年级不同也不会一同评比。

Read the instructions on the answer sheet carefully. Ensure your name, school name, level, school grade and exam code are entered. It is your responsibility to correctly code your answer sheet.

务必仔细O O 答题卡上的O O O O 。确保O O O O O O 姓名、在读学校、考试等级、考试年级和准考证号。

When your teacher gives the signal, begin working on the problems 监考老师发出作答指令后,方可开始答题。

Integrity of the competition

The AMT reserves the right to re-examine students before deciding whether to grant official status to their score.

Reminder

You may sit this competition once, in one division only, or risk no score.

AUSTRALIAN

MATHS TRUST

Intermediate

Grades 10-11

TIME ALLOWED

75 minutes

The answer sheet 答题卡说明

Mark your exam code and answers with a \( {2B} \) pencil.

使用 2B 铅笔正确填涂准考证号和答案。

Record your answers on the answer sheet provided (not on the question paper) by FULLY colouring the circle matching your answer.

将答案全部涂在答题卡上(在试卷上作答无效)。

Your answer sheet will be scanned. The optical scanner will attempt to read all markings even if they are in the wrong places, so please be careful not to doodle or write anything extra on the answer sheet. If you want to change an answer or remove any marks, use a plastic eraser and be sure to remove all marks and smudges.

你的答题卡将通过扫卡机进行扫描,读卡机会读出答题卡上的所有标记,所以不要在答题卡上乱写乱画。修改答案时务必用橡皮擦干净,保持答题卡清洁。

Intermediate Division

1-10 题, 每题 3 分

Questions 1 to10,3marks each

算式 \( {2220} - {2022} = \)

\( {2220} - {2022} = \)

(A) 18 (B) 188 (C) 198 (D) 200 (E) 202

右侧图案是由 29 个 \( 1\mathrm{\;{cm}} \times 1\mathrm{\;{cm}} \) 的小正方形组成的。请问这个图案的周长是多少 \( \mathrm{{cm}} \) ？ This shape is built from 29 squares, each \( 1\mathrm{\;{cm}} \times 1\mathrm{\;{cm}} \) . What is its perimeter in centimetres?

(A) 52 (B) 58 (C) 60

(D) 68 (E) 72

右侧电子时钟显示的时间为 20:22。 2022 请问到凌晨 00:00 还要多少分钟?

A digital clock shows the time as 20:22.

In how many minutes will it be midnight?

(A) 158 (B) 218 (C) 258 (D) 278 (E) 378

算式 \( \frac{{1}^{2} + {2}^{2}}{{3}^{2} + {4}^{2}} \) 的值等于多少?

The value of \( \frac{{1}^{2} + {2}^{2}}{{3}^{2} + {4}^{2}} \) is

(A) \( \frac{1}{5} \) (B) \( \frac{3}{7} \) (C) \( \frac{9}{49} \) (D) 4 (E) 5

右图所示的三角形 \( {PQR} \) 中, \( {PQ} = {PR} \) 且

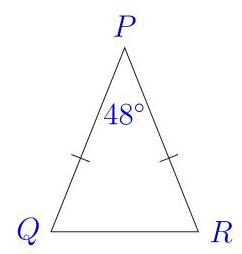
\( \angle {QPR} = {48}^{ \circ } \) 。

请问 \( \angle {PQR} \) 的度数是多少?

In the triangle \( {PQR} \) shown, \( {PQ} = {PR} \) and \( \angle {QPR} = {48}^{ \circ } \) . What is \( \angle {PQR} \) ?

(A) \( {60}^{ \circ } \) (B) 66° (C) \( {72}^{ \circ } \) (D) 78° (E) \( {84}^{ \circ } \)

请问右图矩形的几分之几被涂上 0 阴影?

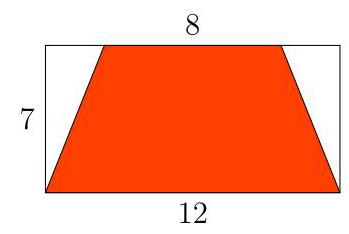
What fraction of this rectangle is shaded?

(A) \( \frac{1}{2} \) (B) \( \frac{5}{8} \) (C) \( \frac{5}{6} \) (D) \( \frac{2}{3} \) (E) \( \frac{7}{12} \)

算式 \( {\left( {0.4}\right) }^{2} + {\left( {0.1}\right) }^{2} = \)

\( {\left( {0.4}\right) }^{2} + {\left( {0.1}\right) }^{2} = \)

(A) 0.25 (B) 1.7 (C) 0.17 (D) 1 (E) 0.26

□□□□每天使用 16000 □升汽油。

现有储备的汽油足够使用 60 天。

请问 0 0 0 还需要购买多少汽油才能有足够 90 天的储备 0 ？

(A) 4 百万升 (B) 4.8 百万升 (C) 480 0 0 升

(D) 160 0 0 升 (E) 4800 I I I

Australia uses 160 million litres of petrol each day.

There is enough petrol stored to last 60 days.

How much more petrol does Australia need to buy to have enough stored for 90 days?

(A) 4 million litres (B) 4.8 million litres (C) 480 million litres

(D) 160 million litres (E) 4800 million litres

算式 \( \frac{2022}{2} - \frac{2022}{3} = \)

\( \frac{2022}{2} - \frac{2022}{3} = \)

10.

请问方程中的 \( \bigtriangleup \) 是下列哪个代数式?

\[ \bigtriangleup + \bigtriangleup + \bigtriangleup = {27}{x}^{3}{y}^{6} \]

Which algebraic term should replace \( \bigtriangleup \) in the equation below?

\[ \bigtriangleup + \bigtriangleup + \bigtriangleup = {27}{x}^{3}{y}^{6} \]

(A) \( {3x}{y}^{2} \) (B) \( 3{x}^{3}{y}^{6} \) (C) \( {9x}{y}^{2} \) (D) \( 9{x}^{3}{y}^{6} \) (E) \( {27x}{y}^{2} \)

11-20 题, 每题 4 分 Questions 11 to 20, 4 marks each

11.

一个矩形的三个顶点坐标为(1,4)、(7,4)与(1,8)。请问这个矩形两条对角线交点的坐标是什么？

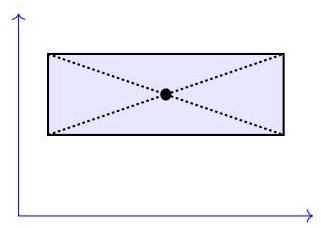
(D)(5,6) (E)(7,8)

Three vertices of a rectangle are the points(1,4), (7,4)and(1,8). At which point do the diagonals of the rectangle cross?

(A)(4,6) (B)(3,2) (C)(3,1) 12. 请问在方格内填入哪个数才能使得此等式成立？ What value should be placed in the box to satisfy the equation? (A) 1 (B) \( 1\frac{1}{2} \) (C) 2 (D) \( 2\frac{1}{2} \) (E) 3

13.

一个三角形的三个内角度数之比为 \( 2 : 3 : 4 \) 。请问其中最大角的度数是多少?

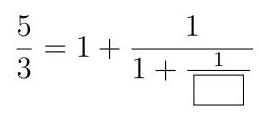
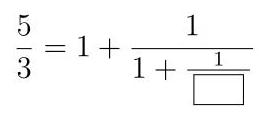
The angles of a triangle are in the ratio \( 2 : 3 : 4 \) . What is the size of the largest angle in degrees?

(A) 40 (B) 45 (C) 72 (D) 80 (E) 90

14.

O O O O O O O 游戏, 每个圆圈内都包含一个整O O O O O O O O O O O O 条O 线上 O 四个圆圈内的O 0 之和都必须等于 40。完成0 0 游戏后,请问用0 0 最大00 是 0 0 ？

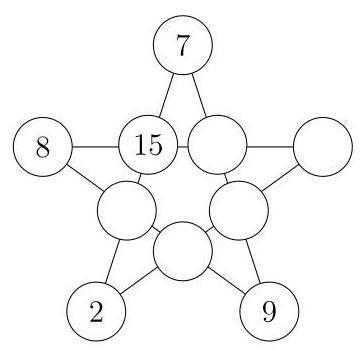
In this puzzle, each circle should contain an integer. Each of the five lines of four circles should add to 40 . When the puzzle is completed, what is the largest number used?

(A) 15 (B) 16 (C) 17 (D) 18 (E) 19

15.

小丹与小吕相约在一家咖啡厅见面。小吕 \( 0.0.以6\mathrm{\;{km}}/\mathrm{h}.0 \) 速度0.0.0.5分钟后,小丹000000骑车速度 \( {00}\mathrm{\;{km}}/\mathrm{h}{0000}\;{15} \) 分钟,他们两人同时抵达这家咖啡厅。

请问他们两人的路程总 0 是 0 0 ？

Daniel and Luke arrange to meet at a cafe. Luke leaves work, walking at \( 6\mathrm{\;{km}}/\mathrm{h} \) . Five minutes later, Daniel starts cycling from his flat at \( {20}\mathrm{\;{km}}/\mathrm{h} \) . A further 15 minutes later, both arrive at the cafe at the same time.

What is the total distance they travelled?

(A) \( {5.5}\mathrm{\;{km}} \) (B) \( 6\mathrm{\;{km}} \) (C) \( {6.5}\mathrm{\;{km}} \) (D) \( 7\mathrm{\;{km}} \) (E) \( {7.5}\mathrm{\;{km}} \)

16.

我家共有 7 位 0 0 0 5 位 0 0 0 每年我们都会聚在一起庆祝中秋节, 每位 0 0 O O 给O O O O O O O O O 一份礼物O 每位O O O 都O O O O O O O O O O O 份礼物。请问 0 0 其 0 出多少份礼物?

My family of 7 adults and 5 children gather each year to celebrate Chinese MidAutumn festival. Each adult gives one gift to everyone else. Each child gives one gift to every other child. How many gifts are given?

(A) 78 (B) 85 (C) 97 (D) 102 (E) 109

17.

使用右图转盘转动两次,依照以下规则组成一个两位数:

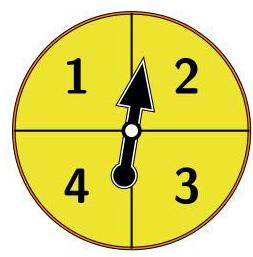
- 第一次转出的值组成这个数的十位数;

- 如果第二次转出的值大于第一次转出的值, 则组成这个两位数的个位数;

- 如果第二次转出的值不大于第一次转出的值, 则把十位上的数字重复作为个位数。

请问组成的两位数可以被 11 整除的概率是多少?

This spinner is spun twice to form a two-digit number using the following rules:

- The first value spun forms the tens digit of a number.

- If the second value rolled is larger than the first, it becomes the units digit of a number.

- If the second value spun is not larger than the first, the tens digit is repeated as the units digit.

What is the probability that the resulting two-digit number is divisible by 11?

(A) \( \frac{1}{4} \) (B) \( \frac{3}{8} \) (C) \( \frac{1}{2} \) (D) \( \frac{5}{8} \) (E) \( \frac{9}{16} \)

18.

利用八个重叠的单位正方形画出一朵花的形状,如右图所示。任意两个正方形重叠的部分都是等腰三角形。

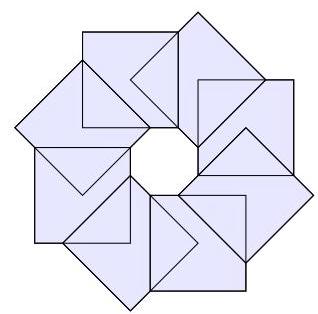
请问阴影部分的面积是多少?

Eight overlapping unit squares are drawn to produce a flower shape as shown. The parts where two squares overlap are isosceles triangles. What is the total shaded area?

(A) 5 (B) \( 5\frac{1}{2} \) (C) 6 (D) \( 6\frac{1}{2} \) (E) 7

19.

小雷与小尼最近开始学吉他。

两星期前, 小雷已经学习的天数是小尼的五倍。

两天前, 小雷已经学习的天数是小尼的两倍。

今天, 请问小雷至今已经学习的天数加上小尼至今已经学习的天数之和是多少天?

(A) 25 (B) 37 (C) 46 (D) 52 (E) 68

Rick and Nic started learning guitar recently.

Two weeks ago, Rick had been learning five times as long as Nic.

Two days ago, Rick had been learning twice as long as Nic.

Today, what is the number of days that Rick has been learning plus the number of days that Nic has been learning?

(A) 25 (B) 37 (C) 46 (D) 52 (E) 68

20.

在过去 20 年里,电视机屏幕的标准比例从 \( 4 : 3 \) 变为 \( {16} : 9 \) 。当图像比例与正在看的屏幕比例不匹配时, 通常用黑色条框来填补, 如下图所示。

\( 4 : 3 \) 的图像呈现在 \( {16} : 9 \) 的屏幕上

\( 4 : 3 \) image on a \( {16} : 9 \) screen

\( {16} : 9 \) 的图像呈现在 \( 4 : 3 \) 的屏幕上

16: 9 image on a 4:3 screen

如果 \( \ell \) 表示左图中黑色部分在图中占的比例, \( r \) 表示右图中黑色部分在图中占的比例,请问 \( \ell : r \) 等于多少?

Over the last 20 years, the standard ratio of television screens has changed from 4 : 3 to 16: 9. When the ratio of content doesn't match the ratio of the screen it is being viewed on, black bars are often used to compensate, as illustrated.

If \( \ell \) is the fraction of the screen blacked out in the left diagram, and \( r \) is the fraction of the screen blacked out in the right diagram, then the ratio \( \ell : r \) equals

(A) \( 3 : 4 \) (B) \( 8 : 9 \) (C) \( 1 : 1 \) (D) \( 9 : 8 \) (E) \( 4 : 3 \)

21-25 题,每题 5 分

Questions 21 to 25, 5 marks each

21.

一个三角形坡道是一个直角四面体。它的水平底面是一个边长为 \( 8\mathrm{\;m} \) 的正三角形。顶点位于底面一个角的正上方 \( 1\mathrm{\;m} \) 处,旁边的两个面为直角三角形。请问斜面的面积是多少 \( {\mathrm{m}}^{2} \) ？

A triangular ramp is in the shape of a right-angled tetrahedron.

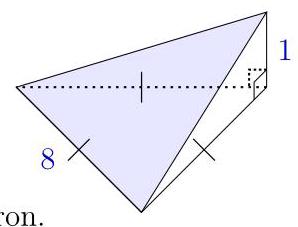
The horizontal base is an equilateral triangle with sides 8 metres. The apex is 1 metre directly above one corner of the base, so that two faces are vertical. In square metres, what is the area of the sloping face?

(A) \( {16}\sqrt{3} \) (B) 28 (C) \( \frac{65}{4}\sqrt{3} \) (D) \( 4\sqrt{33} \) (E) 32

22.

当 \( n = {2022} \) 时,请问下列表达式的值是多少?

\[ \sqrt[3]{\frac{\left( {1 \times 2 \times 4}\right) + \left( {2 \times 4 \times 8}\right) + \cdots + \left( {n \times {2n} \times {4n}}\right) }{\left( {1 \times 3 \times 9}\right) + \left( {2 \times 6 \times {18}}\right) + \cdots + \left( {n \times {3n} \times {9n}}\right) }} \]

What is the value of the following expression when \( n = {2022} \) ?

(A) \( \frac{1}{2} \) (B) \( \frac{2}{3} \) (C) \( \frac{3}{4} \) (D) \( \frac{4}{5} \) (E) \( \frac{5}{6} \)

23.

小莉将水与牛奶以 5:7 的比例混合在一个桶内,但她不小心洒出 \( 9\mathrm{\;L} \) 的混合液。于是她在桶内加入 \( 9\mathrm{\;L} \) 的水,此时水与牛奶的比例变成 \( 9 : 7 \) 。

请问原先桶内有多少 \( \mathrm{L} \) 的牛奶?

Lisa has a mixture of water and milk in a drum in the ratio 5 : 7. She accidentally spills \( 9\mathrm{\;L} \) of this mixture.

She then fills the drum with \( 9\mathrm{\;L} \) of water. This makes the water to milk ratio \( 9 : 7 \) . How many litres of milk were in the drum originally?

(A) 20 (B) 21 (C) 24 (D) 36 (E) 40

24.

□ □ \( p \) 与 \( q \) 的最大公 O O 是 \( t \) ,且 \( q = {rt} \) O O O \( p \) 与 \( q \) 的最小公倍数 \( \mathrm{O} \) O O O O Given that the highest common factor of \( p \) and \( q \) is \( t \) , and \( q = {rt} \) , then the lowest common multiple of \( p \) and \( q \) will always be equal to

(A) \( {pq} \) (B) \( {qr} \) (C) \( {rt} \) (D) \( {pr} \) (E) \( {pt} \)

25.

\( {003} \times 3 \) 方格表的每个小方格内都填0一个正数,0每一行 0 每一列上的 0 )之积都等于 1 ,每个 \( 2 \times 2 \) 的 0 正方形 0 的 O O O 积都等于 2 。请问 O O 正中央的小方格内所填的数是 0 0 ?

A positive number is written in each cell of the \( 3 \times 3 \) table. In each row and in each column, the product of the numbers is equal to 1 . In each \( 2 \times 2 \) square, the product of the numbers is equal to 2 . What is the number in the central cell?

(A) 1 (B) 2 (C) 6 (D) 8 (E) 16 问题 26-30 的答案为 000-999 之间的整数, 请将答案填在答案卡上对应的位置。第 26 题占 6 分, 第 27 题占 7 分, 第 28 题占 8 分, 第 29 题占 9 分,第 30 题占 10 分。 For questions 26 to 30, the answer is an integer from 000 to 999 . Questions 26-30 are worth 6, 7, 8, 9 and 10 marks, respectively. 26. ( 0 0 0 0 0 0 中, \( a \) 、 \( b \) ) \( c \) ) 0 非零0)。请问这个 0 0 第二行的三位数 \( {abc} \) 是 0 0 ？ In the sum shown, \( a, b \) and \( c \) are nonzero digits. What is the three-digit number \( {abc} \) in the second line of the sum? 27. 将 0 0 数相乘后,请问所得 0 0 的 0 0 0 0 0 0 0 和是 0 0 ？ When these numbers are multiplied, what is the sum of all digits in the answer?

28.

请问一共有多少种不同的方式可以将 100 写成三个不同的正整数之和? 注意:我们不考虑各项的相加顺序,所以 \( {34} + 5 + {61} \) 和 \( {61} + {34} + 5 \) 视作同一种方式。

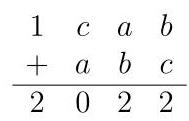
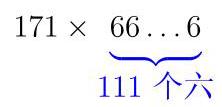
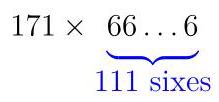
In how many ways can 100 be written as the sum of three different positive integers? Note that we do not consider sums formed by reordering the terms to be different, so that \( {34} + 5 + {61} \) and \( {61} + {34} + 5 \) are treated as the same sum.

29.

请问从集合 \( \{ 1,2,3,4,\ldots ,{1000}\} \) 中最多可以选多少个元素使得它们之中的任意三个数都不能构成一个三角形的三条边长？例如,选出的元素可以包括 20、22 和 42, 因为不存在三角形以 20、22 和 42 为边长。

What is the largest number of distinct elements that you can choose from the set \( \{ 1,2,3,4,\ldots ,{1000}\} \) such that no three of them are the side lengths of a triangle? For example the selection could include 20, 22 and 42 , since there is no triangle with sides 20, 22 and 42 .

30.

教室共有三排,每排八个座位,每个座位上都坐有学生。现在要将班级宠物菲菲从坐在角落上的小艾开始传递到对角上的小柏手中, 它必须经过每个学生且只能经过一次, 每位学生只能将它向左侧、右侧、前方或后方紧邻的位置传递。其中一条可能的传递路径如右图所示。

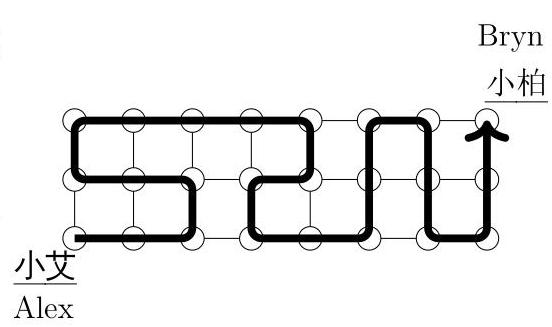
请问要将菲菲从小艾传递到小柏手中总共有多少条不同的路径？

Students sit at their desks in three rows of eight. Felix, the class pet, must be passed to each student exactly once, starting with Alex in one corner and finishing with Bryn in the opposite corner. Each student can pass only to the immediate neighbour left, right, in front or behind. One possible path is shown. How many different paths can Felix take from Alex to Bryn?