澳大利亚AMC-10年级D

2023

AUSTRALIAN MATHEMATICS COMPETITION

Instructions and Information [ 0 0 0

You must maintain silence at all times. O O O O O O O O O O O

Do not open the paper until told to do so. O O O O O O O O O O O O O O O O O

Mobile phones are not allowed. If you have one you must give it to a supervisor now. O O O O O O O O O O O O O O O O O O O O O O O O O

You must not leave your seat during the competition. O O O O O O O O O O O

You may not borrow equipment without a supervisor's permission. O O O O O O O O O O O O O O O O O O O

If you wish to leave the room a supervisor must accompany you. O O O O O O O O O O O O O O O O O O

If you have any other questions, raise your hand and wait for a supervisor. O O O O O O O O O O O O O O O O O O O

You are allowed a working time of 75 minutes. There is no extra reading time. O O O O O O O O O O O O O O O O O O O O O

There are no penalties for incorrect answers. You should attempt all questions. O O O O O O O O O O O O O O O O

10.

The questions have been thoroughly checked. Each question stands as written and no further explanation can be provided.

O O O O O O O O O O O O O O O O O O O O O O O O O

11.

Diagrams are NOT drawn to scale. They are intended only as aids.

O O O O O O O O O O O O O O

12.

You may use printed language dictionaries.

O O O O O O O O O O O

13.

You may NOT use calculators.

O O O O O O O O

Important: No student may sit the competition more than once or sit more than one division of the competition. The AMT conducts integrity checks on competition results and reserves the right to withhold results or disqualify students if plagiarism or duplicate sittings are suspected. AUSTRALIAN MATHS TRUST

Level D Intermediate Grades 10-11

DATE

23 September

TIME ALLOWED

75 minutes

Intermediate Division

Questions 1 to 10 are worth 3 marks each.

1-10 题, 每题 3 分

A 40-minute lesson started at \( {10} : {50}\mathrm{\;{am}} \) . Exactly half-way through the lesson the fire alarm went off. At what time did the fire alarm go off?

一节时长为 40 分钟的课程从上午 10:50 开始。课程恰好进行到一半时, 火警报警器响了。请问火警报警器是在什么时间响起的?

(A) \( {10} : {30}\mathrm{\;{am}} \) (B) \( {11} : {00}\mathrm{\;{am}} \) (C) \( {11} : {10}\mathrm{\;{am}} \) (D) 11:20 am (E) \( {11} : {30}\mathrm{\;{am}} \)

Two rectangles have a vertex in common, as shown. What is the size of the angle marked \( {x}^{ \circ } \) between them? 如图所示, 两个长方形共用一个顶点。请问这两个长方形之间标记为 \( {x}^{ \circ } \) 角的度数是多少? (A) \( {10}^{ \circ } \) (B) \( {20}^{ \circ } \) (C) 30° (D) \( {40}^{ \circ } \) (E) \( {50}^{ \circ } \)

What is the value of \( \frac{2 + 3 + 4}{7 + 8 + 9} \) ?

请问 \( \frac{2 + 3 + 4}{7 + 8 + 9} \) 的值是多少?

(A) \( \frac{1}{6} \) (B) \( \frac{2}{7} \) (C) \( \frac{3}{8} \) (D) \( \frac{4}{9} \) (E) \( \frac{1}{2} \)

How many \( {25}\mathrm{\;{cm}} \times {25}\mathrm{\;{cm}} \) squares fit in a \( 1\mathrm{\;m} \) \( {50}\mathrm{\;{cm}} \times 1\mathrm{\;m} \) rectangle?

请问有多少个 \( {25}\mathrm{\;{cm}} \times {25}\mathrm{\;{cm}} \) 的正方形可 \( {50}\mathrm{\;{cm}} \) 以完全放入 \( {50}\mathrm{\;{cm}} \times 1\mathrm{\;m} \) 的长方形?

(A) 1 (B) 2 (C) 4

(D) 6 (E) 8

Which one of these is equal to \( {57} \times {953} \) ?

\( {57} \times {953} \) 与以下哪项值相等?

(A) 321 (B) 4321 (C) 54321 (D) 654321 (E) 7654321

A parallelogram \( {PQRS} \) has an area of \( {60}{\mathrm{\;{cm}}}^{2} \)

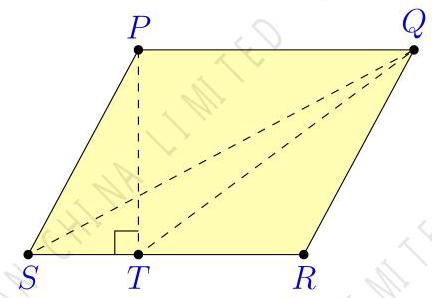
and side \( {PQ} \) of length \( {10}\mathrm{\;{cm}} \) .

Which length is \( 6\mathrm{\;{cm}} \) ?

如图所示,平行四边形 \( {PQRS} \) 的面积为

\( {60}{\mathrm{\;{cm}}}^{2} \) ,边 \( {PQ} \) 的长度为 \( {10}\mathrm{\;{cm}} \) 。

请问哪条线段的长度是 \( 6\mathrm{\;{cm}} \) ？

(A) \( {RQ} \) (B) \( {RS} \) (C) \( {QT} \) (D) \( {PT} \) (E) \( {QS} \)

Mei can travel to her grandma's house by a direct route, or by a scenic route that is \( 5\mathrm{\;{km}} \) longer. When she travels by the scenic route, and comes directly home, the round trip is \( {35}\mathrm{\;{km}} \) . How long is the direct route?

小梅可以选择一条直达路线或者选择一条风景优美的路线去奶奶家,风景优美的路线比直达路线长 \( 5\mathrm{\;{km}} \) 。如果她选择风景优美的路线去奶奶家并选择直达路线回家,来回路程一共为 \( {35}\mathrm{\;{km}} \) 。请问直达路线有多远?

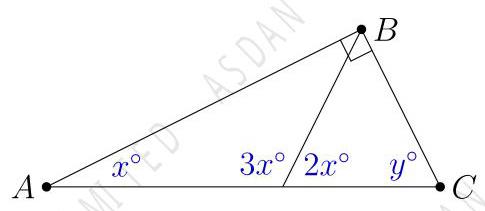
(A) \( 5\mathrm{\;{km}} \) (B) \( {12.5}\mathrm{\;{km}} \) (C) \( {15}\mathrm{\;{km}} \) (D) \( {20}\mathrm{\;{km}} \) (E) \( {22.5}\mathrm{\;{km}} \) 8. What is the value of \( {\left( {\left( {2}^{0}\right) }^{2}\right) }^{3} \) ? 请问 \( {\left( {\left( {2}^{0}\right) }^{2}\right) }^{3} \) 的值是多少? (A) 1 (B) 12 (C) 32 (D) 64 (E) 256 9. What must 0.05 be divided by to get 50 ? 请问 0.05 除以哪个数字才能得到 50? (A) 1000 (B) 100 (C) 0.1 (D) 0.001 (E) 0.0001 10. In the right-angled triangle \( {ABC} \) shown, what is the value of \( y \) ? 图中是一个直角三角形 \( {ABC} \) ,请问 \( y \) 的值是多少? (A) 45 (B) 48 (C) 54 (D) 60 (E) 72

Questions 11 to 20 are worth 4 marks each.

11-20 题, 每题 4 分

11.

The number 11 can be written as the sum of three positive whole numbers in many ways. In how many ways can this be done where the numbers are different and in increasing order?

数字 11 可以用多种方式表示为三个正整数之和。请问其中有多少种方式可以将 11 表示为三个升序排列的不同数字之和?

(A) 3 (B) 4 (C) 5 (D) 6 (E) 7

12.

A two-digit number is reversed then added to itself. The answer cannot be 一个两位数, 将它颠倒后再加上它本身。请问结果不可能是下列哪一项?

(A) 55 (B) 110 (C) 132 (D) 154 (E) 186

13.

Amy designed this rectangular flag for her fleet of yachts. What fraction of the flag is shaded?

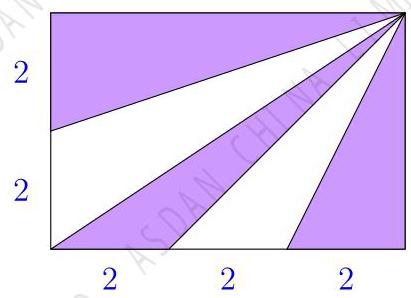
Amy 为游艇舰队设计了一面长方形旗帜。请问阴影部分的面积占旗帜总面积的几分之几?

(A) \( \frac{2}{3} \) (B) \( \frac{3}{5} \) (C) \( \frac{5}{8} \)

(D) \( \frac{1}{2} \) (E) \( \frac{7}{12} \)

14.

What is the largest possible whole-number value of the expression \( a \times b + \frac{c}{d} - \frac{e}{f} \) where \( a, b, c, d, e, f \) are the numbers1,2,3,4,5and 6 in some order?

已知 \( a \) 、 \( b \) 、 \( c \) 、 \( d \) 、 \( e \) 、 \( f \) 分别表示以某种顺序排列的数字 1、2、3、4、5 和 6,请问表达式 \( a \times b + \frac{c}{d} - \frac{e}{f} \) 的最大可能整数值是多少?

(A) 30 (B) 31 (C) 32 (D) 33 (E) 34

15.

Four children named, from youngest to oldest, Abdul, Bipin, Cai and Denise have ages which are equally spaced apart. Abdul and Bipin's ages add to 18 , whilst Cai and Denise's ages add to 34. How old is Denise?

四个小孩按照年龄从小到大的排列顺序分别是 Abdul、Bipin、Cai 和 Denise, 前后两个小孩的年龄之差都相等。Abdul 和 Bipin 的年龄之和为 18, Cai 和 Denise 的年龄之和为 34。请问 Denise 多少岁?

(A) 14 (B) 16 (C) 18 (D) 19 (E) 20

16.

The country of Exponentia uses six-digit telephone numbers. At the moment, this is plenty, since there are only 1000 phone numbers in use. However, increasing population and phone usage means that the number of phone numbers needs to double each year. Approximately how many years will it take for Exponentia to run out of phone numbers?

Exponentia 国家使用六位数的电话号码。目前, 这已经足够了, 因为只有 1000 个电话号码在使用。然而, 由于人口和电话使用量的增加, 电话号码的数量每年都需要翻倍。请问该国大约需要多少年可以用完所有的电话号码?

(A) 5 (B) 10 (C) 20 (D) 30 (E) 40

17.

A \( {15}\mathrm{\;{cm}} \times {15}\mathrm{\;{cm}} \) square of origami paper is dark blue on top and pale yellow underneath. The top-left corner is folded down so that a crease is made from the top-right corner to a point \( x\mathrm{\;{cm}} \) above the bottom-left corner.

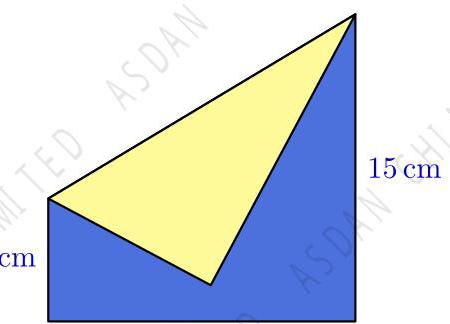
\( {15}\mathrm{\;{cm}} \)

Once folded, the visible regions of yellow and blue paper have equal areas. What is the value of \( x \) ?

一张 \( {15}\mathrm{\;{cm}} \times {15}\mathrm{\;{cm}} \) 的手工折纸,正面是深蓝色,背面是淡黄色。将纸张的左上角向下折,使折痕从右上角延伸到离左下角 \( x\mathrm{\;{cm}} \) 的位置。折好后,可见区域中黄色和蓝色纸张的面积相等。请问 \( x \) 的值是多少?

(E) \( 4\sqrt{2} \)

18.

In this equation, the coefficient of \( y \) has been hidden, but we know that it is a positive integer, 1 or more.

下面方程中, \( y \) 的系数被遮住了,已知这个系数是一个大于等于 1 的正整数。

\[ {2x} + y = {25} \]

The equation has at least one solution where \( x \) and \( y \) are positive integers.

How many different values are possible for the hidden coefficient?

这个方程至少有一个解,其中 \( x \) 和 \( y \) 为正整数。

请问被遮住的系数可能有多少个不同的值?

(A) 10 (B) 12 (C) 13 (D) 24 (E) 25

19.

Farmer Smith had a square property that he extended by buying a smaller square of land, creating the property shown.

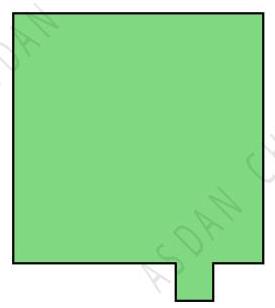
The new square of land increased the total perimeter of the property by \( {10}\% \) .

By what percentage did the area of the property increase? 农民 Smith 拥有一块正方形土地,他又购买了一块较小的正方形土地拓宽了原有的土地, 如图所示。新买的正方形土地使得土地的总周长增加了 10%。

请问土地的面积增加了百分之多少?

(A) 2 (B) 4 (C) 6 (D) 8 (E) 10

20.

I hear that dogs age 7 dog years every year. My dog Ruby was born on my ninth birthday. Four years from now, on our birthday, Ruby's age in dog years will be exactly four times my age in normal years. How old am I now?

据说, 人的一岁相当于狗龄的 7 岁。我的狗 Ruby 是在我九岁生日时出生的。再过四年我们过生日时, Ruby 的狗龄将恰好是我年龄的四倍。请问我现在多少岁?

(A) 10 (B) 12 (C) 13 (D) 15 (E) 17 Questions 21 to 25 are worth 5 marks each. 21-25 题,每题 5 分

21.

An ancient beast guards a \( 2\mathrm{\;{km}} \times 2\mathrm{\;{km}} \) square building on an otherwise featureless plain.

A 4 km-long unbreakable chain connects the beast to the outside wall of the building, as shown in the diagram. Neither the beast nor the chain can cross into the area occupied by the building.

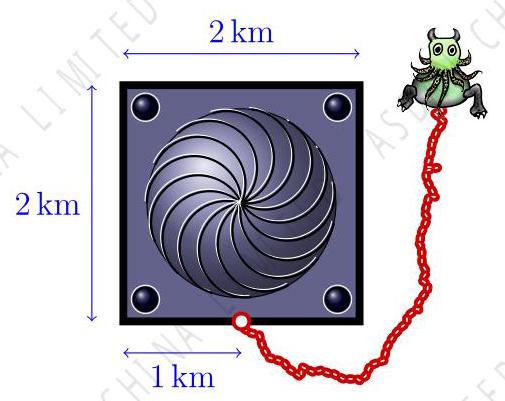
What is the area that the beast can access,

in square kilometres?

一只古兽守卫着荒原上一座 \( 2\mathrm{\;{km}} \times 2\mathrm{\;{km}} \) 的方形建筑。如图所示,一条长度为 \( 4\mathrm{\;{km}} \) 的牢固锁链将古兽与建筑物外面的墙连在一起。古兽和锁链都不能进入建筑物占据的区域。请问古兽可以活动的区域是多少平方千米?

(A) \( {9\pi } \) (B) \( {10\pi } \) (C) \( {11\pi } \) (D) \( {12\pi } \) (E) \( {13\pi } \)

22.

I have four numbers. When I add 3 to the first number, subtract 3 from the second number, multiply the third number by 3 and divide the fourth number by 3 , my four answers are all equal.

My original 4 numbers added to 32 . What is the sum of the largest two of these? 有四个数字。将第一个数字加上 3 ,第二个数字减去 3 ,第三个数字乘以 3 ,第四个数字除以 3 ,得到的四个结果都相等。

已知原来的四个数字之和为 32 , 请问原来的四个数字中最大的两个数字之和是多少?

(A) 24 (B) 25 (C) 26 (D) 27 (E) 28 23. These two rectangular prisms have the same surface area. Both \( x \) and \( y \) are integers less than 10 . What is \( x + y \) ? 右图中两个长方体的表面积相等,其中 \( x \) 和 \( y \) 都是小于 10 的整数。请问 \( x + y \) 的值是多少?

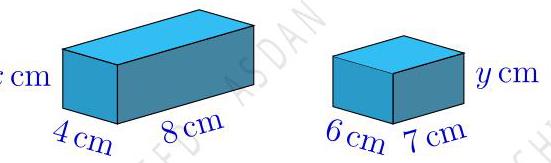
(A) 5 (B) 7 (C) 11 (D) 12 (E) 13

24.

Sometimes a three-digit number is an exact multiple of its digit sum. For instance, the digit sum of 102 is \( 1 + 0 + 2 = 3 \) and \( {102} = 3 \times {34} \) . If a three-digit number is \( k \) times the sum of its digits, what is the smallest possible integer value of \( k \) ?

有时一个三位数是它的各位数字之和的整数倍。例如, 102 的各位数字之和是 1 + \( 0 + 2 = 3 \) ,且 \( {102} = 3 \times {34} \) 。如果一个三位数是它的各位数字之和的 \( k \) 倍,请问整数 \( k \) 的最小可能值是多少?

(A) 9 (B) 10 (C) 11 (D) 12 (E) 13

25.

Six identical equilateral triangles of side length 2 are drawn outside a regular hexagon of side length 1 , defining a larger hexagon as shown.

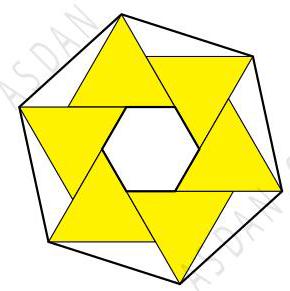
What is the ratio of the area of the larger hexagon to the area of the smaller hexagon? 如图所示,在边长为 1 的正六边形外侧绘制六个相同的边长为 2 的等边三角形, 从而构成一个更大的六边形。请问大六边形的面积与小六边形的面积之比是多少?

(A) \( 5 : 1\; \) (B) \( 6 : 1\; \) (C) \( 7 : 1\; \) (D) \( 8 : 1\; \) (E) \( 9 : 1 \)

For questions 26 to 30, colour in the bubbles on the answer sheet to record whole-number answers from 0 to 999 . Questions 26 to 30 are worth

6,7,8,9and10marks respectively.

26 题至 30 题的答案为 0 至 999 的整数, 请正确填涂在答题卡上。第 26 题占 6 分, 第 27 题占 7 分,第 28 题占 8 分,第 29 题占 9 分,第 30 题占 10 分。

26.

Seána was arranging her collection of postage stamps into groups when a cat jumped onto them and scattered the stamps. All she can remember is that when she put them into groups of2,3,4,5or 6 she always had 1 stamp left over. When she placed them into groups of 7 there were none left over.

What is the minimum number of stamps Seána could have had in her collection? 小娜正在将收集到的邮票分组, 这时一只猫跳到邮票上面弄乱了邮票。小娜只记得她将邮票以 2 张、3 张、4 张、5 张或者 6 张分为一组时,总会剩下 1 张邮票, 但将邮票分成 7 张一组时, 不会剩下邮票。

请问小娜至少收集了多少张邮票?

27.

A square \( {ABCD} \) is inscribed in a right-angled triangle \( {EFG} \) as shown.

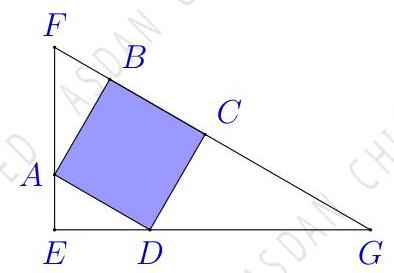
The length of \( {EG} \) is 4 units and the length of \( {EF} \) is 3 units.

As a fraction in simplest form, the side-length of the square is \( \frac{a}{b} \) . What is the value of \( a + b \) ?

如图所示,正方形 \( {ABCD} \) 内接于一个直角三角形 \( {EFG} \) 中。 \( {EG} \) 的长度为 4 个单位, \( {EF} \) 的长度为 3 个单位。正方形的边长可以表示为最简分式 \( \frac{a}{b} \) 。请问 \( a + b \) 的值是多少?

28.

The elves have to choose who will go the annual magic conference. They sit in a circle and the chief elf Elvin starts counting round the circle, starting with himself. Every second elf counted drops out of the circle and the counting continues until Elvin drops out. All those left in the circle go to the conference.

This year, there are 1000 elves in the circle. How many will go to the conference? 小精灵们需要选出即将参加年度魔法盛会的精灵。所有精灵围成一个圆圈坐下, 精灵首领 Elvin 从自己开始沿着圆圈数数, 每数到第二个的精灵离开圆圈, 直到 Elvin 离开圆圈时,停止数数。所有留在圆圈中的精灵都将参加盛会。

今年,一共有 1000 只精灵围成一个圆圈坐下。请问有多少只精灵将参加盛会？

29.

Two wheels are fixed to an axle as shown. Due to their different sizes, the two wheels trace two concentric circles when rolled on level ground.

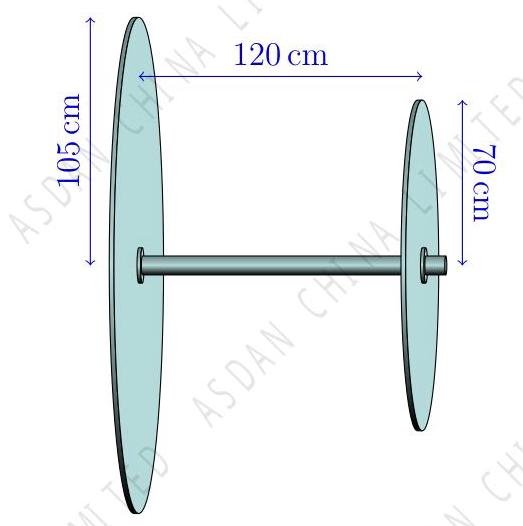
In centimetres, what is the radius of the circle traced on the ground by the larger wheel?

如图所示,两个车轮固定在一个车轴上。

车轮在水平地面滚动时, 由于其尺寸不同, 这两个车轮会划出两个同心圆。请问大车轮在地面上划过的圆的半径是多少厘米?

30.

A tromino is a shape made from three squares traced on gridlines. A \( 2 \times 3 \) grid can be tiled by trominoes in exactly three ways, as shown.

三格骨牌是在网格线上绘制三个正方形组成的形状。如图所示,一个 \( 2 \times 3 \) 网格恰好可以通过三种方式用三格骨牌平铺而成。

We count two tilings that are reflections of each other as different. Similarly, two tilings that are rotations of each other are counted as different.

In how many different ways can a \( 3 \times 6 \) grid be tiled by trominoes?

我们将两个对称的平铺方式看作是不同的方式。同样, 旋转后相同的平铺方式也看作是不同的方式。

请问用三格骨牌平铺构成 \( 3 \times 6 \) 网格一共有多少种不同的方式?