Intermediate Division

Questions 1 to 10,3 marks each

第 1-10 题, 每题 3 分

What is the value of \( \left( {{57} \times {346}}\right) + \left( {{43} \times {346}}\right) \) ?

请问 \( \left( {{57} \times {346}}\right) + \left( {{43} \times {346}}\right) \) 的值是多少?

(A) 14878 (B) 19722 (C) 31500 (D) 34600 (E) 46300

Of the following, which is closest to 14?

请问下列哪个数字最接近 14?

(A) 14.4 (B) 13.84 (C) 14.14 (D) 13.68 (E) 14.21

The average of 2024 and an unknown number is \( 2\frac{1}{2} \) . What is the unknown number? 2024 与一个未知数的平均数为 \( 2\frac{1}{2} \) 。请问这个未知数是多少?

What is the value of \( x \) in the diagram? 请问图中 \( x \) 的值是多少?

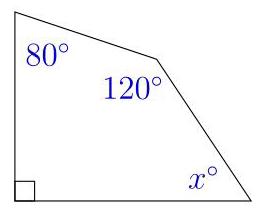
(A) 40 (B) 50 (C) 60 (D) 70 (E) 80

What is the area of the shape drawn in the grid? 请问网格中图形的面积是多少? (A) 7 (B) 8 (C) 9 (D) 10 (E) 11

The largest integer \( n \) for which \( {0.6n} \) is less than 17 is

若 \( {0.6n} \) 小于 17,请问整数 \( n \) 的最大值是多少?

(A) 9 (B) 10 (C) 11 (D) 26 (E) 28

Let \( p \) be \( {12}\% \) of 300 and \( q \) be \( 6\% \) of 600 . What is the difference between \( p \) and \( q \) ? 设 \( p \) 为 300 的 \( {12}\% , q \) 为 600 的 \( 6\% \) 。请问 \( p \) 和 \( q \) 之间的差值是多少?

(A) 0 (B) 2 (C) 6 (D) 12 (E) 30

Pat has \( {12}\mathrm{{eggs}},2\mathrm{\;{kg}} \) of flour, and \( 2\mathrm{\;L} \) of milk. His pancake recipe calls for \( 2\mathrm{{eggs}},{250}\mathrm{\;g} \) of flour and \( {400}\mathrm{\;{mL}} \) of milk. He makes as many pancakes as he can while using the ingredients in the proportions given in the recipe. How much flour will he have left? Pat 有 12 个鸡蛋、 \( 2\mathrm{\;{kg}} \) 面粉和 \( 2\mathrm{\;L} \) 牛奶。他的煎饼菜谱上标明制作一个煎饼需要 2 个鸡蛋、 \( {250}\mathrm{\;g} \) 面粉和 \( {400}\mathrm{\;{mL}} \) 牛奶。如果他按照菜谱上的原材料比例制作尽可能多的煎饼, 请问他会剩下多少面粉?

(A) None 没有剩余 (B) \( {250}\mathrm{\;g} \) (C) \( {500}\mathrm{\;g} \) (D) \( {625}\mathrm{\;g} \) (E) \( {750}\mathrm{\;g} \)

Theo's collection of toy dinosaurs is stored in two containers. He noticed that one of the containers had 4 times as many dinosaurs in it as the other. He moved 15 to the other container so that the two containers had the same number. How many dinosaurs are in Theo's collection?

Theo 将恐龙玩具收纳在两个箱子中。他注意到其中一个箱子的恐龙玩具数量是另一个箱子的 4 倍, 因此他从装有更多玩具的箱子中拿出 15 个玩具放到另一个箱子中, 使得两个箱子中的恐龙玩具数量相同。请问 Theo 有多少个恐龙玩具?

(A) 40 (B) 45 (C) 50 (D) 55 (E) 60

10.

Eiliyah is drawing an isosceles triangle on the number plane. It has an area of 6 square units. She has already plotted two vertices of the triangle, at (1,1)and(3,1). Which of the following could be the coordinates of the third vertex of the triangle? Eiliyah 正在坐标平面上绘制一个面积为 6 个平方单位的等腰三角形。她已经标记出这个等腰三角形的两个顶点(1,1)和(3,1)。请问下列哪一项可能是这个等腰三角形的第三个顶点坐标?

(A)(2, - 3) (B)(2, - 5) (C)(2,3) (D)(2,4) (E)(2,6)

Questions 11 to 20, 4 marks each 第 11-20 题,每题 4 分

11.

How many digits are in the number \( {202}^{4} \) ?

请问 \( {202}^{4} \) 中有多少位数字？

(A) 7 (B) 10 (C) 12 (D) 18 (E) 81

12.

Yalis has to take a tablet every 9 hours. The course of medication is 15 tablets. He takes his first tablet at 11 am on Tuesday. When will he take his last tablet?

Yalis 需要每 9 个小时服用 1 片药, 整个疗程一共需要服用 15 片药。他在周二上午 11 点服用了第 1 片药。请问他将在什么时候服用最后 1 片药?

(A) \( 2\mathrm{{pm}} \) Wednesday 周三下午 2 点

(B) \( 5\mathrm{\;{am}} \) Friday 周五凌晨 5 点

(D) 4 am Monday 周一凌晨 4 点

(E) \( 8\mathrm{{pm}} \) Tuesday 周二晚上 8 点

13.

In the diagram, the concentric circles are equally spaced, with radii from 1 to 6 , and the lines from the origin are equally spaced \( {20}^{ \circ } \) apart. Which of these five areas is largest?

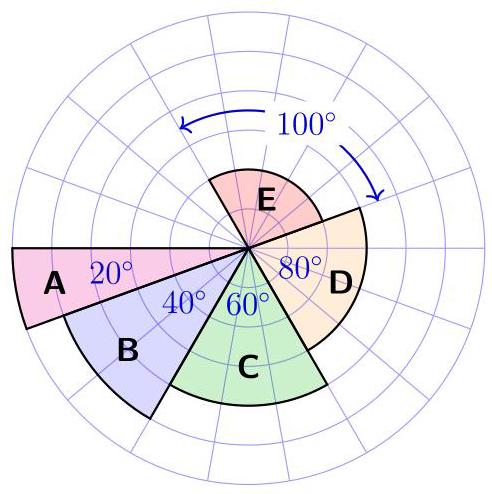
如图所示, 所有同心圆等距排列, 各圆半径从里到外依次从 1 递增到 6 。从圆心引出的各线段之间的夹角均为 \( {20}^{ \circ } \) 。请问以下 5 个区域中, 哪个区域面积最大?

(A) A (B) B (C) C (D) D (E) E

14.

Kate and Jim exercise at their local beach, going from one end to the other and back. Starting together, Kate jogs at a steady pace of \( {10}\mathrm{\;{km}} \) per hour, while Jim walks at \( 6\mathrm{\;{km}} \) per hour. They first meet again after 30 minutes. How long, in kilometres, is the beach? Kate 和 Jim 在沙滩上锻炼身体, 从一端到另一端再返回。两人同时出发, Kate 按照 \( {10}\mathrm{\;{km}}/\mathrm{h} \) 的速度匀速慢跑,而 \( \mathrm{{Jim}} \) 按照 \( 6\mathrm{\;{km}}/\mathrm{h} \) 的速度行走,出发 30 分钟后两人第一次相遇。请问这个沙滩长多少 \( \mathrm{{km}} \) ？

(A) 4 (B) 5 (C) 6 (D) 7 (E) 8

15.

A game uses the two spinners shown. The player who spins the higher number wins. Equal spins are a draw. What is the probability that player one wins?

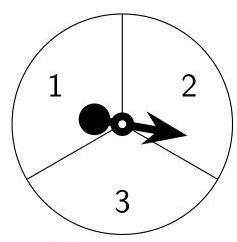
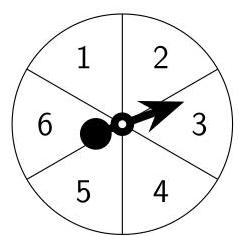
Player one Player two

1 号玩家 2 号玩家

游戏采用如图所示两个转盘, 转到较大数字的玩家获胜。如果两位玩家转出的结果相同则为平局, 请问 1 号玩家获胜的概率是多少?

(A) \( \frac{1}{2} \) (B) \( \frac{1}{3} \) (C) \( \frac{1}{6} \) (D) \( \frac{2}{3} \) (E) \( \frac{5}{6} \)

16.

When the number 9045 is split into two 2-digit numbers, the first number is twice the second number: \( {90} = 2 \times {45} \) . Many other 4-digit numbers can be split into two 2-digit numbers where the first number is twice the second. There is a unique 2-digit number that divides into all such 4-digit numbers. What is this number?

将数字 9045 分成两个 2 位数后,第一个数是第二个数的两倍,即 \( {90} = 2 \times {45} \) 。还有很多类似的 4 位数可以分为两个 2 位数, 且第一个 2 位数是第二个 2 位数的两倍。存在唯一一个 2 位数, 能整除所有类似的 4 位数。请问这个 2 位数是多少?

(A) 18 (B) 35 (C) 45 (D) 52 (E) 67

17.

This star has order-10 rotational symmetry, with 10 internal right angles as shown. What is the size of each of the obtuse angles

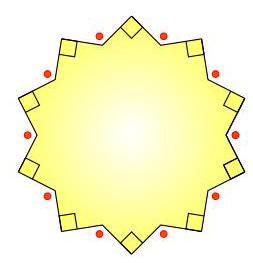
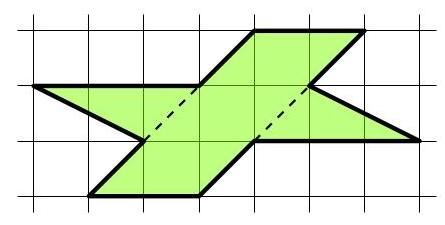
marked with a dot?

如图所示,此星形是 10 阶旋转对称图形,有 10 个内直角。请问图中每个用圆点标记的钝角为多少度?

(A) 120° (B) 126° (C) 132° (D) 138° (E) 142°

18.

I make up all the 5-digit numbers that use each of the digits from 1 to 5 once. I then arrange these 120 numbers in increasing order from 12345 to 54321 . Which number is the 42nd in this order?

数字 1 到 5 可以组成 120 个不同的 5 位数, 其中每个数字只使用一次。然后将这些数从 12345 到 54321 升序排列。请问按此顺序,第 42 个数是什么？

(A) 15234 (B) 21354 (C) 23154 (D) 24531 (E) 24513

19.

Triangle \( {ABC} \) has a right angle at \( A \) , and side \( {AC} \) is twice as long as \( {AB} \) . Also \( {MN} \) is the perpendicular bisector of \( {BC} \) , as shown.

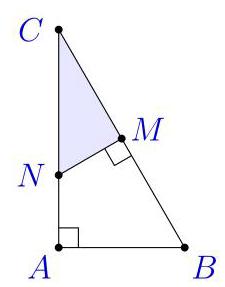
In area, what fraction of \( \bigtriangleup {ABC} \) is \( \bigtriangleup {CMN} \) ?

在三角形 \( {ABC} \) 中, \( \angle A \) 为直角。 \( {AC} \) 边长度是 \( {AB} \) 边长度的两倍。 \( {MN} \) 是 \( {BC} \) 边的垂直平分线,如图所示。请问 \( \bigtriangleup {CMN} \) 的面积占 \( \bigtriangleup {ABC} \) 面积的几分之几?

(A) \( \frac{1}{3} \) (B) \( \frac{1}{\sqrt{5}} \) (C) \( \frac{2}{5} \) (D) \( \frac{\sqrt{5}}{8} \) (E) \( \frac{5}{16} \)

20.

A researcher surveys 10 households and creates this scatterplot showing how many people and how many internet-connected devices are in each house.

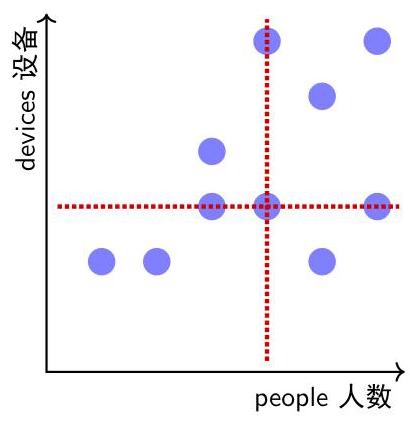
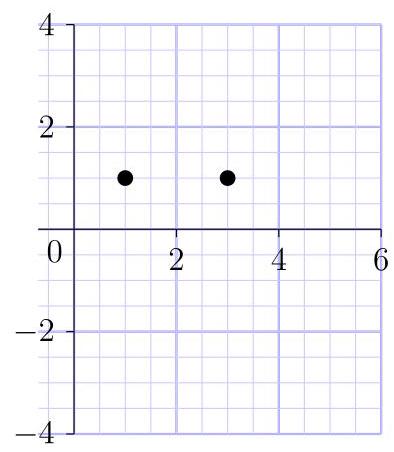
一位研究人员对 10 个家庭进行了调研, 并根据其调研结果绘制了如图所示的散点图, 表示每个家庭中的人数与联网设备数量之间的关系。

To help categorise her data, she adds a vertical line representing the median number of people and a horizontal line representing the median number of devices.

为了将数据分类, 她在图中加入一条垂直线表示人数的中位数, 又加入一条水平线表示设备数量的中位数。

One extra household is surveyed and the results are added to the scatterplot. What will happen to the median lines?

现在对另一个家庭进行调研, 调研结果最终会表示在这个散点图中。请问图中两条中位线将会有何变化?

(A) Both lines move. 两条线都会移动。

(B) Neither line moves. 两条线都不会移动。

(D) Only the horizontal line moves. 只有水平线会移动。

(E) It depends on the location of the new point. 取决于新加入点的位置。

Questions 21 to 25, 5 marks each 第 21-25 题, 每题 5 分

21.

February 2024 had 5 Thursdays. When will February next have 5 Thursdays?

2024 年 2 月有 5 个周四。请问接下来哪一年的 2 月将再次出现 5 个周四?

22.

A group of tourists stayed in two rooms when visiting a museum. The average age of the tourists in the first room was 45 and the average age of the tourists in the second room was 20. When one tourist walked from the first room to the second, the average ages in each room increased by 1 . If the second group had 7 more tourists at the beginning, what was the age of the tourist who moved rooms?

参观博物馆时, 一群游客分别在两个房间里。第一个房间里游客的平均年龄是 45 岁; 第二个房间里游客的平均年龄是 20 岁。如果某位游客从第一个房间走到第二个房间, 那么每个房间里游客的平均年龄都会增加 1 岁。如果刚开始时, 第二个房间比第一个房间多 7 位游客, 请问从第一个房间走到第二个房间的游客的年龄是多少岁?

(A) 36 (B) 37 (C) 38 (D) 39 (E) 40

23.

A tank in the shape of a rectangular prism has dimensions as shown. It contains water to a depth of \( {12}\mathrm{\;{cm}} \) . A solid cube of side \( {20}\mathrm{\;{cm}} \) is placed into the tank, with one face flat on the bottom of the tank. By how much will the water level in the tank increase?

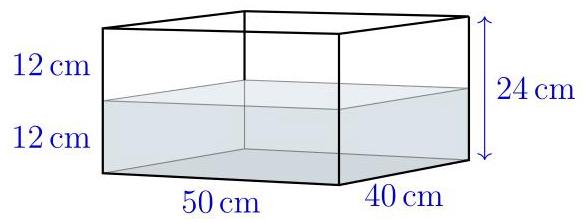
一个长方体水缸的尺寸如图所示。水缸中的水深为 \( {12}\mathrm{\;{cm}} \) 。将一个边长为 \( {20}\mathrm{\;{cm}} \) 的实心立方体平放在缸底,请问此时水缸中的水位会上涨多少 \( \mathrm{{cm}} \) ?

(A) \( 3\mathrm{\;{cm}} \) (B) \( 4\mathrm{\;{cm}} \) (C) \( 5\mathrm{\;{cm}} \) (D) \( 8\mathrm{\;{cm}} \) (E) \( {12}\mathrm{\;{cm}} \)

24.

Six maths students, Amy, Bao, Cecil, Daria, Emilia and Felipe are given 60 problems to complete over the weekend. Although none of them completes all 60, each completes at least 52 of the problems, and each one completes a different number of problems. Also the order from least to most problems is the same as the alphabetical order of their names. Amy、Bao、Cecil、Daria、Emilia、Felipe 6 位学生需要在本周末完成 60 道题。虽然她们都没有将这 60 道题全部完成, 但是每个人都至少完成了其中 52 道题且每个人完成的题目数量不同。同时, 如果将这 6 位学生的题目完成数量从最少到最多进行排序, 结果刚好与这 6 位学生的名字按字母表顺序进行排序的结果相同。

Finally, each of them completes \( k \) times as many problems on Saturday as they do on Sunday, where \( k \) is a different whole number from 1 to 6 for each of them. Which of them completed 3 times as many problems on Saturday as on Sunday?

最终,每位学生周六完成的题目数量都是其周日完成的题目数量的 \( k \) 倍。其中 \( k \) 是 1 到 6 之间的一个整数,且每位学生对应的 \( k \) 值不同。请问哪一位学生在周六完成的题目数量是周日的 3 倍?

(A) Amy (B) Bao (C) Cecil (D) Daria (E) Emilia

25.

Abi is walking beside a lake. In the distance she can see a tree and its reflection on the surface of the lake. There is a depth indicator 5 metres away from her with its 0 -metre mark at the lake surface level.

Abi 在湖边散步。在某个距离,她刚好能看到一棵树和树在湖面的倒影。在距离她 \( 5\mathrm{\;m} \) 处有一个深度标尺,湖面高度刚好达到 \( 0\mathrm{\;m} \) 刻度处。

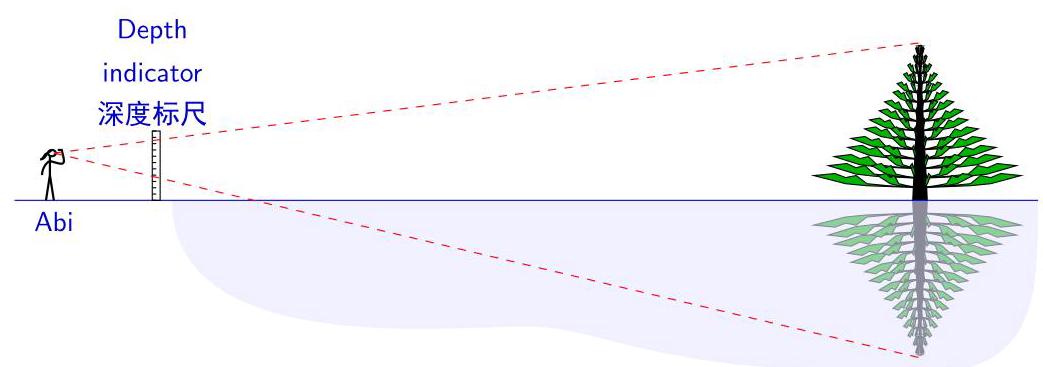
From Abi's point of view, the top of the tree is in line with the 1.8-metre mark on the depth indicator, while the reflection of the top of the tree is in line with the 1.1-metre mark. Abi's eyes are level with the 1.5-metre mark. How tall is the tree in metres?

从 \( \mathrm{{Abi}} \) 的视角看,树的顶部刚好与深度标尺 \( {1.8}\mathrm{\;m} \) 刻度处齐平,而树的倒影的顶部与深度标尺 \( {1.1}\mathrm{\;m} \) 刻度处齐平。Abi 的眼睛与深度标尺 \( {1.5}\mathrm{\;m} \) 刻度处齐平。请问这棵树高多少米?

(A) 9 (B) 9.5 (C) 10 (D) 10.5 (E) 11

For questions 26 to 30, shade the answer as an integer from 0 to 999

in the space provided on the answer sheet.

第 26-30 题的答案为 0-999 之间的整数,请将答案填涂在答题卡对应区域。

Questions 26-30 are worth 6, 7, 8, 9 and 10 marks, respectively. 第 26-30 题分别为 6,7,8,9,10 分。 26. In the multiplication puzzle shown, \( a, b \) and \( c \) represent different digits. 下方所示乘法竖式中, \( a\text{、}b\text{、}c \) 代表不同数字。

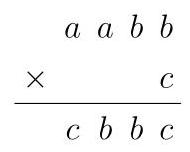
There are two different solutions to this puzzle. What is the difference between the two possible three-digit numbers of the form abc?

有两种不同解法可以满足上述条件。请问两个可能的三位数 \( {abc} \) 之差是多少？

27.

Rodney builds increasingly large shapes out of unit rods. The smallest uses six rods and each larger shape adds a layer of hexagons around the previous shape.

Rodney 使用单位长度的棍子构建图形, 且这些图形逐渐增大。最小的图形使用六根棍子,之后的每个图形都是通过在前一个图形周围加一层六边形构建而成的。

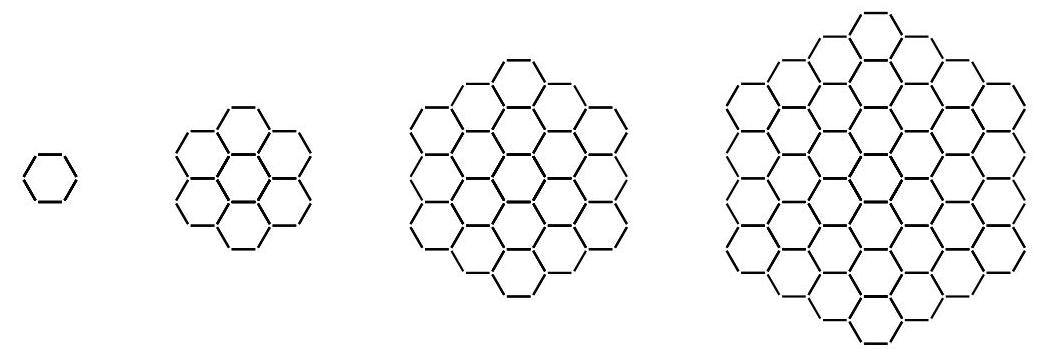
Starting with 2000 rods, Rodney builds a single shape like this, as large as possible. How many rods will he have left over?

Rodney 使用 2000 根棍子构建一个尽可能大的图形。请问他最后还能剩下多少根棍子？

28.

Let \( x, y \) and \( z \) be positive integers satisfying the following three equations:

设 \( x\text{、}y\text{、}z \) 为满足下列 3 个方程的正整数:

\[ {xy} + x + y = {2024} \]

\[ {yz} + y + z = {2024} \]

\[ {zx} + z + x = {624}. \]

What is the value of \( x + y + z \) ?

请问 \( x + y + z \) 的值是多少?

29.

Tim uses plug-in timers to automate his indoor plant lighting. Each timer has a plug on the back, a socket on the front, and a motorised dial that rotates once for every 24 hours that the plug has power.

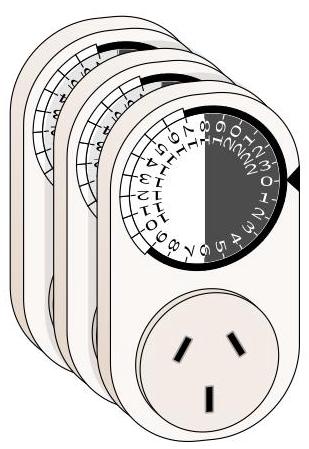
Tim 用插电式定时器来实现室内植物补光灯的自动化。每个定时器的背面都有插头, 正面有插座, 附带一个电动表盘。定时器插电后, 电动表盘每 24 小时转一圈。

When the time on the dial is between 9:00 and 17:00, the timer switch is on, so that any power on the plug is switched through to the socket. 当表盘上的时间介于 9:00 到 17:00 之间时,定时器开启,此时插座接通电源。

For fun, he plugs together three of his timers, all set to time 0:00 , with a lamp plugged into the front socket. How many hours until the lamp turns on?

Tim 做了一个有趣的实验。他将 3 个时间设置为 0:00 的定时器串联起来,并将一盏台灯插入定时器正面的插座。请问需要多少个小时才能点亮这盏台灯？

30.

A triangle, \( \bigtriangleup {ABC} \) , has sides \( {AB} = {12},{AC} = {16} \) , and \( {BC} = {20} \) . Point \( P \) is on side \( {AB} \) and a line is drawn through \( P \) so that half of the perimeter of \( \bigtriangleup {ABC} \) lies on each side of the line and half of the area of \( \bigtriangleup {ABC} \) lies on each side of the line. What is the square of the distance \( {CP} \) ?

在三角形 \( \bigtriangleup {ABC} \) 中, \( {AB} = {12},{AC} = {16},{BC} = {20} \) 。点 \( P \) 位于 \( {AB} \) 边上,过点 \( P \) 作一条直线,这条直线将 \( \bigtriangleup {ABC} \) 的周长和面积分别平分。请问 \( {CP} \) 长度的平方是多少?

澳大利亚AMC-10年级D

Intermediate Division

Questions 11 to 20, 4 marks each 第 11-20 题,每题 4 分

Questions 21 to 25, 5 marks each 第 21-25 题, 每题 5 分