中级组

第1–10题，每题3分

第 1-10 题, 每题 3 分 1. \( \left( {{57} \times {346}}\right) + \left( {{43} \times {346}}\right) \) 的值是多少？ (A) 14878 (B) 19722 (C) 31500 (D) 34600 (E) 46300

根据分配律，\( \left( {{57} \times {346}}\right) + \left( {{43} \times {346}}\right) = \left( {{57} + {43}}\right) \times {346} = {100} \times {346} = {34600} \)，故选(D)。

(A) 14.4 (B) 13.84 (C) 14.14 (D) 13.68 (E) 14.21

小于14的数中最大的是13.84，大于14的数中最小的是14.14，后者更接近14，故选(C)。

(A) 2019 (B) -2019 (C) 2029 (D) -2029 (E) -2024

两数之和为\( 2 \times \left( {2\frac{1}{2}}\right) = 5 \)，故未知数为\( 5 - {2024} = - {2019} \)，故选(B)。

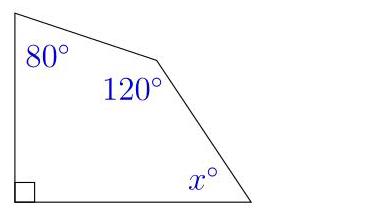
(A) 40 (B) 50 (C) 60

(D) 70 (E) 80

解法一

四边形内角和为\( {360}^{ \circ } \)，因此\( x = {360} - {90} - {80} - {120} = {70} \)，

故选(D)。

方案2

再添加一条竖直线后，可求出\( {100}^{ \circ } \)的同旁内角，继而得到\( {20}^{ \circ } \)角，最后求出\( {x}^{ \circ } = {90}^{ \circ } - {20}^{ \circ } = {70}^{ \circ } \)的角，因此选(D)。

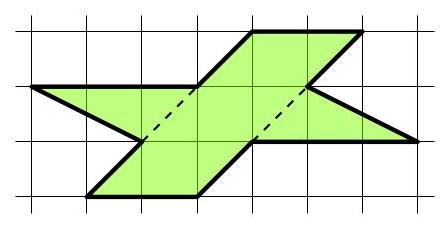
数网格方格或利用平行四边形面积为\( 2 \times 3 + 1 \times 3 = 9 \)，因此选(C)。

__________

(A) 9 (B) 10 (C) 11 (D) 26 (E) 28

要满足\( {0.6n} = {17} \)需\( n = {17} \div {0.6} = {170} \div 6 = {28}\frac{1}{3} \)。对于任何不超过28的\( n \)，\( {0.6n} \)的值均小于17，因此最大的该整数为\( n = {28} \)，

故选(E)。

__________

(A) 0 (B) 2 (C) 6 (D) 12 (E) 30

\( p = {12} \times \left( {1\% \times {300}}\right) = {12} \times 3 = {36} \)与\( q = 6 \times \left( {1\% \times {600}}\right) = 6 \times 6 \)。于是\( p - q = 0 \)，因此选(A)。

他按配方比例尽可能多地制作煎饼。

他将剩下多少面粉？

(A) 无 (B) \( {250}\mathrm{\;g} \) (C) \( {500}\mathrm{\;g} \)

(D) \( {625}\mathrm{\;g} \) (E) \( {750}\mathrm{\;g} \)

设一份“批次”煎饼的配方用量。他有足够的鸡蛋做6批，足够的面粉做8批，足够的牛奶做5批。因此做完5批后牛奶用完，还剩\( 2 - 5 \times {0.25} = {0.75}\mathrm{\;{kg}} = {750}\mathrm{\;g} \)面粉，

故选(E)。

西奥的收藏共有多少只恐龙？

(A) 40 (B) 45 (C) 50 (D) 55 (E) 60

每10只恐龙，移动前一只盒子里有2只，另一只有8只；移动后每只盒子各有5只。因此每10只恐龙，他移动了3只。

由于他实际移动了\( 5 \times 3 = {15} \)，他的收藏共有\( 5 \times {10} = {50} \)只恐龙，故选(C)。

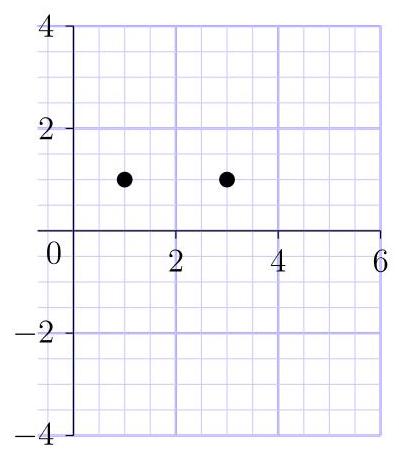
下列哪个可能是三角形第三个顶点的坐标？

(A)(2, - 3) (B)(2, - 5) (C)(2,3)

(D)(2,4) (E)(2,6)

以\( A = \left( {1,1}\right) \)与\( B = \left( {3,1}\right) \)之间的线段为底，长度为2，则高必须为6。因此第三个顶点\( C \)位于直线\( y = 7 \)或直线\( y = - 5 \)上。

在给定点中，只有\( C = \left( {2, - 5}\right) \)可行，且它位于线段\( {AB},\bigtriangleup {ABC} \)的垂直平分线上，故为等腰三角形，因此选(B)。2024澳大利亚数学竞赛第11-20题，每题4分 第11-20题,每题4分 11. 数字\( {202}^{4} \)有多少位？ (A) 7 (B) 10 (C) 12 (D) 18 (E) 81

解法一

估算得\( {202}^{4} > {200}^{4} = {2}^{4} \times {10}^{8} = {1600000000} \)，因此\( {202}^{4} \)至少有10位，且极可能恰好10位。验证得\( {202}^{4} < {300}^{4} = {8100000000} \)为10位数，故选(B)。解法二 \( {202}^{4} = {2}^{4} \times {101}^{4} = {16} \times {104060401} = {1664966416} \)，共10位，故选(B)。

(A) \( 2\mathrm{{pm}} \) 星期三 (B) 周五上午5点 (C) 周日下午5点

(D) 周一凌晨4点 (E) \( 8\mathrm{{pm}} \) 星期二

任意两片药之间间隔9小时，因此第1片到第15片之间有14个9小时的间隔，共\( 9 \times {14} = {126} \)小时。由于\( {126} \div {24} = 5 \)除以24余6，所以时间落在第一片药后第5天的周日\( 5\mathrm{{pm}} \)，

故选(C)。

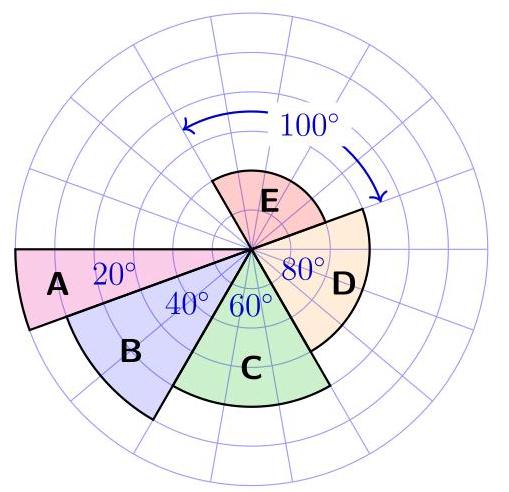
这五个区域中哪一个面积最大？

(A) A (B) B (C) C

(D) D (E) \( \mathrm{E} \)

半径为\( r \)、圆心角为\( {\theta }^{ \circ } \)的扇形面积为\( \pi {r}^{2} \times \frac{\theta }{360} \)。因此各区域面积为

\[

\]

\[

\]

\[

\]

\[

\]

\[

\]

\[

\]

\[

\]

\[

\]

\[

\]

\[

\]

故选(B)。

(A) 4 (B) 5 (C) 6 (D) 7 (E) 8

30分钟内，凯特跑了\( 5\mathrm{\;{km}} \)，而\( J\mathrm{\;{im}} \)走了\( 3\mathrm{\;{km}} \)，因此凯特必定已到达海滩尽头折返，并在回程中与吉姆相遇，多走了\( 2\mathrm{\;{km}} \)。于是他们在距海滩尽头\( 1\mathrm{\;{km}} \)处相遇，海滩全长\( 4\mathrm{\;{km}} \)，

故选(A)。

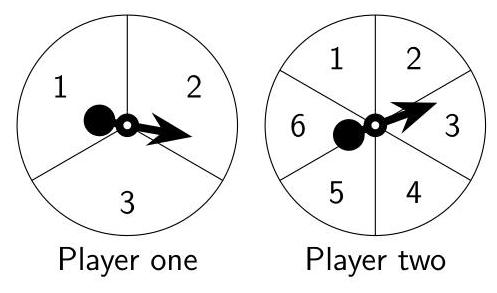
玩家一获胜的概率是多少？

(A) \( \frac{1}{2} \) (B) \( \frac{1}{3} \) (C) \( \frac{1}{6} \) (D) \( \frac{2}{3} \) (E) \( \frac{5}{6} \)

解法1

若玩家1掷出1，则玩家2有5/6的获胜概率，双方皆不获胜的概率为1/6，玩家1获胜的概率为0。

若玩家1掷出2，则玩家2有2/3的获胜概率，双方皆不获胜的概率为1/6，玩家1获胜的概率为1/6。

若玩家1掷出3，则玩家2有1/2的获胜概率，双方皆不获胜的概率为1/6，玩家1获胜的概率为\( 1/3 \)。

玩家1获胜的概率为\( 1/3 \times 0 + 1/3 \times 1/6 + 1/3 \times 1/3 = 1/6 \)，

故选(C)。

解法2

在18个等可能的(玩家1,玩家2)组合中，仅\( \left( {2,1}\right) ,\left( {3,1}\right) \)与(3,2)使玩家1获胜。因此玩家1获胜的概率为\( \frac{3}{18} = \frac{1}{6} \)，故选(C)。

存在一个唯一的两位数，能整除所有这样的四位数。这个数是多少？

(A) 18 (B) 35 (C) 45 (D) 52 (E) 67

可能的数为\( {2010},{2211},{2412},{2613},\ldots ,{9849} \)。它们分别是\( {201} \times {10},{201} \times {11},\ldots \)、\( {201} \times {49} \)。因此\( {201} = \gcd \{ \left( {{2010},{2211},{2412},{2613},\ldots ,{9849}}\right) \} \)是所有可能数的最大公约数。其质因数分解为\( {201} = {67} \times 3 \)，故67是唯一一个能整除所有这些数的两位数，

故选(E)。

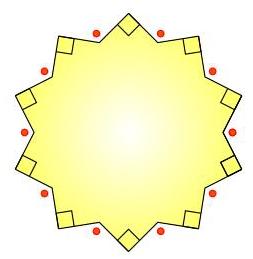
(A) 120° (B) 126° (C) 132°

(D) 138° (E) 142°

解法1

通过平分两个直角构造如图所示的四边形。由于该星形具有10阶旋转对称，直线\( {OA} \)是直线\( {OC} \)旋转\( {36}^{ \circ } \)所得，因此\( \angle {AOC} = {36}^{ \circ } \)。问题要求求出\( {x}^{ \circ } = \angle {ABC} \)。

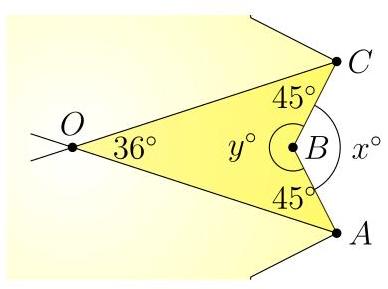
该四边形的内角和为\( {360}^{ \circ } \)，同时\( x + y = {360}^{ \circ } \)。于是\( x = {36} + {45} + {45} = {126}, \)，故选(B)。解法2

按图所示标记各点。由于10阶对称，当线段\( {AB} \)绕星形中心顺时针旋转\( {36}^{ \circ } \)时，它变为边\( {CD} \)。再将该线段绕\( C \)继续顺时针旋转\( {90}^{ \circ } \)，它变为边\( {CB} \)。

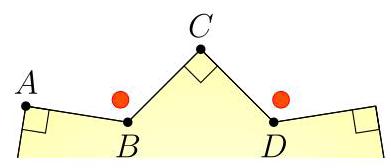
也就是说，\( {AB} \)可顺时针共旋转\( {126}^{ \circ } \)而变为\( {CB} \)。于是\( \angle {ABC} = {126}^{ \circ } \)，

故选(B)。

解法3

二十边形的内角和为\( \left( {{20} - 2}\right) \times {180}^{ \circ } = {3240}^{ \circ } \)。10个直角之和为\( {900}^{ \circ } \)，因此10个内部优角之和为\( {3240} - {900} = {2340}^{ \circ } \)，每个优角为\( {234}^{ \circ } \)。

标有圆点的角均为\( {360} - {234} = {126}^{ \circ } \)，

故选(B)。

解法4

如图所示作外接十边形。由于旋转对称，该十边形为正十边形，其内角为\( {144}^{ \circ } \)，且十个全等小三角形彼此全等。

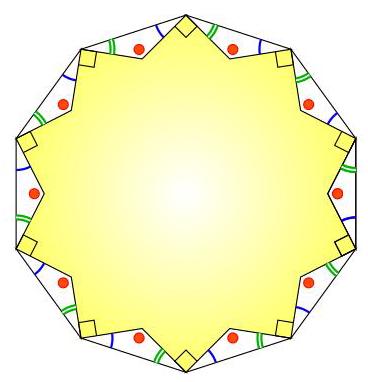
\[ {90}^{ \circ } + \bigtriangleup + \bigtriangleup = {144}^{ \circ } \]

\[ \Delta + \Delta = {54}^{ \circ } \]

\[ \cdot \cdot + \bigtriangleup + \bigtriangleup + \bigtriangleup = {180}^{ \circ } \]

\[ \text{-} = {180}^{ \circ } - {54}^{ \circ } = {126}^{ \circ } \]

故选(B)。

在这一顺序中，第42个数是多少？

(A) 15234 (B) 21354 (C) 23154 (D) 24531 (E) 24513 方法1 按顺序列出后，我们得到

\( \begin{array}{llll} {12345} & {13245} & {14235} & {15}\ldots \end{array} \) \( \begin{array}{lll} {12354} & {13254} & {14253} \end{array} \) \( \begin{array}{lll} {12435} & {13425} & {14325} \end{array} \) \( \begin{array}{lll} {12553} & {13452} & {14352} \end{array} \) \( \begin{array}{lll} {12543} & {13524} & {15234} \end{array} \) \( \begin{array}{lll} {12534} & {13542} & {15243} \end{array} \)

于是，我们看到它们以6个为一组，从12、13、14、15、21、22、23、24、25等开始。因此，第42个数将是该模式中第7组的最后一个，即以24开头的6个数中的最后一个，即24531，

故选(D)。

方法2

列表中共有\( 5! = {120} \)个数。其中\( 4! = {24} \)个以‘1’开头，接着24个以‘2’开头，依此类推。因此，列表中的第42个数是以‘2’开头的第21个数。

在以‘2’开头的24个数中，6个以‘21’开头，接着6个以‘23’开头，6个以‘24’开头。因此，所求的数是以‘24’开头的最后一个(最大)数。这就是24531，故选(D)。

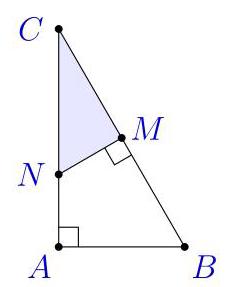
(A) \( \frac{1}{3} \) (B) \( \frac{1}{\sqrt{5}} \) (C) \( \frac{2}{5} \) (D) \( \frac{\sqrt{5}}{8} \) (E) \( \frac{5}{16} \)

方法1

选取单位使\( {AB} \)的长度为2。则\( {AC} = 4,{BC} = 2\sqrt{5} \)和

\( {CM} = {BM} = \sqrt{5} \)。由于在\( C \)处有公共角，在\( A \)和\( M,\bigtriangleup {CAB} \)处为直角，

与\( \bigtriangleup {CMN} \)相似，因此它们的面积比为\( {\left( \frac{CM}{CA}\right) }^{2} = {\left( \frac{\sqrt{5}}{4}\right) }^{2} = \frac{5}{16} \)，

故选(E)。

方法2

按图示在\( 2 \times 4 \)网格上绘制，使\( \bigtriangleup {ABC} \)的面积为4。

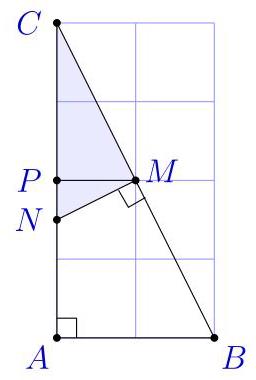
则\( \bigtriangleup {ABC} \)与\( \bigtriangleup {MNC} \)因两个公共角而相似。同理，\( \bigtriangleup {MNC} \)与\( \bigtriangleup {PNM} \)相似。于是\( {PN} = \frac{1}{2}{MP} = \frac{1}{2},{CN} = \frac{5}{2} \)，且\( \bigtriangleup {MNC} \)的面积为\( \frac{5}{4} \)，即\( \frac{5}{16} \)倍的\( \bigtriangleup {ABC} \)面积，故选(E)。

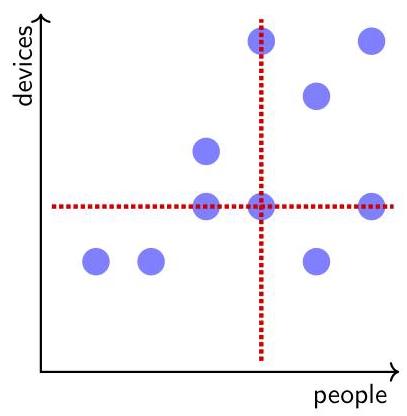
散点图展示了每户人家的人数及其联网设备数量。

为了对数据进行分类，她添加了一条垂直线表示人数的中位数(median number of people)，并添加了一条水平线表示设备数量的中位数(median number of devices)。

又调查了一户家庭，其结果被添加到散点图中。中位线会发生什么变化？

(A) 两条线都移动。(B) 两条线都不移动。

(C)只有垂直线移动。

(E) 这取决于新点的位置。

原始散点图上有10个数据点，因此垂直中位线穿过第5和第6个质量值的平均值。同样，水平中位线穿过第5和第6个长度值的平均值。恰好在这两项测量中，第5和第6个值都相等，所以每条中位线都穿过(至少)两个点，而不是位于两点之间。

当新增一个数据点时，总点数变为11个，因此新的中位线必须分别穿过第6个质量值和第6个长度值。新数据集中的第6个值将等于原始数据集中的第5个或第6个值，具体取决于新增数据点的位置。但由于这两个值相等，新增数据点的位置实际上无关紧要，两条中位线都无需移动。

因此选(B)。2024年澳大利亚数学竞赛第21–25题，每题5分

2024年2月有5个星期四。下一次2月有5个星期四是在哪一年？

(A) 2028 (B) 2044 (C) 2048 (D) 2052 (E) 2080

在平年，二月有28天，因此每周的每一天都会出现4次。只有在闰年，二月有29天时，才可能出现5个星期四，而且必须满足2月1日是星期四这一条件。

从2024年2月1日到2028年2月1日共\( {366} + {365} + {365} + {365} = {1461} \)天，即208周零5天，因此2028年2月1日是星期二。同理，本世纪任何连续的4年都是1461天，所以星期会向前推进5天。

要让闰年的2月1日落在星期四，需要7次每次5天的推进，因此这将在28年后，也就是2052年，

因此选(D)。

(A) 36 (B) 37 (C) 38 (D) 39 (E) 40

设第一间房游客人数为\( m \)，第二间房游客人数为\( n \)，换房者年龄为\( x \)。则两间房游客总年龄分别为\( {45m} \)和\( {20n} \)。一人换房后得到\( {45m} - x = {46}\left( {m - 1}\right) \)和\( {20n} + x = {21}\left( {n + 1}\right) \)。化简得\( {46} - x = m \)和\( x - {21} = n \)。由于\( n - m = 7 \)，可得\( x - {21} - \left( {{46} - x}\right) = 7 \)，且\( x = {37} \)，

故选(B)。

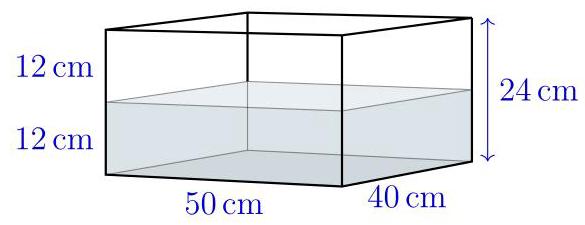
将边长为\( {20}\mathrm{\;{cm}} \)的实心立方体放入水箱，使其一面紧贴箱底。

水箱水位将上升多少？

(A) \( 3\mathrm{\;{cm}} \) (B) \( 4\mathrm{\;{cm}} \) (C) \( 5\mathrm{\;{cm}} \) (D) \( 8\mathrm{\;{cm}} \) (E) \( {12}\mathrm{\;{cm}} \)

计算取决于立方体是否完全浸没。为此，考虑立方体放入后水位升至立方体顶部时的体积，该体积为\( {50} \times {40} \times {20} - {20} \times {20} \times {20} = {40000} - {8000} = {32000}{\mathrm{\;{cm}}}^{3}. \)

而水箱中实际水量为\( {50} \times {40} \times {12} = {24000}{\mathrm{\;{cm}}}^{3} \)，仅达到立方体顶部所需体积的\( \frac{3}{4} \)。因此水位仅升至立方体高度的\( \frac{3}{4} \)，即\( {15}\mathrm{\;{cm}} \)。这比初始水位高\( 3\mathrm{\;{cm}} \)，

故选(A)。

谁周六完成的题数是周日的3倍？

(A) Amy (B) Bao (C) Cecil (D) Daria (E) Emilia

每位学生完成的题数取自集合

\( \{ {52},{53},{54},{55},{56},{57},{58},{59}\} \)且该集合中必须有六个不同元素。此外，对于每位学生，\( \# \)周六题量\( = k \times \# \)周日题量，因此\( \# \)周日题量\( + {\mathrm{k}}^{ * }\# \)周日题量\( = \left( {k = 1}\right) \times \# \)周日题量\( = \)总题量。这意味着\( k + 1 \)必须是\( \mathrm{k} = 1,2,3,4,5,6 \)完成总题量的一个因数。由于53和59是质数，它们没有\( > 1 \)和\( < 8 \)以外的因数，因此可以排除。由于56(Daria完成的题量)是列表中唯一能被7整除的数，Daria在周六完成的题量必须是周日的6倍。

同理，因为54(Bao完成的题量)和55(Cecil完成的题量)分别是唯一能被6和5整除的数，Bao和Cecil在周六完成的题量必须分别是周日的5倍和4倍。

在剩下的数中，52(Amy完成的题量)和57(Emilia完成的题量)分别是唯一能被4和3整除的数，因此Amy和Emilia在周六完成的题量必须分别是周日的3倍和2倍。

因此答案是Amy，即A。注意58(Felipe完成的题量)是剩下的唯一数，且能被2整除，所以Felipe在周六和周日完成的题量相同，

故选(A)。

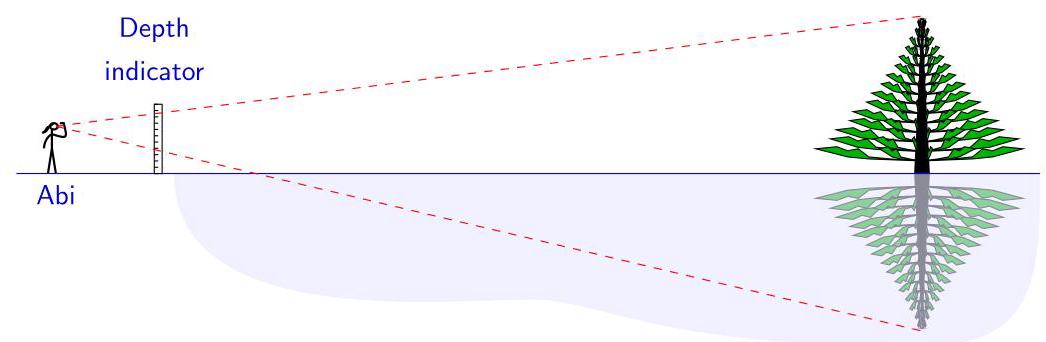
从Abi的视角看，树顶与深度指示器1.8米刻度对齐，而树顶的倒影与1.1米刻度对齐。Abi的眼睛高度与1.5米刻度齐平。树高多少米？

(A) 9 (B) 9.5 (C) 10 (D) 10.5 (E) 11

解法一

设\( x \)和\( y \)如图所示

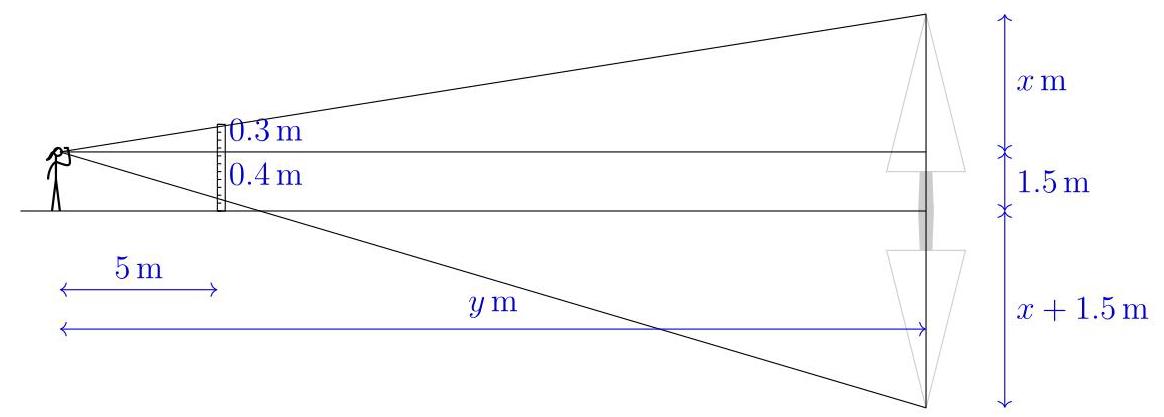
则\( \frac{x}{y} = \frac{0.3}{5} = {0.06} \)和\( \frac{x + 3}{y} = \frac{0.4}{5} = {0.08} \)。于是\( {0.08} - {0.06} = \frac{x + 3}{y} - \frac{x}{y} = \frac{3}{y} \)，因此\( y = \frac{3}{0.02} = {150} \)。于是\( x = {0.06y} = 9 \)，树高\( 9 + {1.5} = {10.5} \)米，故选(D)。

解法二

考虑Abi看向树基的视线。在深度指示器处，该视线穿过\( {1.1}\mathrm{\;m} \)和\( {1.8}\mathrm{\;m} \)刻度的中点，即\( {1.45}\mathrm{\;m} \)刻度。因此该视线每水平一米下降\( 1\mathrm{\;{cm}} \)。延伸到树处，视线已下降\( {150}\mathrm{\;{cm}} \)，所以树距Abi\( {150}\mathrm{\;m} \)。

从Abi眼睛到树顶的连线每水平一米上升\( {30} \div 5 = 6\mathrm{\;{cm}} \)。特别地，150米后该线已上升\( {150} \times {0.06} = 9 \)米。这意味着树顶在Abi眼高之上9米，因此树高10.5米

，

故选(D)。

方案3

这是阿比在刻度尺上看到的:\( A = \)树顶在1.1处的倒影，\( B = \)树基在\( {1.45}, C = \)与眼平齐的1.5处，\( D = \)树顶在1.8处。因此\( {BC} = {0.05} \)而实际树高是此处读数的30倍。树高为\( {30} \times {BD} = {30} \times {0.35} = {10.5} \)米，

故选(D)。第26-30题，请在答题卡指定区域将答案涂成0到999之间的整数。第26-30题分值依次为6、7、8、9、10分。26. 在所示的乘法谜题中，\( a, b \)和\( c \)代表不同数字。该谜题有两个不同解。问:形如abc的两个可能的三位数之差是多少？

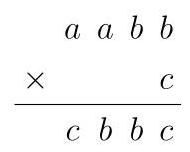
由乘积的千位数字\( c \)，我们得出\( a = 1 \)。

接着，将每个数用其各位数字表示为代数式，问题变为

\[ \left( {{1100} + {11b}}\right) \times c = {1001c} + {110b} \]

\[ {11bc} = - {99c} + {110b} \]

\[ {bc} = - {9c} + {10b} \]

\[ 0 = {bc} + {9c} - {10b} \]

\[ = \left( {b + 9}\right) \left( {c - {10}}\right) + {90} \]

\[ {90} = \left( {9 + b}\right) \left( {{10} - c}\right) \]

现在\( 1 \leq b, c \leq 9 \)，因此最后一行90的分解只能是\( {10} \times 9 \)、\( {15} \times 6 \)或\( {18} \times 5 \)之一。但第一种分解得到\( b = c = 1 \)，含有重复数字。故只有第二或第三种分解有效:要么\( b = 6 \)和\( c = 4 \)，要么\( b = 9 \)和\( c = 5 \)。验证后，\( {1166} \times 4 = {4664} \)和\( {1199} \times 5 = {5995} \)均为该谜题的解。

于是三位数abc有两个可能值，即164和195，因此\( {195} - {164} = {31} \)，故答案为(31)。

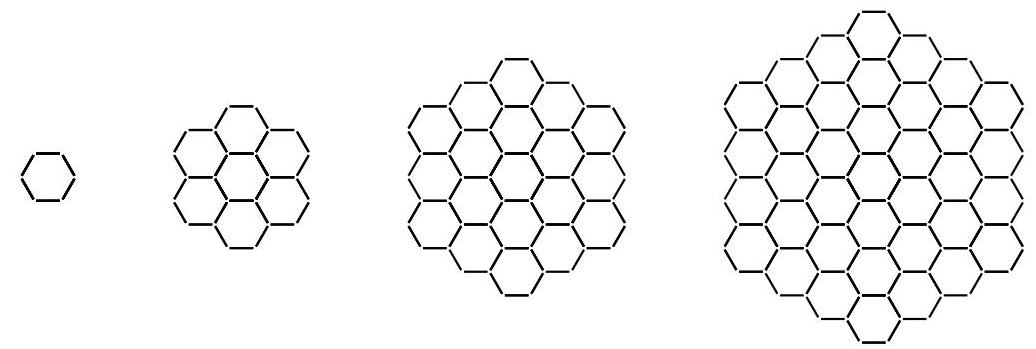
罗德尼从2000根杆开始，尽可能大地搭建一个这样的图形。他将剩下多少根杆？

方案1

假设图形每边有\( N \)个六边形。先考虑水平杆，按竖直列计数。这些列依次是

\[ \underset{N - 1}{\underbrace{\left( {N + 1}\right) + \left( {N + 2}\right) + \cdots + \left( {{2N} - 1}\right) }} + \left( {2N}\right) + \underset{N - 1}{\underbrace{\left( 2N - 1) + \cdots + \left( N + 1\right) \right) }} \]

我们将其重排，使每对和为\( {3N} \)，如\( \left( {N + 1}\right) + \left( {{2N} - 1}\right) = {3N} \)，

\( \left( {N + 2}\right) + \left( {{2N} - 2}\right) = {3N} \)等等，于是水平杆总数为

\[ \underset{N - 1}{\underbrace{{3N} + {3N} + \cdots + {3N}}} + \left( {2N}\right) = \left( {N - 1}\right) \left( {3N}\right) + {2N} = 3{N}^{2} - N \]

还有两个方向，但杆数相同，总杆数为\( 9{N}^{2} - {3N} \)。估算得\( {2000} \approx 9{N}^{2} - {3N} \approx 9{N}^{2} \)，因此\( N \approx \sqrt{{2000} \div 9} \approx \sqrt{225} = {15} \)。于是我们在15附近测试\( N \):

\( N \)	14	15	16
\( 9{N}^{2} - {3N} \)	1722	1980	2256

因此最大的\( N \)可以是15，然后还剩下\( {2000} - {1980} = {20} \)根杆，

因此(20)。方法二 在形状编号\( n \)中，设\( R \approx {2000} \)为杆的数量，\( H \)为六边形的数量。边界上有\( B = 6\left( {{2n} - 1}\right) = {12n} - 6 \)根杆，非边界杆有\( R - B \)根。每个六边形周围数6根杆会把每根边界杆数一次，每根非边界杆数两次。所以\( {6H} = B + 2\left( {R - B}\right) = {2R} - B = {2R} - {12n} + 6 \)，于是\( R = {3H} + {6n} - 3. \)

通过考虑六边形的同心层，

\[ H = 1 + 6 + {12} + \cdots + 6\left( {n - 1}\right) \]

\[ = 1 + 6 \times \left( {1 + 2 + \cdots + \left( {n - 1}\right) }\right) \]

\[ = 1 + 6 \times \frac{n\left( {n - 1}\right) }{2} \]

\[ = 3{n}^{2} - {3n} + 1 \]

\[ \Rightarrow R = {3H} + {6n} - 3 = 3\left( {3{n}^{2} - {3n} + 1}\right) + {6n} - 3 \]

\[ = 9{n}^{2} - {3n} \]

于是\( 9{n}^{2} - {3n} - R = 0 \)，其中\( R \leq {2000} \)。我们解这个关于\( n > 0 \)的二次方程:

\[ 9{n}^{2} - {3n} - R = 0 \]

\[ n = \frac{1}{18}\left( {3 + \sqrt{9 + {36R}}}\right) \]

\[ \leq \frac{1}{6} + \frac{1}{18}\sqrt{{36} \times {2025}} \]

\[ = \frac{1}{6} + \frac{6 \times {45}}{18} \]

\[ = {15} + \frac{1}{6} \]

这表明\( n = {15} \)是可能的。验证一下，当\( n = {15} \)时杆的数量为\( {3n}\left( {{3n} - 1}\right) = {45} \times {44} = {1980} \)根，这是可行的。下一个形状有\( n = {16} \)，需要\( {48} \times {47} > {45}^{2} = {2025} \)根杆，这太多了。

所以最大的形状每边有15个六边形。它需要1980根杆，还剩下\( {2000} - {1980} = {20} \)根杆，因此(20)。

\[ {xy} + x + y = {2024} \]

\[ {yz} + y + z = {2024} \]

\[ {zx} + z + x = {624}. \]

\( x + y + z \)的值是多少？方法一 在每个方程两边同时加1，使得

\[ \left( {x + 1}\right) \left( {y + 1}\right) = {2025} = {3}^{4}{5}^{2} \]

\[ \left( {y + 1}\right) \left( {z + 1}\right) = {2025} = {3}^{4}{5}^{2} \]

\[ \left( {z + 1}\right) \left( {x + 1}\right) = {625} = {5}^{4} \]

于是\( x + 1 = \frac{2025}{y + 1} = z + 1 \)，因此\( x = z \)。然后\( {\left( x + 1\right) }^{2} = {5}^{4} \)，因此\( x = {5}^{2} - 1 = {24} \)。最后\( y + 1 = \frac{{3}^{4}{5}^{2}}{{5}^{2}} = {81} \)，因此\( y = {80} \)且\( x + y + z = {24} + {80} + {24} = {128} \)，故(128)。方法二 由前两个方程，

\[ x = \frac{{2024} - y}{y + 1} = z \]

第三个方程与\( z = x \)为\( {x}^{2} + {2x} - {624} = 0 \)。利用二次方程，

\[ x = \frac{-2 \pm \sqrt{4 + 4 \times {624}}}{2} = - 1 \pm \sqrt{625} = - 1 \pm {25} \]

由于\( x > 0, x = z = {24} \)。于是第一个方程为\( {24y} + {24} + y = {2024} \)，因此\( y = {2000} \div {25} = {80} \)。然后\( x + y + z = {24} + {80} + {24} = {128} \)，故(128)。

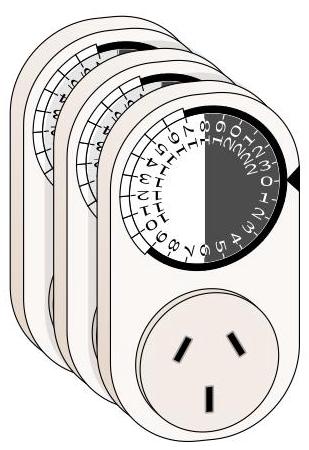
当表盘时间位于9:00到17:00之间时，定时器开关接通，于是插头上的电源被传递到插座。

为了好玩，他把三个定时器串联起来，全部设为0:00，并把一盏灯插在最前面的插座。灯多久后会亮起？

方法一

把定时器从前到后依次称为\( \mathrm{A},\mathrm{B},\mathrm{C} \)。

当计时器A已通电9小时、即将进入第10小时时，灯将亮起。

为此，计时器B将在第一次旋转中提供8小时，在第二次旋转中提供1小时。也就是说，它已完成一次旋转，并显示10:00。这意味着它已接收34小时电力，并即将开始第35小时。

为了让计时器C输出34小时电力，它需完成4次旋转(共32小时电力)并显示11:00。即，从首次通电起已过去4天11小时，如下图所示:

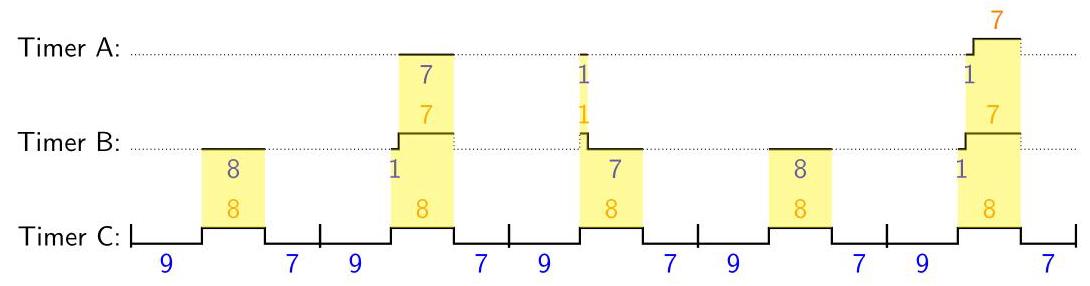
也就是说，107小时后，

因此(107)。

方案2

设\( y = f\left( x\right) \)表示\( y = \)计时器插座已通电的小时数，作为\( x = \)其插头通电小时数的函数。问题要求最大的\( x \)使得\( f\left( {f\left( {f\left( x\right) }\right) }\right) = 0 \)。

\( f \)的图像如图所示。

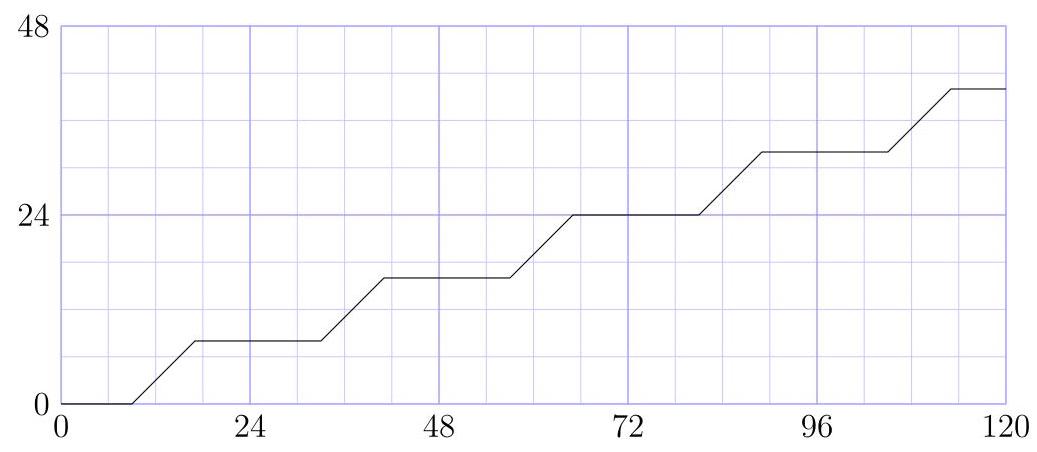
注意\( f\left( 9\right) = 0 \)和\( f\left( {9 + h}\right) = h \)对于\( 0 \leq h \leq 1 \)。

于是\( f\left( {33}\right) = 8 \)和\( f\left( {{33} + h}\right) = 8 + h \)对于\( 0 \leq h \leq 8 \)。因此\( f\left( {34}\right) = 9 \)和\( f\left( {{34} + h}\right) = 9 + h \)对于\( 0 \leq h \leq 1 \)。从而\( f\left( {f\left( {{34} + h}\right) }\right) = h \)对于\( 0 \leq h \leq 1 \)。

于是\( f\left( {105}\right) = {32} \)和\( f\left( {{105} + h}\right) = {32} + h \)对于\( 0 \leq h \leq 8 \)。因此\( f\left( {107}\right) = {34} \)和

\( f\left( {{107} + h}\right) = {34} + h \)对于\( 0 \leq h \leq 1 \)。从而\( f\left( {f\left( {f\left( {{107} + h}\right) }\right) }\right) = h \)对于\( 0 \leq h \leq 1 \)。

也就是说，灯在Tim打开开关后107小时内保持熄灭，随后亮起，

因此(107)。

求距离\( {CP} \)的平方？

方案1

由于\( {12}^{2} + {16}^{2} = {20}^{2} \)，三角形\( {ABC} \)在\( A \)处有一个直角。

假设该直线分别与三角形的边\( {AB} \)和\( {BC} \)交于点\( P \)和\( Q \)。若\( \left| {BP}\right| = a \)，则周长条件意味着\( \left| {BQ}\right| = {24} - a \)。面积条件进而推出

\[ \frac{\operatorname{area}\left( {\bigtriangleup {BPQ}}\right) }{\operatorname{area}\left( {\bigtriangleup {BAC}}\right) } = \frac{1}{2} \Rightarrow \frac{\frac{1}{2}\left| {BP}\right| \cdot \left| {BQ}\right| \cdot \sin \angle {PBQ}}{\frac{1}{2}\left| {BA}\right| \cdot \left| {BC}\right| \cdot \sin \angle {ABC}} = \frac{1}{2} \]

\[ \Rightarrow \;\frac{a \cdot \left( {{24} - a}\right) }{{12} \cdot {20}} = \frac{1}{2} \]

\[ \Rightarrow {a}^{2} - {24a} + {120} = 0 \]

\[ \Rightarrow \;a = \frac{{24} \pm \sqrt{9}}{2} = {12} \pm 2\sqrt{6}. \]

为使\( P \)和\( Q \)分别落在三角形的边\( {AB} \)和\( {BC} \)上，必须取解\( a = {12} - 2\sqrt{6} \)。(可以证明这是平面上唯一满足给定条件的直线。)由此得到\( \left| {BP}\right| = {12} - 2\sqrt{6} \)和\( \left| {AP}\right| = 2\sqrt{6} \)。

在三角形\( {CAP} \)中应用勾股定理(Pythagoras’s theorem)可得

\[ {\left| CP\right| }^{2} = {\left| CA\right| }^{2} + {\left| AP\right| }^{2} = {16}^{2} + {\left( 2\sqrt{6}\right) }^{2} = {280}. \]

故得(280)。

方案2

存在两种可能的构型，如图所示

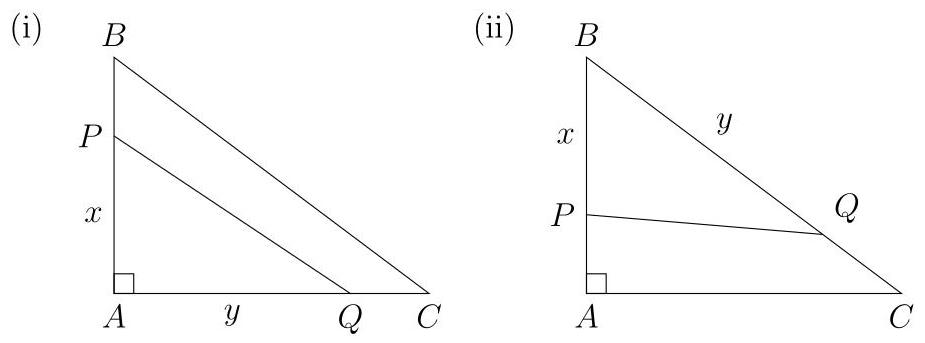
在情形(i)中，\( \bigtriangleup {APQ} \)是\( \bigtriangleup {ABC} \)面积的一半，因此

\[ \frac{xy}{2} = \frac{{16} \times {12}}{2} \Rightarrow {xy} = {96} \]

由于周长被平分，\( x + y = {24} \)。于是\( x\left( {{24} - x}\right) = {96} \)，得到

\( {x}^{2} - {24x} + {96} = 0 \)。配方后，\( {\left( x - {12}\right) }^{2} = {12}^{2} - {96} = {48} \)，从而\( x = {12} \pm \sqrt{48} \)。于是\( y = {12} \mp \sqrt{48} \)。然而\( {12} + \sqrt{48} > {18} \)，而\( x < {AB} = {12} \)且\( y < {AC} = {16} \)。因此情形(i)无解。

在情形(ii)中，\( \bigtriangleup {BPQ} \)与\( \bigtriangleup {BAC} \)的面积之比必须等于\( {xy} \)与\( {AB} \times {BC} = {12} \times {20} \)之比。由于该比值必须为\( \frac{1}{2} \)，我们有

\( {xy} = \frac{1}{2} \times {12} \times {20} = {120} \)。同样，\( x + y = {24} \)。于是\( x\left( {{24} - x}\right) = {120} \)，整理并配方得\( {\left( x - {12}\right) }^{2} = {24} \)。解得\( x = {12} \pm \sqrt{24} = {12} \pm 2\sqrt{6} \)。但\( x < {12} \)，因此\( x = {12} - 2\sqrt{6} \)，进而\( y = {12} + 2\sqrt{6} \)。验证得

\( y < {12} + 2 \times 3 = {18} < {20} = {BC}. \)

于是\( {\left( CP\right) }^{2} = {16}^{2} + {\left( {12} - x\right) }^{2} = {16}^{2} + {\left( 2\sqrt{6}\right) }^{2} = {256} + {24} = {280} \)，

故得(280)。