1.
When the expression \( \frac{\left( {{2}^{2} - 1}\right) \times \left( {{3}^{2} - 1}\right) \times \left( {{4}^{2} - 1}\right) \times \left( {{5}^{2} - 1}\right) }{\left( {2 \times 3}\right) \times \left( {3 \times 4}\right) \times \left( {4 \times 5}\right) \times \left( {5 \times 6}\right) } \) is simplified, which of the following is obtained?
下列哪项是表达式 \( \frac{\left( {{2}^{2} - 1}\right) \times \left( {{3}^{2} - 1}\right) \times \left( {{4}^{2} - 1}\right) \times \left( {{5}^{2} - 1}\right) }{\left( {2 \times 3}\right) \times \left( {3 \times 4}\right) \times \left( {4 \times 5}\right) \times \left( {5 \times 6}\right) } \) 化简后的结果?
A \( \frac{1}{2} \) B \( \frac{1}{3} \) C \( \frac{1}{4} \) D \( \frac{1}{5} \) E \( \frac{1}{6} \)
2.
What is the smallest prime which is the sum of five different primes?
有一个质数, 是五个不同质数之和, 请问这个质数最小是多少?
A 39 B 41 C 43 D 47 E 53
3.
The figure shows a regular hexagon.
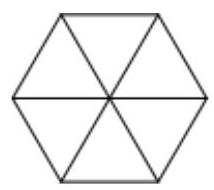
How many parallelograms are there in the figure?
如图所示是一个正六边形。请问图中有多少个平行四边形?
A 2 B 4 C 6 D 8
E more than 8 超过 8 个
4.
The diagram shows two symmetrically placed squares with sides of length 2 and 5 . What is the ratio of the area of the small square to that of the shaded region? 如图所示,边长分别为 2 和 5 的两个正方形对称叠放在一起。 请问小正方形与阴影部分的面积之比是多少?
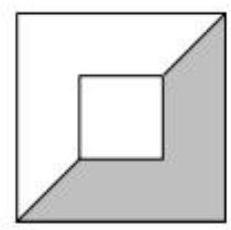
A7 : 24 B \( 1 : 3 \) C \( 8 : {25} \) D 8 : 21 E2 : 5
5.
What is the value of \( \frac{1}{1.01} + \frac{1}{1.1} + \frac{1}{1} + \frac{1}{11} + \frac{1}{101} \) ?
请问 \( \frac{1}{1.01} + \frac{1}{1.1} + \frac{1}{1} + \frac{1}{11} + \frac{1}{101} \) 的值是多少?
A 2.9 B 2.99 C 3 D 3.01 E 3.1
6.
What is the value of \( \frac{{4}^{800}}{{8}^{400}} \) ?
请问 \( \frac{{4}^{800}}{{8}^{400}} \) 的值是多少?
A \( \frac{1}{{2}^{400}} \) B \( \frac{1}{{2}^{200}} \) C 1 D \( {2}^{200} \) E \( {2}^{400} \)
7.
In 2021, a first class postage stamp cost 85p and a second class postage stamp cost 66p. In order to spend an exact number of pounds and to buy at least one of each type, what is the smallest total number of stamps that should be purchased?
2021 年, 一等邮票的价格为 85 便士, 二等邮票的价格为 66 便士。要想恰好花费整数英镑且每种邮票至少购买一张,请问最少需要购买多少张邮票? (1 英镑 = 100 便士)
A 10 B 8 C7 D 5 E 2 8. In the diagram, the outer hexagon is regular and has an area of 216. What is the shaded area? 如图所示,最外面的六边形是正六边形,面积为 216 。 请问阴影部分的面积是多少?
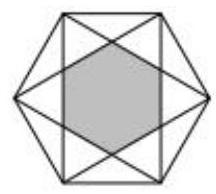
E 72
A 108 B 96 C 90 D 84
9.
A light-nanosecond is the distance that a photon can travel at the speed of light in one billionth of a second. The speed of light is \( 3 \times {10}^{8}{\mathrm{\;{ms}}}^{-1} \) .
How far is a light-nanosecond?
1 光纳秒是光子以光速在十亿分之一秒内传播的距离。光速为 \( 3 \times {10}^{8}{\mathrm{{ms}}}^{-1} \) .
请问 1 光纳秒有多远?
A \( 3\mathrm{\;{cm}} \) B \( {30}\mathrm{\;{cm}} \) C 3 m D \( {30}\mathrm{\;m} \) E \( {300}\mathrm{\;m} \)
10.
What is the value of \( x \) in the equation \( \frac{1 + {2x} + 3{x}^{2}}{3 + {2x} + {x}^{2}} = 3 \) ?
请问方程 \( \frac{1 + {2x} + 3{x}^{2}}{3 + {2x} + {x}^{2}} = 3 \) 中 \( x \) 的值是多少?
A -5 B -4 C-3 D -2 E -1
11.
In the number triangle shown, each disc is to be filled with a positive integer. Each disc in the top or middle row contains the number which is the product of the two numbers immediately below.
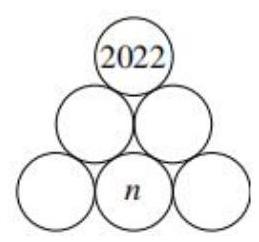
What is the value of \( n \) ?
图中数字三角形的每个圆圈内都要填入一个正整数。
顶行或中间行每个圆圈内的数字都是紧邻其下方的两个数字之积。 请问 \( n \) 的值是多少?
A 1 B 2 C 3 D 6 E 33
12.
What is the sum of the digits of the integer which is equal to \( {6666666}^{2} - {3333333}^{2} \) ?
\( {6666666}^{2} - {3333333}^{2} \) 的值是一个整数,请问这个整数的各个数位上的数字之和是多少?
A 27 B 36 C 45 D 54 E 63
13.
Three rugs have a combined area of \( {90}{\mathrm{\;m}}^{2} \) . When they are laid down to cover completely a floor of area \( {60}{\mathrm{\;m}}^{2} \) , the area which is covered by exactly two layers of rug is \( {12}{\mathrm{\;m}}^{2} \) .
What is the area of floor covered by exactly three layers of rug?
将三块总面积为 \( {90}{\mathrm{\;m}}^{2} \) 的地毯铺满面积为 \( {60}{\mathrm{\;m}}^{2} \) 的地面,
这时地面上恰好被两块地毯同时覆盖的面积为 \( {12}{\mathrm{\;m}}^{2} \) 。
请问地面上恰好被三块地毯同时覆盖的面积是多少?
\( \mathrm{A}2{\mathrm{\;m}}^{2} \) B \( 6{\mathrm{\;m}}^{2} \) C \( 9{\mathrm{\;m}}^{2} \) D \( {10}{\mathrm{\;m}}^{2} \) E \( {12}{\mathrm{\;m}}^{2} \)
14.
The diagram shows a square, \( {KLMN} \) . A second square \( {PQRS} \) is drawn inside it, as shown in the diagram, where \( P \) divides the side \( {KL} \) in the ratio \( 1 : 2 \) . Similarly, a third square \( {TUVW} \) is drawn inside \( {PQRS} \) with \( T \) dividing \( {PQ} \) in the ratio \( 1 : 2 \) .
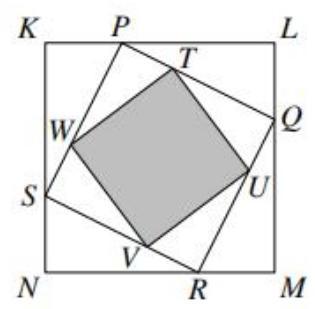
What fraction of the area of \( {KLMN} \) is shaded?
如图所示,在正方形 \( {KLMN} \) 内部再绘制第二个正方形 \( {PQRS} \) ,其中点 \( P \) 把边 \( {KL} \) 划分为 \( 1 : 2 \) 的两条线段。同样地,在 \( {PQRS} \) 内部再绘制第三个正方形 \( {TUVW} \) ,点 \( T \) 把边 \( {PQ} \) 划分为 \( 1 : 2 \) 的两条线段。请问正方形 \( {KLMN} \) 中阴影部分所占的比例是多少?
A \( \frac{25}{81} \) B \( \frac{16}{49} \) C \( \frac{4}{9} \) D \( \frac{40}{81} \) E \( \frac{2}{3} \)
15.
The hare and the tortoise had a race over \( {100}\mathrm{\;m} \) , in which both maintained constant speeds. When the hare reached the finish line, it was \( {75}\mathrm{\;m} \) in front of the tortoise. The hare immediately turned around and ran back towards the start line.
How far from the finish line did the hare and the tortoise meet?
兔子和乌龟进行了100米赛跑,期间它们都匀速奔跑。当兔子到达终点线时,乌龟还剩 75 米到达终点线。兔子立即转身向起跑线跑去。
请问当兔子和乌龟相遇时,它们离终点线有多少米?
A 54 B 60 C 64 D \( {66}\frac{2}{3} \) E 72
16.
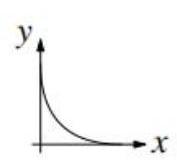
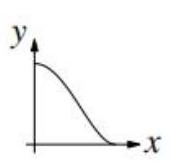
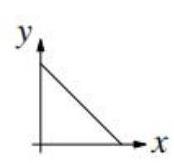
Which diagram could be a sketch of the curve \( \sqrt{x} + \sqrt{y} = 1 \) ?
下列哪张图是曲线 \( \sqrt{x} + \sqrt{y} = 1 \) 的图像?
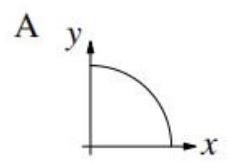
BC D E

17.
The shape shown is made by removing four equilateral triangles with side-length 1 from a regular octagon with side-length 1 .

What is the area of the shape?
右图中的图形是从边长为 1 的正八边形中去掉四个边长为 1 的等边三角形形成的。请问这个图形的面积是多少?
A \( 2 - 2\sqrt{2} + \sqrt{3} \) B \( 2 + 2\sqrt{2} - \sqrt{3} \) C \( 2 + 2\sqrt{2} + \sqrt{3} \)
D \( 3 - 2\sqrt{2} - \sqrt{3} \) E \( 2 - 2\sqrt{2} - \sqrt{3} \)
18.
The numbers \( x \) and \( y \) are such that \( {3}^{x} + {3}^{y + 1} = 5\sqrt{3} \) and \( {3}^{x + 1} + {3}^{y} = 3\sqrt{3} \) .
What is the value of \( {3}^{x} + {3}^{y} \) ?
数字 \( x \) 和 \( y \) 满足 \( {3}^{x} + {3}^{y + 1} = 5\sqrt{3},{3}^{x + 1} + {3}^{y} = 3\sqrt{3} \) 。
请问 \( {3}^{x} + {3}^{y} \) 的值是多少?
A \( \sqrt{3} \) B \( 2\sqrt{3} \) C 3 \( \sqrt{3} \) D \( 4\sqrt{3} \) E \( 5\sqrt{3} \)
19.
How many pairs of real numbers(x, y)satisfy the simultaneous equations \( {x}^{2} - y = {2022} \) and \( {y}^{2} - x = {2022}? \)
请问有多少个实数对(x, y)同时满足联立方程式 \( {x}^{2} - y = {2022} \) 和 \( {y}^{2} - x = {2022} \) ?
A infinitely many 无穷多 B 1 C 2 D 3 E 4 20. A square is inscribed inside a quadrant of a circle. The circle has radius 10 . What is the area of the square? 一个正方形内接于一个四分之一圆,圆的半径为 10。 请问这个正方形的面积是多少?
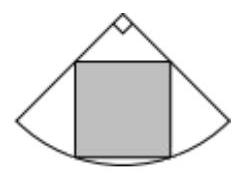
A 25 \( \sqrt{2} \) B 36 C \( {12\pi } \) D 40 E 30%
21.
The perimeter of a logo is created from two vertical straight edges, two small semicircles with horizontal diameters and two large semicircles. Both of the straight edges and the diameters of the small semicircles have length 2 . The logo has rotational symmetry as shown.

What is the shaded area?
一个标识的周长由两条垂直线段、两个直径水平的小半圆和两个
大半圆组成。两条垂直线段和两个小半圆的直径长度都为 2。
这个标识为旋转对称图形,如图所示。
请问阴影部分的面积是多少?
A 4 B \( 4 - \pi \) C 8 D \( 4 + \pi \) E 12
22.
How many pairs of integers(x, y)satisfy the equation \( \sqrt{x - \sqrt{x + {23}}} = 2\sqrt{2} - y \) ? 请问有多少个整数对(x, y)满足方程 \( \sqrt{x - \sqrt{x + {23}}} = 2\sqrt{2} - y \) ?
A 0 B 1 C 4 D 8
E infinitely many 无穷多
23.
Three squares \( {GQOP},{HJNO} \) and \( {RKMN} \) have vertices which sit on the sides of triangle \( {FIL} \) as shown. The squares have areas of 10,90 and 40 respectively.
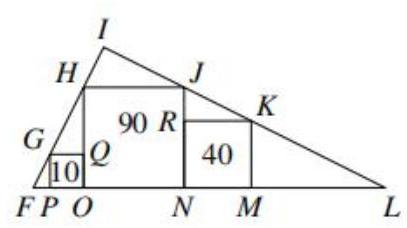
What is the area of triangle \( {FIL} \) ?
三个正方形 \( {GQOP},{HJNO} \) 和 \( {RKMN} \) 的一些顶点位于三角形 \( {FIL} \) 的边上, 如图所示。三个正方形的面积分别为 10、90 和 40。 请问三角形 \( {FIL} \) 的面积是多少?
A 220.5 B \( \frac{21}{5}\sqrt{10} \) C 252 D \( \frac{21}{2}\sqrt{10} \) E 441
24.
The numbers \( x, y, p \) and \( q \) are all integers. \( x \) and \( y \) are variable and \( p \) and \( q \) are constant and positive. The four integers are related by the equation \( {xy} = {px} + {qy} \) .
When \( y \) takes its maximum possible value, which expression is equal to \( y - x \) ?
数字 \( x\text{、}y\text{、}p \) 和 \( q \) 都是整数。其中 \( x \) 和 \( y \) 是变量, \( p \) 和 \( q \) 是常数且为正数。这四个整数满足方程 \( {xy} = {px} + {qy} \) 。当 \( y \) 取其最大可能值时,下面哪个表达式与 \( y - x \) 相等?
A \( {pq} - 1 \) \( \mathrm{B}\left( {p - 1}\right) \left( {q - 1}\right) \) C \( \left( {p + 1}\right) \left( {q - 1}\right) \) D \( \left( {p - 1}\right) \left( {q + 1}\right) \)
E \( \left( {p + 1}\right) \left( {q + 1}\right) \)
25.
A drinks carton is formed by arranging four congruent triangles as shown. \( {QP} = {RS} = 4\mathrm{\;{cm}} \) and \( {PR} = {PS} = {QR} = {QS} = {10}\mathrm{\;{cm}} \) .
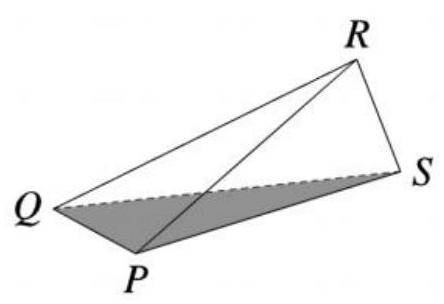
What is the volume, in \( {\mathrm{{cm}}}^{3} \) , of the carton?
一个饮料盒由四个全等三角形组成,如图所示。
\( {QP} = {RS} = 4\mathrm{\;{cm}},{PR} = {PS} = {QR} = {QS} = {10}\mathrm{\;{cm}} \) 。
请问这个饮料盒的体积是多少 \( {\mathrm{{cm}}}^{3} \) ?
A \( \frac{16}{3}\sqrt{23} \) B \( \frac{4}{3}\sqrt{2} \) C \( \frac{128}{25}\sqrt{6} \) D \( \frac{13}{2}\sqrt{23} \) E \( \frac{8}{3}\sqrt{6} \)














