解答
评注
这道题可以通过两次乘法计算 \( {2015}^{2} \) 和 \( {2016} \times {2014} \),再做一次减法来回答。显然,这种方法不可能是出题者的本意,因为它既繁琐又耗时。一定有更巧妙的方法。线索在于乘积 \( {2016} \times {2014} \) 可以改写为 \( \left( {{2015} + 1}\right) \times \left( {{2015} - 1}\right) \),而后一表达式恰好是平方差,即 \( {2015}^{2} - {1}^{2} \)。由此得到下面的解法。
[参见第22题,那里平方差分解同样发挥了作用。] 我们有
\[ {2015}^{2} - {2016} \times {2014} = {2015}^{2} - \left( {{2015} + 1}\right) \times \left( {{2015} - 1}\right) \]
\[ = {2015}^{2} - \left( {{2015}^{2} - 1}\right) \]
\[ = {2015}^{2} - {2015}^{2} + 1 \]
\[ = 1\text{.} \]
解答
我们有,
\[ {6x} = \frac{150}{x} \Leftrightarrow 6{x}^{2} = {150} \]
\[ \Leftrightarrow {x}^{2} = {25} \]
\[ \Leftrightarrow x = - 5\text{or}x = 5\text{.} \]
因此方程的两个解为 -5 和 5。于是所有解之和为 \( - 5 + 5 = 0 \)。
注意,这里的符号 \( \Leftrightarrow \) 表示“当且仅当”。
汽油价格在这段时间大约上涨了多少百分比? A 50% B 56% C 67% D 75% E \( {80}\% \)
SOLUTION
首先注意到 \( \pounds {40} \) 等于 \( {40} \times {100} \) 便士,即 4000 便士。因此路易丝拥有第一辆车时,汽油的单价(便士/升)为
\[ \frac{4000}{50} = {80} \]
同样地,前几天她加油时,汽油的单价(便士/升)为
\[ \frac{5000}{40} = {125} \]
于是汽油单价上涨了(125 - 80)便士/升,即 45 便士/升。相对于原价,这一涨幅的百分比为
\[ \frac{45}{80} \times {100} = \frac{4500}{80} \]
\[ = \frac{450}{8} \]
\[ = {56}\frac{1}{4}\text{.} \]
因此,在给定时期内汽油成本的增幅约为56%。
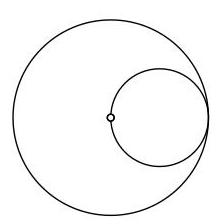
较大圆的面积中,有多少比例位于较小圆之外?
解答
由于较小的圆与较大的圆相切且穿过其圆心,因此较小圆的直径是较大圆直径的一半。由此可知,较小圆的半径是较大圆半径的一半。
半径为\( r \)的圆面积为\( \pi {r}^{2} \)。因此,半径为\( \frac{1}{2}r \)的圆面积为\( \pi {\left( \frac{1}{2}r\right) }^{2} = \frac{1}{4}\pi {r}^{2} \)。由此可知,较小圆的面积是较大圆面积的\( \frac{1}{4} \)。因此,较大圆面积的\( \frac{1}{4} \)位于较小圆内。故较大圆面积的\( \frac{3}{4} \)位于较小圆之外。
因为17、23和\( {2n} \)的平均数是\( n \),
\[ \frac{{17} + {23} + {2n}}{3} = n \]
因此,
\[ {17} + {23} + {2n} = {3n} \]
即,
\[ {40} + {2n} = {3n} \]
由此可得
\[ n = {40}\text{.} \]
因此,\( n \)的各位数字之和为\( 4 + 0 = 4 \)。
供探究
将数字5、6、7、8、9、10分别填入图中的六个圆圈,每个圆圈填一个数字,使得任意两个相邻圆圈中的数字之和为质数。已知数字5已填入最上方的圆圈。
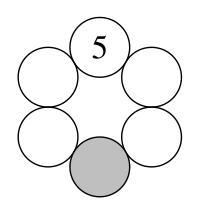
阴影圆圈里应填入哪个数字?
从5、6、7、8、9和10中任选两数相加得到的素数都大于2,因此必为奇素数。所以,若它们可表示为两整数之和,则其中必有一奇一偶。
因此,在任意一对相切的圆中,两个数必须一奇一偶。所以这些数在圆中的排列必须奇偶交替。因此,阴影圆中的数必须是偶数,即6、8或10。
由此我们还可推断,不在阴影圆内的偶数只能位于与顶部含数字5的圆相邻的那些圆中。
现在数字10不能与顶部圆圈相邻,因为\( 5 + {10} = {15} \)不是质数。因此,10必须是底部圆圈中的数字。
评论
在SMC(Senior Mathematical Challenge,高级数学挑战赛)的语境下,到此为止即可。若要给出完整解答,还需证明确实可以把数字6、7、8、9、10填入圆圈,使得每两个相邻圆圈中的数字之和均为素数。
为了完成解答,我们证明确实存在一种排列,使得数字10位于底部圆圈。容易验证,下面两幅图所示的排列均满足“每对相切圆中的数字之和为素数”的要求。注意,两图的唯一区别在于:左图中数字5、6、7、10、9、8按顺时针方向排列,而右图中则按逆时针方向排列。

供调查使用
解决方案
评论
这里最自然的方法是将每个分数化简为\( \frac{p}{q} \)的形式,其中\( p \)和\( q \)为正整数,然后观察这些化简后的分数中哪一个的值最大。
然而,如果你采用这种方法,你会发现只有一个分数大于1。
现在,当\( x \)和\( y \)为正数时,
\[ \frac{x}{y} > 1\text{ if, and only if }x > y\text{. } \]
因此,我们可以通过依次计算每个选项的分子\( x \)和分母\( y \)来回答这个问题,并证明只有一种情况下\( x > y \)成立。这样可以节省一些工作量。
在选项A中,分子\( \frac{1}{2} \)小于分母\( \frac{3}{4} \),因此该分数的值小于1。
在选项B中,分子为1,分母为
\[ \frac{\left( \frac{2}{3}\right) }{4} = \frac{2}{3} \times \frac{1}{4} = \frac{1}{6}. \]
由于分子大于分母,该分数的值大于1。在选项\( \mathrm{C} \)中,分子为
\[ \frac{\left( \frac{1}{2}\right) }{3} = \frac{1}{2} \times \frac{1}{3} = \frac{1}{6} \]
分母为4。由于分子小于分母,该分数的值小于1。
在选项D中,分子为1,分母为
\[ \frac{2}{\left( \frac{3}{4}\right) } = 2 \div \frac{3}{4} = 2 \times \frac{4}{3} = \frac{8}{3}. \]
由于分子小于分母,该分数的值小于1。最后,在选项E中,分子为
\[ \frac{1}{\left( \frac{2}{3}\right) } = 1 \div \frac{2}{3} = 1 \times \frac{3}{2} = \frac{3}{2} \]
分母为4。同样,分子小于分母,因此该分数的值也小于1。
因此,选项\( \mathrm{B} \)的值最大。
供探究
由1、2、3、4这四个数字构成的分数中,哪一个的值最大?
短语“as single digits”表示这些数字不能相邻放置,因此,例如,
\[ \frac{432}{1} \]
是不允许的。]
\[ \frac{\left( \frac{\left( \frac{1}{2}\right) }{\left( \frac{3}{4}\right) }\right) }{\left( \frac{\left( \frac{5}{6}\right) }{\left( \frac{7}{8}\right) }\right) } \]
将其写成\( \frac{p}{q} \)的形式,其中\( p \)和\( q \)为互质的正整数。
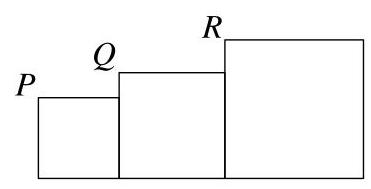
该图展示了八个小正方形。其中六个正方形需要被涂色,使得涂色的正方形构成一个立方体的展开图。
有多少种不同的方法可以做到这一点?
解决方案
评论
要回答这个问题,我们需要从给定图形中忽略两个方格,得到一系列网格,然后检查其中有多少种情况能构成正方体展开图(net of a cube)。图中共有28种不同的方式可以删去两个方格,数量相当可观!因此,我们首先要想办法减少需要检查的网格数量。
在检查网格时,在SMC(SMC)条件下,你可能需要运用视觉想象来判断它们是否能折叠成立方体。在SMC之外,你可以进行实际实验。
我们按照图中所示给方格编号。
我们首先指出,正方体的展开图不能同时使用正方形\( P \)和\( Q \),因为这两个正方形在折叠时必须构成同一个面。
每个展开图都包含正方形\( T \),否则它就不是一组连通的正方形。然而,没有任何一个立方体的展开图可以同时使用\( T, U, V \)和\( W \)这四个正方形。因此,每个展开图都必须舍弃\( U, V, W \)中的一个正方形。
因此,在不使用一对正方形的情况下,我们仅能得到立方体的六种展开图。这些展开图分别对应于不使用以下六对正方形:\( P \)、\( U, P \)、\( V, P \)、\( W, Q \)、\( U, Q \)、\( V, Q \)和\( W \)。依次忽略每一对正方形后得到的六个网格如下所示。

你应该能看出,这些图形都是立方体的展开图(net)。因此,用六个正方形组成立方体展开图共有六种不同的方式。
供探究
下列哪一个不可能是这样的交点数?
SOLUTION
下图各展示了四条直线在平纸上相交的情况,分别有1、3、4、5个交点。
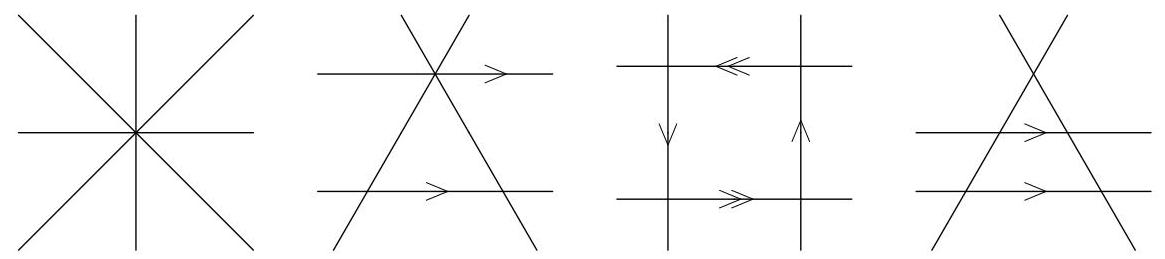
由此可知这些交点数是可能的,我们据此推断正确选项为B。
评注
在SMC(Senior Mathematical Challenge)中,当四个选项已被排除时,可安全地认定剩余选项正确。然而,为给出完整解答,我们需论证无法画出四条直线恰好产生两个交点。下面给出证明。
我们将证明:试图在平纸上画四条直线仅得两个交点注定失败。
假设我们欲画四条直线,仅产生两个交点,设这两点为\( P \)和\( Q \)。
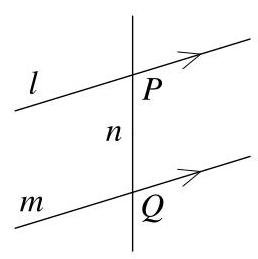
为使\( P \)成为交点,必须至少有两条直线经过\( P \)。因此除过\( P \)与\( Q \)的直线外,还需再画一条直线,记为\( l \),经过\( P \)。
同理,除过\( P \)与\( Q \)的直线外,还需再画一条直线,记为\( m \),经过\( Q \)。
直线\( l \)与\( m \)必须平行,否则将产生第三个交点。
此时可添加经过\( P \)与\( Q \)的直线,记为\( n \),而不会新增交点。然而,任何其他经过\( P \)的直线都不与\( m \)平行,从而将产生第三个交点,故无法画出。同理,也无法再画一条经过\( Q \)的直线而不产生第三个交点。
因此,在已画出直线\( l \)与\( m \)后,唯一可添加且不产生第三个交点的直线是\( n \)。于是无法画出四条直线恰好产生两个交点。供探究
解答
评注
在下面的解答中,我们使用求和公式
\[ 1 + 2 + \cdots + n = \frac{1}{2}n\left( {n + 1}\right) \]
用于计算从1到\( n \)的所有正整数之和。
如果你不熟悉这个公式,请参见下面的问题10.3和10.4。
因为Milly得到的总和与Billy相同,所以两人的总和都是1到20所有正整数之和的一半。我们可以把\( n = {20} \)代入公式\( \frac{1}{2}n\left( {n + 1}\right) \)得到这个总和。计算得\( \frac{1}{2} \times {20} \times {21} = {210} \)。因此Milly所加数字的总和是210的一半,即105。所以我们需要找到正整数\( n \)使得\( 1 + 2 + 3 + \cdots + n = {105} \)
方法1
我们依次尝试给出的每个选项,直到找到正确的\( n \)值。
为了检验选项A是否正确,需要判断从1到11的所有整数之和是否等于105。把\( n = {11} \)代入公式\( \frac{1}{2}n\left( {n + 1}\right) \),得到
\[ 1 + 2 + 3 + \cdots + {11} = \frac{1}{2} \times {11} \times {12} = {66}. \]
因此选项A不是正确答案。
我们接着依次检验其余选项。我们有
\[ 1 + 2 + \cdots + {12} = \left( {1 + 2 + \cdots + {11}}\right) + {12} = {66} + {12} = {78}. \]
\[ 1 + 2 + \cdots + {13} = \left( {1 + 2 + \cdots + {12}}\right) + {13} = {78} + {13} = {91}. \]
\[ 1 + 2 + \cdots + {14} = \left( {1 + 2 + \cdots + {13}}\right) + {14} = {91} + {14} = {105}. \]
因此\( n = {14} \)。所以选项\( \mathrm{D} \)正确。
在SMC的语境下,我们可以就此止步。
然而,一个完整的解答应当说明为何不存在其他满足条件的\( n \)值。见下文问题10.1。
方法二
为求最小的正整数\( n \),使得从1到\( n \)(含)的整数之和为105,我们解方程\( \frac{1}{2}n\left( {n + 1}\right) = {105} \)。我们有
\[ \frac{1}{2}n\left( {n + 1}\right) = {105} \Leftrightarrow n\left( {n + 1}\right) = {210} \]
\[ \Leftrightarrow {n}^{2} + n = {210} \]
\[ \Leftrightarrow {n}^{2} + n - {210} = 0 \]
\[ \Leftrightarrow \left( {n + {15}}\right) \left( {n - {14}}\right) = 0 \]
\[ \Leftrightarrow n = - {15}\text{or}n = {14}\text{.} \]
因为\( n \)是正整数,我们推断\( n = {14} \)。
注意,正如问题2的解答中那样,这里的符号\( \Leftrightarrow \)表示当且仅当。供探究
\[ \frac{1}{2}n\left( {n + 1}\right) = {105} \]
\[ \frac{1}{2}n\left( {n + 1}\right) = m \]
至多有一个正整数解。
...
记号\( {T}_{n} \)常用来表示第\( n \)个三角数,即
\[ {T}_{n} = 1 + 2 + 3 + \cdots + n. \]
在右侧图中,我们把两个对应和\( 1 + 2 + 3 + 4 + 5 + 6 \)的三角形点阵拼在一起,这两个三角形点阵共同构成一个6行7列的矩形,因此该矩形共有\( 6 \times 7 \)个点。于是该图说明\( 2{T}_{6} = 6 \times 7 \),从而\( {T}_{6} = \frac{1}{2}\left( {6 \times 7}\right) \)。

将上述做法推广,给出对所有正整数\( n \)的公式\( {T}_{n} = \frac{1}{2}n\left( {n + 1}\right) \)的证明。
我们从以下观察开始:
\[ {\left( k + 1\right) }^{2} - {k}^{2} = \left( {{k}^{2} + {2k} + 1}\right) - {k}^{2} = {2k} + 1. \]
因此,对\( k \)从1到\( n \)求和,我们得到
\[ \mathop{\sum }\limits_{{k = 1}}^{n}\left( {{\left( k + 1\right) }^{2} - {k}^{2}}\right) = \mathop{\sum }\limits_{{k = 1}}^{n}\left( {{2k} + 1}\right) \]
\[ = 2\mathop{\sum }\limits_{{k = 1}}^{n}k + \mathop{\sum }\limits_{{k = 1}}^{n}1\text{. } \]
即,
\[ \mathop{\sum }\limits_{{k = 1}}^{n}\left( {{\left( k + 1\right) }^{2} - {k}^{2}}\right) = 2{T}_{n} + n \]
说明上述方程左侧如何化简,然后整理方程以得到\( {T}_{n} \)的公式。
证明:若\( m = a, n = b \)是方程\( {T}_{m} = \frac{1}{2}{T}_{n} \)的解,则\( m = {3a} + {2b} + 2 \)和\( n = {4a} + {3b} + 3 \)也是解。
推得方程\( {T}_{m} = \frac{1}{2}{T}_{n} \)有无穷多个正整数解。[注意,这也可表述为:存在无穷多个正整数\( T \),使得\( T \)和\( {2T} \)均为三角数。]
他能搭出多少种不同高度的塔?
解答
评注
最直接的方法是列出所有选取三块积木的可能方式。为给出完整解答,需以系统方式列出,确保所有可能情况均出现且无一重复。下表按此原则编排,希望能让读者清楚我们已做到这一点。
下表列出所有边长为\( 4\mathrm{\;{cm}},6\mathrm{\;{cm}} \)或\( {10}\mathrm{\;{cm}} \)的三块积木组合,最后一列为对应塔的高度。
| 4厘米积木的数量 | 6厘米积木的数量 | 10厘米积木的数量 | 塔的高度 |
| 3 | 0 | 0 | 12厘米 |
| 0 | 3 | 0 | 18厘米 |
| 0 | 0 | 3 | 30厘米 |
| 2 | 1 | 0 | 14厘米 |
| 2 | 0 | 1 | 18厘米 |
| 1 | 2 | 0 | 16厘米 |
| 0 | 2 | 1 | \( {22}\mathrm{\;{cm}} \) |
| 1 | 0 | 2 | 24厘米 |
| 0 | 1 | 2 | 26厘米 |
| 1 | 1 | 1 | 20厘米 |
我们看到,拉希德可以用三种积木搭小塔,共有十种选择方式。然而,其中有两种搭出的塔高度相同,即\( {18}\mathrm{\;{cm}} \)。因此,拉希德能搭出9种不同高度的塔。
供探究
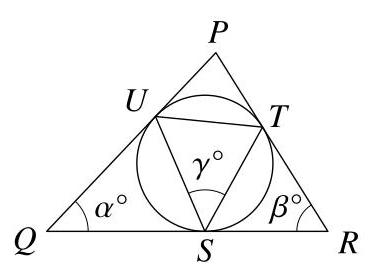
下列哪一项用\( \alpha \)和\( \beta \)表示\( \gamma \)?
解答
方法1
由已知圆与三角形各边相切,可推出直线\( {PQ},{QR} \)和\( {RP} \)均为圆的切线。从同一点到圆的两条切线长度相等。特别地,\( {QS} = {QU} \)。因此三角形\( {QSU} \)为等腰三角形,从而\( \angle {QSU} = \angle {QUS} \)。
由于三角形内角和为\( {180}^{ \circ } \),从三角形\( {QSU} \)可推出\( {\alpha }^{ \circ } + \angle {QSU} + \angle {QUS} = {180}^{ \circ } \)。
因为\( \angle {QSU} = \angle {QUS} \),所以\( {\alpha }^{ \circ } + 2\angle {QSU} = {180}^{ \circ } \)。可将此式整理为
\[ \angle {QSU} = \frac{1}{2}{\left( {180} - \alpha \right) }^{ \circ }. \]
同理,切线\( {RS} \)和\( {RT} \)长度相等。因此三角形\( {RTS} \)为等腰三角形,从而
\[ \angle {RST} = \frac{1}{2}{\left( {180} - \beta \right) }^{ \circ }. \]
由于\( {QSR} \)为一条直线,该直线上\( S \)处的角之和为\( {180}^{ \circ } \),即
\[ \angle {QSU} + \angle {RST} + {\gamma }^{ \circ } = {180}^{ \circ }. \]
将已求得的\( \angle {QSU} \)和\( \angle {RST} \)的表达式代入此式,可推出
\[ \frac{1}{2}{\left( {180} - \alpha \right) }^{ \circ } + \frac{1}{2}{\left( {180} - \beta \right) }^{ \circ } + {\gamma }^{ \circ } = {180}^{ \circ }. \]
可将此式整理为
\[ {180}^{ \circ } - \frac{1}{2}{\left( \alpha + \beta \right) }^{ \circ } + {\gamma }^{ \circ } = {180}^{ \circ }\text{,} \]
由此可得
\[ \gamma = \frac{1}{2}\left( {\alpha + \beta }\right) . \]
方法二
与方法一相同,\( {PQ} \) 和 \( {PT} \) 均为圆的切线。
根据交错角定理(Alternate Angle Theorem),\( \angle {PUT} = \angle {PTU} = {\gamma }^{ \circ } \)。因此,由于三角形 \( {PUT} \) 的内角和为 \( {180}^{ \circ } \),我们得到 \( \angle {UPT} + {\gamma }^{ \circ } + {\gamma }^{ \circ } = {180}^{ \circ } \),从而
\[ \angle {UPT} = {180}^{ \circ } - 2{\gamma }^{ \circ }. \]
因此,由于三角形 \( {PQR} \) 的内角和为 \( {180}^{ \circ } \),
\[ {\alpha }^{ \circ } + {\beta }^{ \circ } + \left( {{180}^{ \circ } - 2{\gamma }^{ \circ }}\right) = {180}^{ \circ }\text{.} \]
我们可以重新整理上述最后一个方程,得到
\[ 2{\gamma }^{ \circ } = {\alpha }^{ \circ } + {\beta }^{ \circ }, \]
于是可得
\[ \gamma = \frac{1}{2}\left( {\alpha + \beta }\right) . \]
供探究
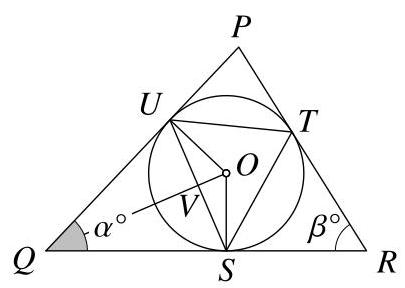
设 \( O \) 为圆心。在图中,我们添加了连接 \( O \) 与点 \( Q, S \) 和 \( U \) 的线段。令 \( V \) 为 \( {QO} \) 与 \( {US} \) 的交点。
现在按如下步骤进行。
(i) 证明三角形 \( {QOS} \) 与 \( {QOU} \) 全等。
(ii) 推导出 \( \angle {VQS} = \angle {VQU} = \frac{1}{2}{\alpha }^{ \circ } \)。
(iii) 证明三角形 \( {QVS} \) 与 \( {QVU} \) 全等。
(iv)推导出\( \angle {QVS} = {90}^{ \circ } \)。
(v)推导出\( \angle {USO} = \frac{1}{2}{\alpha }^{ \circ } \)。
(vi)同样地,证明\( \angle {TSO} = \frac{1}{2}{\beta }^{ \circ } \)。
(vii)得出结论\( \gamma = \frac{1}{2}\left( {\alpha + \beta }\right) \)。
SOLUTION
当其中一位杰克说“昨天我说谎了”时,这一天要么是他讲真话而前一天说谎,要么是他撒谎而前一天讲真话。
因此,对红桃杰克来说,那一天必须是星期一或星期五;同样,对方块杰克来说,那一天必须是星期五或星期二。
因此,他们都说“昨天我说谎了”的那一天是星期五。
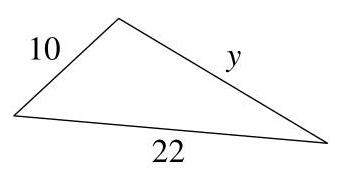
\( y \)的值是多少?
解法一
我们按图中所示给三角形的顶点标号。设\( N \)为从\( P \)到\( {QR} \)的垂线与\( {QR} \)的交点,并设\( h \)为\( {PN} \)的长度。
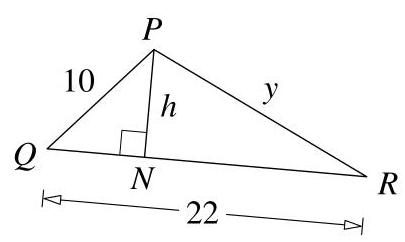
该三角形面积为88,因此根据三角形面积公式面积=\( = \)\( \frac{1}{2} \)(底×高),我们有
\[ {88} = \frac{1}{2}\left( {{22} \times h}\right) , \]
即\( {88} = {11h} \)。于是\( h = 8 \)。
对直角三角形\( {QNP} \)应用毕达哥拉斯定理(Pythagoras’ Theorem),我们有\( Q{N}^{2} + {h}^{2} = {10}^{2} \)。因此\( Q{N}^{2} = {10}^{2} - {h}^{2} = {10}^{2} - {8}^{2} = {100} - {64} = {36} \)。由于\( {QN} \)是长度,故为正,我们推断\( {QN} = 6 \)。[或者,你也可以直接注意到\( {PQN} \)是一个直角三角形,其边长比例为\( 5 : 4 : 3 \)。]
于是\( {NR} = {QR} - {QN} = {22} - 6 = {16} \)。现在,对直角三角形\( {PNR} \)应用毕达哥拉斯定理,我们有\( N{R}^{2} + {h}^{2} = {y}^{2} \),即\( {16}^{2} + {8}^{2} = {y}^{2} \)。因此\( {y}^{2} = {256} + {64} = {320} \)。我们推断\( y = \sqrt{320} = \sqrt{{64} \times 5} = 8\sqrt{5} \)。
METHOD 2
我们利用三角形面积公式\( \frac{1}{2}{ab}\sin \theta \),其中\( a \)和\( b \)为两条边的长度,\( \theta \)为这两边夹角,并结合余弦定理(Cosine Rule)。
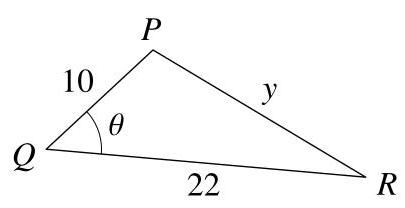
我们按图中所示给三角形顶点标号,并设\( \angle {PQR} = \theta \)。于是\( {88} = \frac{1}{2}\left( {{22} \times {10}}\right) \sin \theta \)。即\( {88} = {110}\sin \theta \)。因此
\[ \sin \theta = \frac{88}{110} = \frac{4}{5}. \]
由恒等式\( {\cos }^{2}\theta + {\sin }^{2}\theta = 1 \),可得
\[ {\cos }^{2}\theta = 1 - {\sin }^{2}\theta = 1 - {\left( \frac{4}{5}\right) }^{2} = 1 - \frac{16}{25} = \frac{9}{25} = {\left( \frac{3}{5}\right) }^{2}, \]
因此\( \cos \theta = \pm \frac{3}{5} \)。
由题图可知,\( \angle {PQR} \)为锐角,即\( 0 < \theta < {90}^{ \circ } \)。因此\( \cos \theta > 0 \),于是\( \cos \theta = \frac{3}{5} \)。
我们现在可以利用余弦定理推断
\[ {y}^{2} = P{Q}^{2} + Q{R}^{2} - {2PQ} \cdot {QR}\cos \theta \]
\[ = {10}^{2} + {22}^{2} - 2 \times {10} \times {22}\cos \theta \]
\[ = {100} + {484} - 2 \times {10} \times {22} \times \frac{3}{5} \]
\[ = {100} + {484} - {264} \]
\[ = {320}\text{.} \]
因此\( y = \sqrt{320} = 8\sqrt{5} \)。
评注
在下面的问题中,我们介绍回答第14题的第三种方法。该方法使用海伦公式(Heron's Formula)求三角形面积。
在方法1中,我们使用了以三角形高表示面积的公式。在方法2中,我们使用了涉及两边夹角的公式。海伦公式的优势在于,它仅根据三角形的三边长度即可给出面积。然而,如果你尝试下面的问题,就会发现该方法涉及相当复杂的代数运算。
海伦公式:边长分别为\( a, b \)和\( c \)的三角形,其面积\( A \)为
\[ A = \frac{1}{4}\sqrt{\left( {a + b + c}\right) \left( {-a + b + c}\right) \left( {a - b + c}\right) \left( {a + b - c}\right) }. \]
该公式也可写作
\[ A = \sqrt{s\left( {s - a}\right) \left( {s - b}\right) \left( {s - c}\right) }, \]
其中\( s = \frac{1}{2}\left( {a + b + c}\right) \)为三角形周长的一半。
供探究
亚历山大的海伦(Heron of Alexandria)生活在公元一世纪,是著名的几何学家和力学著作作者。他发明了包括蒸汽轮机在内的许多机械。他在其著作《度量学》(Metrica)中给出了三角形面积公式的证明。
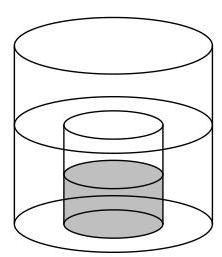
大花瓶中水的初始深度是多少?
解答
我们使用公式\( V = \pi {r}^{2}h \)计算半径为\( r \)、高度为\( h \)的圆柱体体积\( V \)。用圆柱体直径\( d \)表示,其中\( r = \frac{1}{2}d \),则公式变为\( V = \frac{1}{4}\pi {d}^{2}h \)。
当小花瓶完全压到底且水停止溢出后,大花瓶中的水位升至小花瓶顶部,因此水深等于小花瓶的高度,即\( {16}\mathrm{\;{cm}} \)。
于是大花瓶中水的体积等于直径为\( {20}\mathrm{\;{cm}} \)、高度为\( {16}\mathrm{\;{cm}} \)的圆柱体体积减去小花瓶空出的一半体积。
直径为\( {20}\mathrm{\;{cm}} \)、高度为\( {16}\mathrm{\;{cm}} \)的圆柱体体积为\( \frac{1}{4}\pi \times {20}^{2} \times {16}{\mathrm{\;{cm}}}^{3} = \)\( {1600\pi }{\mathrm{{cm}}}^{3} \)。小花瓶空出的一半体积为\( \frac{1}{4}\pi \times {10}^{2} \times 8{\mathrm{\;{cm}}}^{3} = {200\pi }{\mathrm{{cm}}}^{3} \)。
因此圆柱体中水的体积为,以\( {\mathrm{{cm}}}^{3} \)计,
\[ {1600\pi } - {200\pi } = {1400\pi }. \]
现设圆柱体中水的初始深度为\( x\mathrm{\;{cm}} \)。则圆柱体中水的体积为,以\( {\mathrm{{cm}}}^{3} \)计,
\[ \frac{1}{4}\pi \times {20}^{2} \times x = {100\pi x}. \]
由于这两个表示水体积的表达式必须相等,
\[ {100\pi x} = {1400\pi }, \]
由此可得\( x = {14} \)。
因此,圆柱中水的原始深度为\( {14}\mathrm{\;{cm}} \)。
从左到右排列它们有多少种方式?A 12 B 24 C 60 D 120 E 720 解答
我们设R2、R3、R4分别为拥有2、3、4个头的红色Fnargs(芬纳格斯),B2、B3、B4分别为拥有2、3、4个头的蓝色Fnargs(芬纳格斯)。我们需要计算将R2、\( \mathrm{R}3,\mathrm{R}4,\mathrm{\;B}2,\mathrm{\;B}3,\mathrm{\;B}4 \)排成一列的方式数,使得任意相邻的两只Fnargs(芬纳格斯)既不同色,也不同头数。
假设这一排六个Fnargs的最左端是R2。第二个Fnarg必须是蓝色且拥有3或4个头。因此,这一排要么以R2, B3开头,要么以R2, B4开头。
如果这一行以R2、B3开头,那么第三个Fnarg必须是红色且不能拥有3个头。由于R2已排在队中,第三个Fnarg只能是R4。第四个Fnarg必须是蓝色且不能拥有4个头。由于B3已在行内,这第四个Fnarg只能是B2。于是只剩下R3和B4需要放置。由于颜色必须交替,这一行中的第五和第六个Fnarg从左到右依次必须是R3和B4。因此,最终排列必须是
\( \mathrm{R}2,\mathrm{\;B}3,\mathrm{R}4,\mathrm{\;B}2,\mathrm{R}3,\mathrm{\;B}4 \) .
类似的论证表明,如果这一行以R2、B4开头,那么排列必须如上所述,但需将3和4互换,即
\( \mathrm{R}2,\mathrm{\;B}4,\mathrm{R}3,\mathrm{\;B}2,\mathrm{R}4,\mathrm{\;B}3 \) .
因此,只有两种方法可以完成以R2开头的行。
类似的论证表明,无论哪个Fnarg(弗纳格)开始一行,都只有两种方式可以完成该行。
由于这一行可以以六种Fnargs(芬纳格斯)中的任意一种开头,因此将它们排成一列的总方式数为\( 6 \times 2 = {12} \)。
供调查
该图展示了八个大小不同的圆。这些圆以同心圆对的形式排列,圆心构成一个正方形。每个较大的圆与另一个较大的圆以及两个较小的圆相切。较大圆的半径为1。
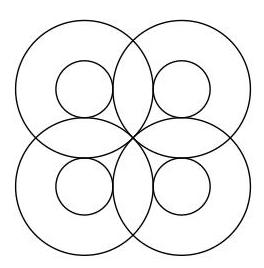
每个较小圆的半径是多少?
解答
设圆心分别为\( P, Q, R \)和\( S \),如图所示。设较小圆的半径为\( r \)。
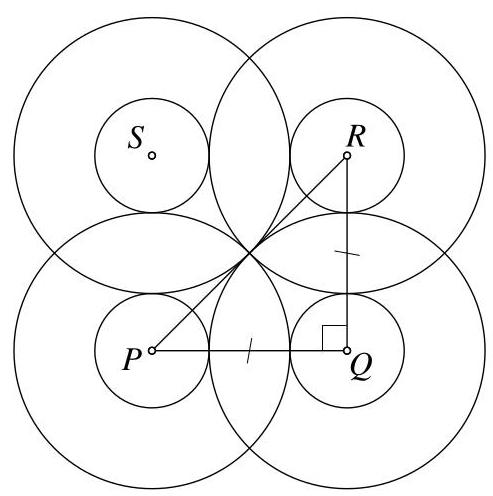
于是\( {PQ} \)的长度等于大圆半径与小圆半径之和,即\( {PQ} = 1 + r \)。同理\( {QR} = 1 + r \)。此外,\( {PR} \)是两个大圆半径之和,即\( {PR} = 1 + 1 = 2 \)。
因为\( {PQRS} \)是正方形,所以\( \angle {PQR} \)是直角。
因此,对三角形\( {PQR} \)应用勾股定理,我们有
\[ {\left( 1 + r\right) }^{2} + {\left( 1 + r\right) }^{2} = {2}^{2}\text{.} \]
于是
\[ 2{\left( 1 + r\right) }^{2} = 4 \]
从而
\[ {\left( 1 + r\right) }^{2} = 2 \]
因此
\[ 1 + r = \pm \sqrt{2} \]
从而
\[ r = \pm \sqrt{2} - 1 \]
由于半径必须为正,我们得出每个较小圆的半径为
\[ \sqrt{2} - 1 \]
评注
回答此题最直接的方法是首先计算10!,然后从最大的选项开始,依次检验其平方是否为10!的因数,直到找到满足条件的平方。
若进行乘法运算,你会发现\( {10}! = {3628800} \)。接着检验选项,你会发现\( {5040}^{2} \)不是10!的因数,而\( {720}^{2} \)是。
然而,这种方法存在若干缺点。在SMC中不允许使用计算器,而此方法需要大量计算。在SMC之外,我们也不只有五个选项可检验。我们必须从最大的整数\( k \)开始,使得\( {k}^{2} \leq {10} \)!,并检验\( {k}^{2} \)是否为10!的因数。若不是,则需检验\( {\left( k - 1\right) }^{2} \)是否为10!的因数,依此类推,直到找到平方为10!因数的最大整数。此外,该方法对问题本身缺乏洞察,若将10替换为更大的数,则此方法将不可行。
更好的方法是利用10!的质因数分解,基于“平方数的质因数分解中每个质数的指数均为偶数”这一事实。因此,我们首先将10!分解为质因数,然后在这些质因数中找出由偶次幂构成的最大乘积,该乘积即为10!的一个因数。
我们将10!表示为质数的乘积如下。
\[ {10}! = {10} \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \]
\[ = \left( {2 \times 5}\right) \times {3}^{2} \times {2}^{3} \times 7 \times \left( {2 \times 3}\right) \times 5 \times {2}^{2} \times 3 \times 2 \]
\[ = {2}^{8} \times {3}^{4} \times {5}^{2} \times 7 \]
\[ = {\left( {2}^{4} \times {3}^{2} \times 5\right) }^{2} \times 7\text{.} \]
我们推断\( {2}^{4} \times {3}^{2} \times 5 \)的平方是10!的因数,但不存在更大的整数\( k \)使得\( {k}^{2} \)是10!的因数。因此,最大的整数\( k \),其平方\( {k}^{2} \)是10!的因数,是\( {2}^{4} \times {3}^{2} \times 5 = {16} \times 9 \times 5 = {720}. \)。
供探究
它们分别是下列哪一组?
SOLUTION
我们设\( S, T, U \)和\( V \)为图中所示的点。
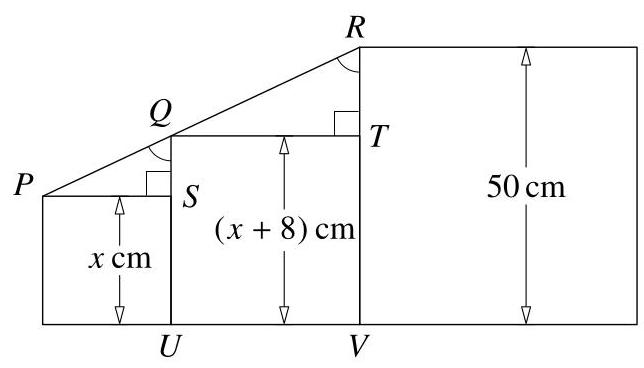
我们设最小正方形的边长为\( x\mathrm{\;{cm}} \)。
由此可知,中间正方形的边长为\( \left( {x + 8}\right) \mathrm{{cm}} \)
由于直线\( {QU} \)和\( {RV} \)均垂直于\( {UV} \),因此它们平行。于是,\( {PQR} \)为一条直线,对应角\( \angle {PQS} \)和\( \angle {QRT} \)相等。
由于图形由正方形构成,\( \angle {PSU} = \angle {QTV} = {90}^{ \circ } \)。因此,同一直线上的角之和为\( {180}^{ \circ } \),我们有\( \angle {PSQ} = \angle {QTR} = {90}^{ \circ } \)。于是,直角三角形\( {PSQ} \)和\( {QTR} \)因对应角相等而相似。因此
\[ \frac{QS}{PS} = \frac{RT}{QT} \]
现在\( {QS} \)的长度为\( 8\mathrm{\;{cm}},{PS} \),\( x\mathrm{\;{cm}},{RT} \)的长度为\( \left( {{50} - \left( {x + 8}\right) }\right) \mathrm{{cm}} = \left( {{42} - x}\right) \mathrm{{cm}} \),\( {QT} \)的长度为\( \left( {x + 8}\right) \mathrm{{cm}} \)。于是
\[ \frac{8}{x} = \frac{{42} - x}{x + 8} \]
将该方程两边同乘以\( x\left( {x + 8}\right) \),可见最后一个方程等价于
\[ 8\left( {x + 8}\right) = x\left( {{42} - x}\right) , \]
即
\[ {8x} + {64} = {42x} - {x}^{2}. \]
最后一个方程可整理为
\[ {x}^{2} - {34x} + {64} = 0. \]
现在可将该方程中的二次式因式分解为
\[ \left( {x - {32}}\right) \left( {x - 2}\right) = 0. \]
因此
\[ x = 2\text{or}x = {32}\text{.} \]
我们推断,最小正方形的边长可能为2和32(单位:\( \mathrm{{cm}} \))。
问:纸上被染黑的面积是多少(单位:\( {\mathrm{{cm}}}^{2} \))?
设\( O \)为正方形旋转时所绕的角。正方形的初始位置用实线表示,最终位置用虚线表示,于是最初位于\( P \)的角旋转至\( Q \)。
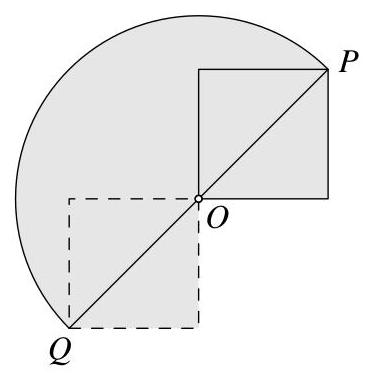
旋转过程中与纸面接触的区域已用阴影标出,这就是被染黑的部分。它由直径为\( {PQ} \)的半圆以及该半圆外两个阴影半正方形组成。
正方形边长为1(单位:\( \mathrm{{cm}} \))。设\( {OP} \)的长度为\( x\mathrm{\;{cm}} \),则由勾股定理得\( {x}^{2} = {1}^{2} + {1}^{2} = 2 \)。因此,直径为\( {PQ} \)的半圆面积为(单位:\( {\mathrm{{cm}}}^{2},\frac{1}{2}\pi {x}^{2} = \frac{1}{2}\pi \times 2 = \pi \))。
半圆外两个半正方形的面积等于一个边长为\( 1\mathrm{\;{cm}} \)的正方形面积,即\( 1{\mathrm{\;{cm}}}^{2} \)。
因此,被染黑的总面积为(单位:\( {\mathrm{{cm}}}^{2},\pi + 1 \))。
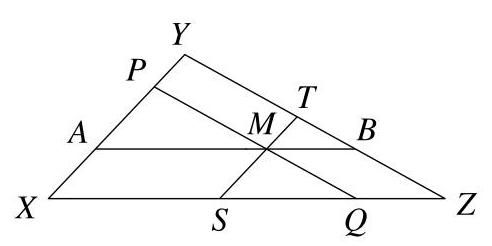
\( {AP} \) 的长度是多少?
解答
设 \( {AP},{QS} \) 与 \( {BT} \) 的公共长度为 \( x \)。
因为 \( {AB} \) 平行于 \( {XZ} \),所以对应角 \( \angle {PAM} \) 与 \( \angle {YXZ} \) 相等。又因为 \( {PQ} \) 平行于 \( {YZ} \),所以对应角 \( \angle {APM} \) 与 \( \angle {XYZ} \) 相等。
于是三角形 \( {APM} \) 与 \( {XYZ} \) 相似,因此它们的对应边成相同比例。特别地,\( \frac{AP}{XY} = \frac{AM}{XZ} \)。也就是说,\( \frac{x}{2} = \frac{AM}{4} \),从而 \( {AM} = {2x} \)。
由于 \( {AM} \) 平行于 \( {XS} \),且 \( {XA} \) 平行于 \( {SM} \),四边形 \( {MAXS} \) 为平行四边形,因此 \( {XS} = {AM} = {2x} \)。
同理,三角形 \( {MTB} \) 与 \( {XYZ} \) 相似,因此 \( \frac{TB}{YZ} = \frac{MB}{XZ} \)。于是 \( \frac{x}{3} = \frac{MB}{4} \)。从而 \( {MB} = \frac{4}{3}x \)。并且 \( {MBZQ} \) 也是平行四边形,因此 \( {QZ} = {MP} = \frac{4}{3}x \)。现在,由于 \( {XS} + {SQ} + {QZ} = {XZ} \),可得
\[ {2x} + x + \frac{4}{3}x = 4 \]
即
\[ \frac{13}{3}x = 4 \]
由此推出
\[ x = \frac{3}{13} \times 4 = \frac{12}{13}. \]
因此 \( {AP} \) 的长度为 \( \frac{12}{13} \)。
探究
\( f\left( {2015}\right) \) 的值是多少?
解答
评注
乍看之下,这似乎是一道极难的题,因为看起来需要在没有计算器的情况下求出 \( x = {2015} \) 的平方根 \( \sqrt{{x}^{2} + 1} \)!既然这绝非出题本意,我们便需另寻他法。
表达式 \( f\left( x\right) \) 中同时出现 \( x - \sqrt{{x}^{2} + 1} \) 与 \( x + \sqrt{{x}^{2} + 1} \) 两项,提示我们可以借助代数,特别是平方差公式 \( \left( {a - b}\right) \left( {a + b}\right) = {a}^{2} - {b}^{2} \),其中 \( a = x \),\( b = \sqrt{{x}^{2} + 1} \)。
若你有信心尝试此法,便会发现此题其实一点也不难。
我们有
\[ f\left( x\right) = x + \sqrt{{x}^{2} + 1} + \frac{1}{x - \sqrt{{x}^{2} + 1}}. \]
接下来,我们将 \( f\left( x\right) \) 中的两项通分,得到
\[ f\left( x\right) = \frac{\left( {x - \sqrt{{x}^{2} + 1}}\right) \left( {x + \sqrt{{x}^{2} + 1}}\right) + 1}{x - \sqrt{{x}^{2} + 1}} \]
\[ = \frac{\left( {{x}^{2} - {\left( \sqrt{{x}^{2} + 1}\right) }^{2}}\right) + 1}{x - \sqrt{{x}^{2} + 1}} \]
\[ = \frac{\left( {{x}^{2} - \left( {{x}^{2} + 1}\right) }\right) + 1}{x - \sqrt{{x}^{2} + 1}} \]
\[ = \frac{-1 + 1}{x - \sqrt{{x}^{2} + 1}} \]
\[ = \frac{0}{x - \sqrt{{x}^{2} + 1}} \]
\[ = 0\text{.} \]
无论 \( x \) 取何值,此式均成立。因此,特别地,\( f\left( {2015}\right) = 0 \)。
设这四个不同的非零数字为 \( a, b, c \) 与 \( d \)。若用它们组成 24 个不同的四位数,则 \( a, b, c \) 与 \( d \) 各在个位出现 6 次,十位出现 6 次,百位出现 6 次,千位出现 6 次。
于是,个位上的数字对 24 个数之和的贡献为 \( 6\left( {a + b + c + d}\right) \),十位上的数字贡献为 \( 6\left( {a + b + c + d}\right) \times {10} = {60}\left( {a + b + c + d}\right) \)。同理,百位上的数字贡献为 \( {600}\left( {a + b + c + d}\right) \),千位上的数字贡献为 \( {6000}\left( {a + b + c + d}\right) \)。
因此,这 24 个数的总和为
\( {6000}\left( {a + b + c + d}\right) + {600}\left( {a + b + c + d}\right) + {60}\left( {a + b + c + d}\right) + 6\left( {a + b + c + d}\right) = {6666}\left( {a + b + c + d}\right) . \)
可将 6666 作如下质因数分解:
\[ {6666} = 6 \times {1111} = 2 \times 3 \times {11} \times {101}. \]
由于\( a, b, c, d \)是四个不同的数字,它们的和最多为\( 9 + 8 + 7 + 6 = {30} \),因此这个和不包含像101这样大的素因子。我们推断,所有24个数之和\( {6666}\left( {a + b + c + d}\right) \)的最大素因子是101。
供调查
给定五个不同的非零数字,可以组成120个不同的五位数,每个数都恰好包含这五个数字。
这120个数之和的最大质因数是多少?
给定六个不同的非零数字,可以组成多少个不同的六位数,使得每个给定的数字都恰好出现一次?
所有这些六位数之和的最大质因数是多少?
这种情况可能发生的最大\( N \)值是多少?
SOLUTION
一个整数只有在与该行卡片上至少一个其他整数拥有共同质因数时,才能出现在卡片上。这排除了1(没有质因数)以及质数13、17、19和23(它们不是1到25范围内任何其他整数的因数)。
排除这五个整数后,这一行最多只能剩下20张卡片。事实上,可以将这些剩下的卡片排成一行,使得相邻卡片上的整数都拥有一个共同的素因数。做到这一点的方法很多,例如
7,14,21,3,18,15,5,25,10,4,20,24,9,6,8,12,16,2,22,11.
因此,具有所需性质的最大\( N \)值为20。
供调查
\[ 2,3,4,5,6,7,8,9,{10},{11},{12},{14},{15},{16},{18},{20},{21},{22},{24},{25} \]
排成一行,使得相邻卡片上的整数至少有一个共同的质因数。上述解法中仅给出其中一种排列方式。
在所有满足给定条件的这些整数的任意一行中,其中一个整数必须出现在末尾,即要么在最前面,要么在最后面。它是哪一个?
(i) 最大的\( N \)值是多少,使得这12张卡片中的\( N \)张可以排成一行,且任意相邻两张卡片上的数都有共同质因数?
(ii) 对于这个\( N \)值,有多少种不同的方式可以将这\( N \)张卡片排成一行以满足上述条件?
解答
评注
500的质因数分解为\( {500} = {2}^{2} \times {5}^{3} \)。由于给定函数满足公式\( f\left( {xy}\right) = f\left( x\right) + f\left( y\right) \),因此\( f\left( {500}\right) = f\left( {2 \times 2 \times 5 \times 5 \times 5}\right) = \)\( f\left( 2\right) + f\left( 2\right) + f\left( 5\right) + f\left( 5\right) + f\left( 5\right) = {2f}\left( 2\right) + {3f}\left( 5\right) . \)
因此,若能求出\( f\left( 2\right) \)和\( f\left( 5\right) \)的值,就能求出\( f\left( {500}\right) \)的值。下面给出的第一种方法直接进行计算;第二种方法更系统化,但更复杂。
方法一
将\( x = 4 \)和\( y = {10} \)代入公式\( f\left( {xy}\right) = f\left( x\right) + f\left( y\right) \),得到\( f\left( {40}\right) = f\left( 4\right) + f\left( {10}\right) \)。因此\( f\left( 4\right) = f\left( {40}\right) - f\left( {10}\right) = {20} - {14} = 6 \)。再将\( x = y = 2 \)代入公式,得到\( f\left( 4\right) = f\left( 2\right) + f\left( 2\right) \)。于是\( f\left( 2\right) = \frac{1}{2}f\left( 4\right) = \frac{1}{2} \times 6 = 3 \)。再将\( x = 2 \)和\( y = 5 \)代入公式,得到\( f\left( {10}\right) = f\left( 2\right) + f\left( 5\right) \),因此\( f\left( 5\right) = f\left( {10}\right) - f\left( 2\right) = {14} - 3 = {11} \)。
由于\( {500} = {2}^{2} \times {5}^{3} \),我们现在可以推导出\( f\left( {500}\right) = {2f}\left( 2\right) + {3f}\left( 5\right) = 2 \times 3 + 3 \times {11} = \)\( 6 + {33} = {39} \)
方法二
设\( f\left( 2\right) = a \)且\( f\left( 5\right) = b \)。由于\( {10} = 2 \times 5 \),我们有\( f\left( {10}\right) = f\left( 2\right) + f\left( 5\right) \)。由于\( {40} = {2}^{3} \times 5 \),我们有\( f\left( {40}\right) = {3f}\left( 2\right) + f\left( 5\right) \)。
因此,当\( f\left( {10}\right) = {14} \)且\( f\left( {40}\right) = {20} \)时,我们得到两个线性方程
\[ a + b = {14} \tag{1} \]
\[ {3a} + b = {20} \tag{2} \]
由方程(1)和(2)
\[ \left( {{3a} + b}\right) - \left( {a + b}\right) = {20} - {14}. \]
我们推导出\( {2a} = 6 \),因此\( a = 3 \)。于是,根据方程(1),我们有\( b = {11} \)。
由于\( {500} = {2}^{2} \times {5}^{3} \),我们推导出\( f\left( {500}\right) = {2f}\left( 2\right) + {3f}\left( 5\right) = 2 \times 3 + 3 \times {11} = {39} \)。
供探究