高级数学挑战赛

由英国数学信托基金会(United Kingdom Mathematics Trust)主办，精算师学院(Faculty Institute of Actuaries)支持

解决方案与探究

这些解答补充了我们寄往各校的纸质版答案。为方便起见，寄往学校的解答被压缩在两张A4纸内，因此往往较为简略。此处提供的解答已作扩展，部分题目还给出替代解法，并附设若干供进一步探究的问题。欢迎对这些解答提出意见，请发送至enquiry@ukmt.org.uk。

高级数学挑战赛(SMC)是一份选择题试卷。每道题给出五个选项，其中仅有一个正确。因此，你常常可以通过从给出的选项倒推，或证明其中四个不正确，来找出正确答案。在SMC的情境下，这样做是明智的。

然而，这并不能提供一个完整的数学解释，若仅给出题目而无备选答案，这样的解释便难以令人信服。因此，我们力求为每道题给出完整解答，并逐一阐明所有步骤，且不预设任何给定选项为正确。某些情况下，我们附加了评注，以提示得出该解的思考路径。正式书写解答时，你无需加入此类评注；但我们希望，去掉评注后的解答，能够成为在数学竞赛(如英国数学奥林匹克、女子数学奥林匹克及类似赛事)中呈交完整解答时的范例。

这些解答可在贵校或学院内自由使用。无需额外许可，您即可将其发布于仅限本校教职员工及学生访问的网站，在校内或学院内打印并分发纸质副本，并在课堂上使用。若您希望以其他方式使用，请先与我们联系。© UKMT 2016年11月

有关高级数学挑战赛(Senior Mathematical Challenge)的咨询请发送至:

利兹大学数学学院卫星中心，英国数学信托(UKMT)，SMC

利兹 LS2 9JT

enquiry@ukmt.org.uk www.ukmt.org.uk

---

\( \begin{array}{lllllllllllllllllllllllll} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & {10} & {11} & {12} & {13} & {14} & {15} & {16} & {17} & {18} & {19} & {20} & {21} & {22} & {23} & {24} & {25} \end{array} \)

в р в С А В А В С В Е С А В В В В Е Р Е С С Е В В

---

似乎别无他法，只能直接进行乘法运算。

\[ 9 \times {987654321} = {888888888898} \]

因此，数字9在答案中出现的次数是1。

SOLUTION

这本书在周一涨价\( {10}\% \)后价格为\( \pounds {5.50} \)，因此涨价前的价格为£5。于是，在周五降价\( {10}\% \)后，书价下降了\( {50p} \)，变为\( \pounds {4.50} \)。

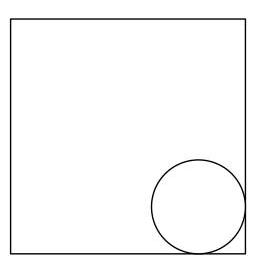
圆绕正方形滚动一圈，回到起点。

圆心移动了多远？

解答

圆滚动时，其圆心始终与正方形保持1的距离。因此，如图所示，圆心轨迹形成一个边长比原正方形小2的正方形。于是圆心移动的距离等于边长为3的正方形的周长。

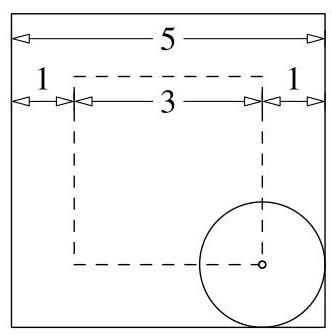
我们推断圆心移动的距离为12。

进一步探究

下列哪一项可能是亚历克斯三角形中另外两个角的差值？A 0° B 60° C 80° D 100° E 120°

SOLUTION

不等边三角形的所有边长均不同，因此所有角也均不同。

于是任意两角之差不可能为\( {0}^{ \circ } \)，这排除了选项\( \mathrm{A} \)。

三角形内角和为\( {180}^{ \circ } \)，因此亚历克斯三角形中已知一角为\( {80}^{ \circ } \)，其余两角之和为\( {100}^{ \circ } \)。于是这两角之差小于\( {100}^{ \circ } \)，这排除了选项D和E。

若两角之和为\( {100}^{ \circ } \)且差为\( {60}^{ \circ } \)，则这两个角分别为\( {80}^{ \circ } \)和\( {20}^{ \circ } \)。于是三角形将有两个角为\( {80}^{ \circ } \)，这对不等边三角形(scalene triangle)是不可能的，因此排除选项B。

因此正确选项为\( \mathrm{C} \)，因它是我们尚未排除的唯一选项。

注

在SMC(Senior Mathematical Challenge)背景下，到此即可。一旦四个选项被排除，剩下的选项必为正确。

然而，为给出完整解答，你需证明其余两角之差确实可能为\( {80}^{ \circ } \)。下面的练习4.1要求你完成此证明。

供探究

在不等边三角形(即三边长度均不同的三角形)中，所有角均互不相等。

证明此命题成立。

哪个数字位于网格中心？

三位平方数仅使用数字2、3、4、5、6。最小的此类平方数为\( {15}^{2} = {225} \)，最大的为\( {25}^{2} = {625} \)。然而，填入网格的平方数不能重复数字，因此只需考虑恰好使用2、3、4、5、6中三个不同数字的三位平方数。可验证(见下方练习5.1)满足条件的平方数仅有三个，即\( {16}^{2} = {256},{18}^{2} = {324} \)和\( {25}^{2} = {625} \)

数字2在这三个平方数中两次作为十位数字出现，因此网格中心应填数字2。

在SMC(Senior Mathematics Challenge，高级数学挑战赛)的语境下，我们可以就此止步。然而，为了给出完整解答，还需补充:由于平方数324和625恰好各用一次数字3、4、5、6，因此可以将这些数字填入方格，使它们成为平方数。图示给出了一种填法。

供探究

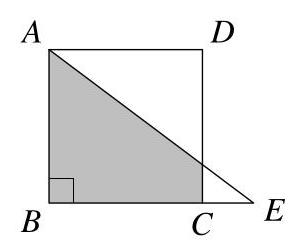
阴影区域的面积是多少？

我们设\( F \)为直线\( {AE} \)与\( {CD} \)的交点。

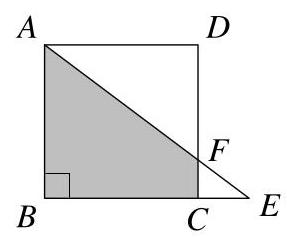
因为\( {ABCD} \)是正方形，\( \angle {BCF} = {90}^{ \circ } \)。由于同一直线上的角之和为\( {180}^{ \circ } \)，可得\( \angle {FCE} = {90}^{ \circ } \)。

于是，在三角形\( {ABE} \)和\( {FCE} \)中，我们有\( \angle {ABE} = \angle {FCE} = {90}^{ \circ } \)。同时可见\( \angle {BEA} = \angle {CEF} \)。因此这两个三角形相似。

因此

\[ \frac{FC}{AB} = \frac{CE}{BE}. \tag{1} \]

因为\( {ABCD} \)是正方形，\( {AB} = {BC} = 3 \)。我们还有\( {BE} = 4 \)。于是\( {CE} = {BE} - {BC} = \)\( 4 - 3 = 1 \)。

由方程(1)可得

\[ \frac{FC}{3} = \frac{1}{4} \]

因此\( {FC} = \frac{3}{4} \)。

阴影区域\( {ABCF} \)是一个梯形。梯形的面积由公式\( \frac{1}{2}h\left( {a + b}\right) \)给出，其中\( a \)和\( b \)是两条平行边的长度，\( h \)是这两条边之间的距离。因此梯形\( {ABCF} \)的面积为

\[ \frac{1}{2}{BC}\left( {{AB} + {FC}}\right) = \frac{1}{2}\left( {3 \times \left( {3 + \frac{3}{4}}\right) }\right) = \frac{1}{2}\left( {3 \times \frac{15}{4}}\right) = \frac{45}{8} = 5\frac{5}{8}. \]

供探究

SOLUTION

METHOD 1

我们有\( {2016}^{-1} = \frac{1}{2016} \)和\( {2016}^{-1/2} = \frac{1}{\sqrt{2016}} \)。现在，由于\( 1 < \sqrt{2016} < {2016} \)，因此

\( \frac{1}{2016} < \frac{1}{\sqrt{2016}} < 1 \)，从而\( {2016}^{-1} < {2016}^{-1/2} < 1 \)。

另一方面，\( {2016}^{0} \)等于1，而\( {2016}^{1/2} = \sqrt{2016} \)和\( {2016}^{1} = {2016} \)均大于1。

因此，在给定选项中，\( {2016}^{-1} \)的值最小。

方法二

函数\( {2016}^{x} \)可由方程定义

\[ {2016}^{x} = {e}^{x\ln {2016}}, \]

其中\( {e}^{x} \)为指数函数(见下方注释)，ln 2016 为2016的自然对数。(\( \ln {2016} \)的值为7.6089，保留四位小数。)

指数函数是增函数，即若\( x < {x}^{\prime } \)，则\( {e}^{x} < {e}^{{x}^{\prime }} \)。因此\( {2016}^{x} \)也是增函数，因为若\( x < {x}^{\prime } \)，则\( x\ln {2016} < {x}^{\prime }\ln {2016} \)，从而\( {e}^{x\ln {2016}} < {e}^{{x}^{\prime }\ln {2016}} \)。

因此，当\( - 1 < - \frac{1}{2} < 0 < \frac{1}{2} < 1 \)时，我们有\( {2016}^{-1} < {2016}^{-1/2} < {2016}^{0} < {2016}^{1/2} < {2016}^{1} \)。

因此，在给定选项中，\( {2016}^{-1} \) 是最小的。

注

对于一般实数 \( x \)，\( {e}^{x} \) 的定义相当复杂。

一种定义方式是借助无穷级数，如下所示。

\[ {e}^{x} = 1 + x + \frac{{x}^{2}}{2!} + \frac{{x}^{3}}{3!} + \cdots + \frac{{x}^{n}}{n!} + \ldots \]

若我们采用约定 \( {x}^{0} = 1 \) 和 \( 0! = 1 \)，则可改写为

\[ {e}^{x} = \frac{{x}^{0}}{0!} + \frac{{x}^{1}}{1!} + \frac{{x}^{2}}{2!} + \frac{{x}^{3}}{3!} + \cdots + \frac{{x}^{n}}{n!} + \ldots , \]

或使用求和符号表示为

\[ {e}^{x} = \mathop{\sum }\limits_{{n = 0}}^{\infty }\frac{{x}^{n}}{n!} \]

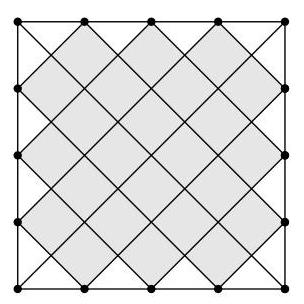
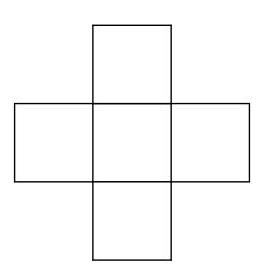
当 \( n = 7 \) 时，会形成多少个小正方形？

SOLUTION

题中所示正方形的主对角线将其分成四个象限，每个象限包含 \( 1 + 2 + 3 \) 个小正方形。因此，当 \( n = 4 \) 时，小正方形数量为 \( 4 \times \left( {1 + 2 + 3}\right) = 4 \times 6 = {24} \)，正如题目所述。

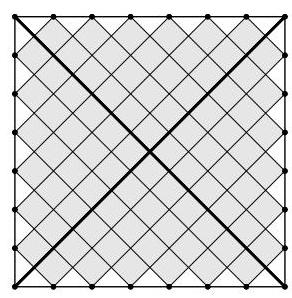
从右侧图示可见，类似地，当 \( n = 7 \) 时，小正方形数量由 \( 4 \times \left( {1 + 2 + 3 + 4 + 5 + 6}\right) = \) \( 4 \times {21} = {84} \) 给出

供探究

\[ {x}^{2} + {y}^{2} = 1,\;y = x + 1,\;y = - {x}^{2} + 1,\;y = x,\;y = \frac{1}{x} \]

有多少条图形恰好穿过正方形的两个顶点？

方法1

一种方法是绘制图形。

方程\( {x}^{2} + {y}^{2} = 1 \)的图形是以(0,0)为圆心、半径为1的圆。[根据毕达哥拉斯定理(Pythagoras’ Theorem)，坐标为(x, y)的点与点(0,0)的距离\( d \)由方程\( {x}^{2} + {y}^{2} = {d}^{2} \)给出。因此，方程\( {x}^{2} + {y}^{2} = 1 \)被那些与原点的距离为1的点满足。这些点位于以(0,0)为圆心、半径为1的圆上，如下图所示。]

方程\( y = x + 1 \)的图形是斜率为1的直线，与\( y \)轴交于点(0,1)。

方程\( y = - {x}^{2} + 1 \)的图形是一个\( \cap \)形抛物线，关于\( y \)轴对称，并经过点(0,1)。

方程\( y = x \)的图形是斜率为1的直线，经过点(0,0)。

方程\( y = \frac{1}{x} \)的图形是一个矩形双曲线(rectangular hyperbola)，以\( x \)轴和\( y \)轴为渐近线。在下图中，我们只展示了该双曲线一条臂的一部分。

这些图形如下图所示。

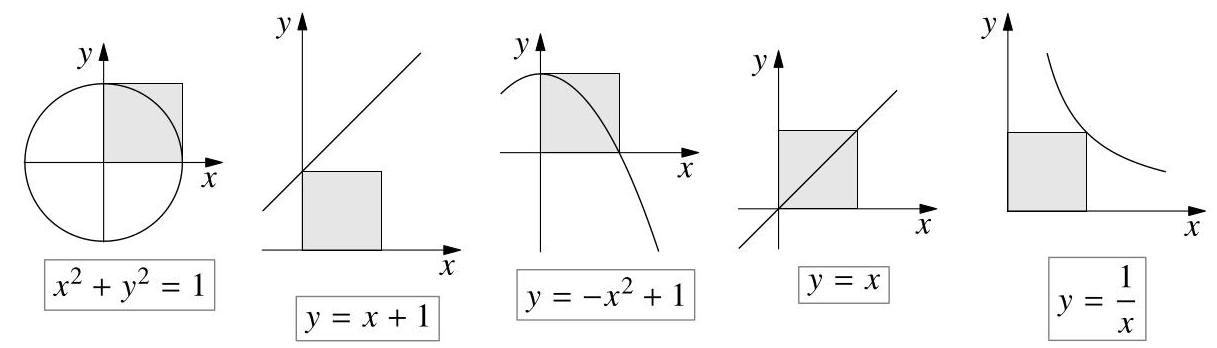
从这些图形可以看出，\( {x}^{2} + {y}^{2} = 1, y = - {x}^{2} + 1 \)和\( y = x \)的图形穿过正方形的两个顶点，而其他每个图形仅穿过正方形的一个顶点。

因此，恰好穿过正方形两个顶点的图形数量为3。注

上述解答假设我们已正确绘制图形。如需更严谨的方法，请参见下方解答。

方法2

我们通过检查正方形的某个顶点坐标是否满足图形方程，来判断给定图形是否穿过该顶点。

例如，当\( x = 0 \)且\( y = 0 \)时，我们有\( {x}^{2} + {y}^{2} \neq 1 \)。因此，\( {x}^{2} + {y}^{2} = 1 \)的图像不经过顶点(0,0)。

另一方面，当\( x = 0 \)且\( y = 1 \)时，我们有\( {x}^{2} + {y}^{2} = 1 \)。因此，\( {x}^{2} + {y}^{2} = 1 \)的图像确实经过顶点(0,1)。

在下表中，我们展示了所有这些计算的结果。如果图像经过所讨论的顶点，我们标记为“是”；否则标记为“否”。

顶点	\( {x}^{2} + {y}^{2} = 1 \)	\( y = x + 1 \)	\( y = - {x}^{2} + 1 \)	\( y = x \)	\( y = \frac{1}{x} \)
(0,0)	否	否	否	是	否
(1,0)	是	否	是	否	否
(1,1)	否	否	否	是	是
(0,1)	是	是	是	否	否

我们观察到，在所考虑的图中，有三幅图在对应列中恰好出现两次“yes”。由此推断，恰好穿过正方形两个顶点的图共有3个。

供探究

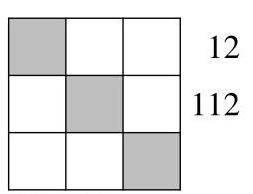
216 12

首先注意到112能被7整除，而216和12都不能被7整除。因此数字7位于第二行，但不在第一列或第二列，故7写在第二行第三列的单元格中。

因为\( {112} = 7 \times {16} \)，第二行其余两数之积为16。由于数字必须不同，这两个数字只能是2和8。又因8不是12的因数，8不能位于第二列，于是8写在第二行第一列，2写在第二行第二列。

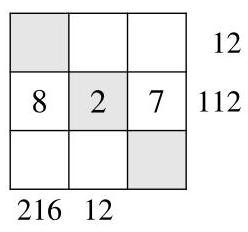
因此第二行的数字排列如图所示。

因为\( {216} = 8 \times {27} \)，第一列其余两数之积为27，故这两个数字为3和9。由于9不是12的因数，9不能位于第一行，于是9位于第一列第三行，3位于第一列第一行。

第二列三个数字的乘积为12，其中已知一个数字是2，因此该列其余两数之积为6。由于2和3已出现在表格中，这两个数字只能是1和6。

数字6不能位于第一行，否则第一行数字的乘积将不为12。因此1位于第一行第二列，6位于第三行第二列。于是第一行第三列的数字为4，剩下的数字5位于第三行第三列。

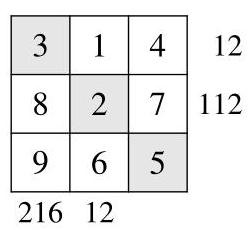
因此数字排列如图所示。阴影格中的数字为3、2和5，其乘积为30。

供探究

标记为\( X \)的方格中应填入哪个数字？

10 \( X \) 25

我们首先注意到，如果\( b \)是数字\( a \)和\( c \)的平均数，那么\( b = \frac{1}{2}\left( {a + c}\right) \)。因此\( {2b} = a + c \)，从而\( b - a = c - b \)。换句话说，数字\( a, b, c \)构成一个等差数列，即它们的差相等。

我们推断，由于网格中除10和25外的每个数都是其相邻两数的平均数，网格中的六个数构成一个等差数列。设它们的公差为\( d \)，则网格中的数将构成序列\( {10},{10} + d,{10} + {2d},{10} + {3d},{10} + {4d},{10} + {5d} \)。

由此可得\( {10} + {5d} = {25} \)，因此\( d = 3 \)。

标记为\( X \)的方格中的数字是\( {10} + {3d} \)。因为\( d = 3 \)，所以该数字为19。

SOLUTION

一个整数是平方数，当且仅当其质因数分解中每个质数的指数均为偶数。2016的质因数分解为\( {2}^{5} \times {3}^{2} \times 7 \)。

若2016是某个平方数的因数，则该平方数的质因数分解中，质数2、3和7的指数必须不小于它们在2016中的指数。

因此，以2016为因数的最小平方数的质因数分解为\( {2}^{a} \times {3}^{b} \times {7}^{c} \)，其中\( a, b \)和\( c \)分别是大于或等于5、2和1的最小偶数。因此\( a = 6, b = 2 \)且\( c = 2 \)。故以2016为因数的最小平方数为\( {2}^{6} \times {3}^{2} \times {7}^{2} \)。

现在

\[ {2}^{6} \times {3}^{2} \times {7}^{2} = {\left( {2}^{3} \times {3}^{1} \times {7}^{1}\right) }^{2} = {\left( 8 \times 3 \times 7\right) }^{2} = {168}^{2}. \]

因此，以2016为因数的最小平方数是\( {168}^{2} \)。

探究

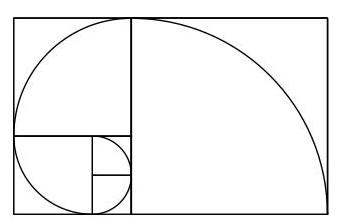
曲线的总长度是多少？

解答

这5个正方形的边长分别为1、1、2、3和5。因此曲线由五个半径分别为这些值的四分之一圆组成。半径为\( r \)的圆的周长为\( {2\pi r} \)，所以半径为\( r \)的四分之一圆弧长为\( \frac{1}{4}\left( {2\pi r}\right) \)，即\( \frac{1}{2}{\pi r} \)。

因此曲线的总长度为\( l \)，其中

\[ l = \frac{1}{2}{\pi 1} + \frac{1}{2}{\pi 1} + \frac{1}{2}{\pi 2} + \frac{1}{2}{\pi 3} + \frac{1}{2}{\pi 5} = \frac{1}{2}\pi \left( {1 + 1 + 2 + 3 + 5}\right) = {6\pi }. \]

命题“若\( n \)不是素数，则\( n - 2 \)不是素数”的反例是一个正整数\( n \)，使得该蕴含为假。形如“若\( P \)则\( Q \)”的蕴含在\( P \)为真而\( Q \)为假时为假。

因此该命题的反例是一个正整数\( n \)，使得\( n \)不是素数为真，而\( n - 2 \)不是素数为假。换句话说，反例是一个正整数\( n \)，满足\( n \)不是素数但\( n - 2 \)是素数。

由于11是素数，选项B不能提供所需的反例。

选项6、27、33和51都不是素数。然而\( 6 - 2 = 4,{27} - 2 = {25} \)和\( {51} - 2 = {49} \)也都不是素数。因此选项A、C和E均不能提供所需的反例。

这就剩下\( n = {33} \)。我们看到33不是素数，但\( {33} - 2 = {31} \)是素数。因此33是一个反例。故正确选项为D。

供探究

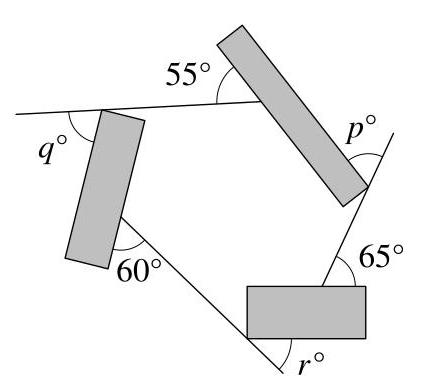
\( p + q + r \)的值是多少？

设\( P, Q \)和\( R \)为图中矩形与直线相切的点。设这些直线延长后与矩形相交于\( S, T \)和\( U \)，如图所示。

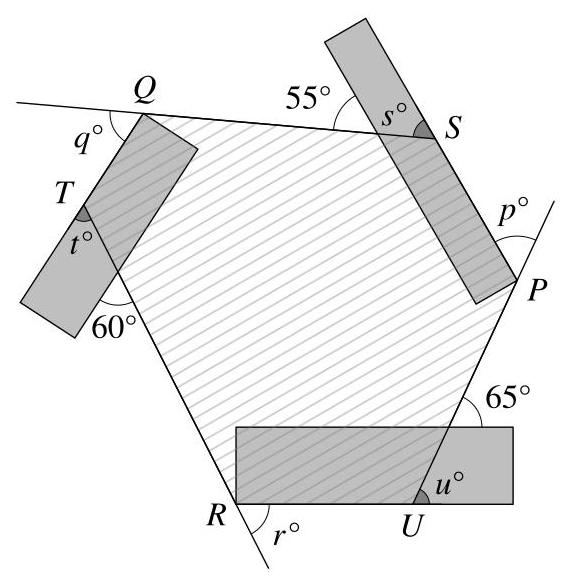
于是\( {PSQTRU} \)是一个六边形。该六边形在顶点\( P, Q \)和\( R \)处的外角分别为\( {p}^{ \circ } \)、\( {q}^{ \circ } \)和\( {r}^{ \circ } \)，如图所示。设\( S, T \)和\( U \)处的外角分别为\( {s}^{ \circ },{t}^{ \circ } \)和\( {u}^{ \circ } \)，如图所示。

六边形的外角之和为\( {360}^{ \circ } \)。因此\( p + q + r + s + t + u = {360} \)。

矩形的对边平行。当直线平行时，对应角相等。因此\( s = {55}, t = {60} \)和\( u = {65} \)。故\( s + t + u = {55} + {60} + {65} = {180} \)。

由此可得\( p + q + r = \left( {p + q + r + s + t + u}\right) - \left( {s + t + u}\right) = {360} - {180} = {180} \)。

探究

解答

我们已经在问题12的解答中看到\( {2016} = {2}^{5} \times {3}^{2} \times 7 \)。由此可得\( {2016} = \left( {{2}^{4} \times {3}^{2}}\right) \times 2 \times 7 = {\left( {2}^{2} \times 3\right) }^{2} \times 2 \times 7 = {12}^{2} \times {14} \)。因此\( \sqrt{2016} = {12}\sqrt{14} \)。

此外，\( \sqrt{56} = \sqrt{{2}^{2} \times {14}} = 2\sqrt{14} \)。因此\( \sqrt{2016} + \sqrt{56} = {12}\sqrt{14} + 2\sqrt{14} = {14}\sqrt{14} \)。

现在，\( {14}\sqrt{14} = {14}^{1} \times {14}^{1/2} = {14}^{1 + 1/2} = {14}^{3/2} \)。因此\( k = \frac{3}{2} \)。

可以选出多少个这样的代码？A 779 D 84 E 9

SOLUTION

方法一

我们计算Aaron按递增顺序选取三个数字的方法数。

我们首先考虑Aaron选择的第一个数字是1的情况。

如果他选择的第二位数字是2，那么第三位数字还有7种可选，即从3到9的所有数字(含3和9)。如果Aaron选择的第二位数字是3，那么第三位数字还有6种可选，即从4到9的所有数字(含4和9)，以此类推。最后，我们发现如果Aaron选择的第二位数字是8，那么第三位数字就只剩1种选择，即9。他不能把9选作第二位数字，因为那样第三位数字就无从选择了。

因此，Aaron 可以选择的以数字 1 开头的不同代码数量为 7 + 6 + 5 + \( 4 + 3 + 2 + 1 \)，即 28。

同样，首位数字为2的不同代码数量，Aaron可选的有6+5+4+3+2+1，即21种。

依此类推，直到最后，如果阿伦选择的第一个数字是7，他就只有一个可选的密码，即789。

因此，Aaron 可以选择的代码总数为 \( {28} + {21} + {15} + {10} + 6 + 3 + 1 \)，即 84。

方法二

该方法假设读者已具备二项式系数(binomial coefficients)的初步知识(见下方注释)。

给定任意三个不同的非零数字，亚伦只有一种方式用它们来生成密码，因为他希望将它们按升序排列。

因此，Aaron 可以选择的不同密码数量，等于他从 9 个非零数字中选取 3 个数字的不同方式数。这个数“9 选 3”写作\( \left( \begin{array}{l} 9 \\ 3 \end{array}\right) \)，有时也写作\( {}_{9}{C}_{3} \)或\( {}^{9}{C}_{3} \)。数\( \left( \begin{array}{l} 9 \\ 3 \end{array}\right) \)是\( {\left( 1 + x\right) }^{9} \)展开式中\( {x}^{3} \)的系数，它被称为二项式系数(binomial coefficient)。

二项式系数的一般公式为\( \left( \begin{array}{l} n \\ r \end{array}\right) = \frac{n!}{r!\left( {n - r}\right) !} \)。因此，Aaron 可以选择的不同密码数量为

\[ \left( \begin{array}{l} 9 \\ 3 \end{array}\right) = \frac{9!}{3!6!} = \frac{9 \times 8 \times 7}{3 \times 2 \times 1} = {84} \]

注

第二种方法利用了二项式系数“\( n \) 选 \( r \)”的公式，该公式给出了从\( n \)个不同对象中选取\( r \)个对象的方式数。你可能已经接触过由二项式系数构成的帕斯卡三角形(Pascal's triangle)。

研究这类问题的数学分支称为组合数学(Combinatorics)。由 Gerry Leversha 和 Dominic Rowland 撰写、UKMT 于 2015 年出版的《组合数学导论》(Introduction to Combinatorics)是该领域的一本优秀入门读物。

如果你们学校或学院图书馆尚未收藏此书，建议尽快采购。可通过 UKMT 官网订购。

供探究

阴影区域的面积是多少？

由于四段弧相等，它们的端点构成一个正方形，该正方形已在图中标出。

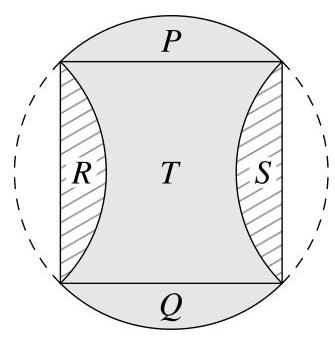
图中标出的四段弓形\( P, Q, R \)和\( S \)彼此全等。阴影区域由区域\( T \)以及弓形\( P \)和\( Q \)组成。因此，该区域的面积等于由\( T \)及两个弓形\( R \)和\( S \)构成的正方形面积。

正方形的对角线是圆的直径，因此长度为 2。于是正方形的边长为\( \sqrt{2} \)，其面积为\( \sqrt{2} \times \sqrt{2} \)，即 2。

因此，阴影区域的面积为 2。

供探究

\( m \)的最小可能值是多少？A 2 B 4 C 9 D 11 E 12

SOLUTION

设\( {WXYZ} \)为一面积非零的四边形。我们首先指出，从\( W \)到\( Z \)的最短路径是线段\( {WZ} \)。

由于\( {WXYZ} \)面积非零，点\( X \)和\( Y \)不会同时位于线段\( {WZ} \)上。因此，由线段\( {WX},{XY} \)和\( {YZ} \)组成的路径并非从\( W \)到\( Z \)的最短路线。

由此可得\( {WX} + {XY} + {YZ} > {WZ} \)。

反之，若四个正数中最小的三个之和大于最大的那个数，则必存在一个面积非零的四边形，其边长恰为这四个数。(练习19.1要求你验证这一点)

设\( h, j, k, l \)和\( m \)为五个正整数，满足\( h < j < k < l < m \)，且具有如下性质:无论从中选取哪四个数，它们都不能作为面积非零的四边形的边长。那么，无论选取哪四个数，其中最小的三个之和都不大于最大的那个数。

练习19.2要求你验证:只要\( h + j + k \leq l \)和\( j + k + l \leq m \)，整数\( h, j, k, l \)和\( m \)就满足“无论从中选取哪四个数，最小的三个之和都不大于最大的那个数”这一条件。

我们希望\( m \)尽可能小。为此，需使\( h, j, k \)和\( l \)尽可能小。\( h, j \)和\( k \)的最小可能值分别为\( h = 1, j = 2 \)和\( k = 3 \)，于是得到\( h + j + k = 1 + 2 + 3 = 6 \)。由于需满足\( h + j + k \leq l \)，\( l \)的最小可能值为6，于是\( j + k + l = 2 + 3 + 6 = {11} \)。又因需满足\( j + k + l \leq m \)，\( m \)的最小可能值为11。

供探究

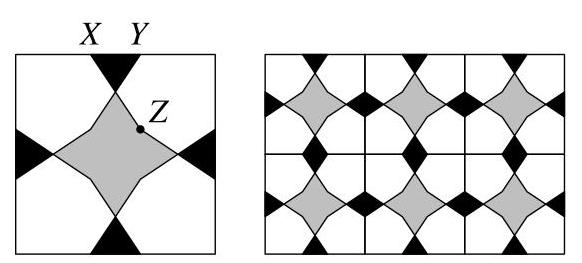
该瓷砖具有四条对称轴，每条边长为\( 8\mathrm{\;{cm}} \)。\( {XY} \)的长度为\( 2\mathrm{\;{cm}} \)。点\( Z \)满足\( {XZ} \)为一条直线，且\( {YZ} \)平行于正方形的边。

中央灰色八边形的面积是多少？

设\( T, U, V \)和\( W \)为图中标示的点。

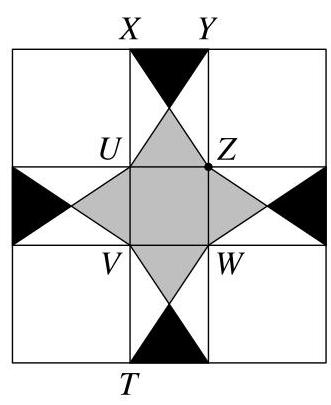
由于瓷砖具有四条对称轴，且\( {YZ} \)平行于正方形的边，因此\( {XU} \)和\( {XU} = {YZ} \)也平行于正方形的边。于是\( {XUZY} \)是一个矩形，且\( {UZ} = {XY} = 2\mathrm{\;{cm}} \)。

因为\( {XZ} \)是一条直线，根据瓷砖的对称性，\( {UY} \)也是一条直线。因此\( {XZ} \)和\( {UY} \)是矩形\( {XUZY} \)的对角线，并将该矩形分成四个面积相等的三角形。

同样，根据瓷砖的对称性，\( {UVWZ} \)是一个正方形，\( {XT} \)是一条直线，且\( {XU} = {VT} \)。因此，由于\( {UV} = {UZ} = 2\mathrm{\;{cm}} \)和\( {XT} = 8\mathrm{\;{cm}} \)，可得\( {XU} = 3\mathrm{\;{cm}} \)。

阴影八边形由\( 2\mathrm{\;{cm}} \times 2\mathrm{\;{cm}} \)正方形\( {UVWZ} \)和四个全等三角形组成。这四个三角形中每一个的面积都等于矩形\( {XUZY} \)面积的四分之一。因此，阴影八边形的面积等于\( {UVWZ} \)的面积加上\( 2\mathrm{\;{cm}} \times 3\mathrm{\;{cm}} \)矩形\( {XUZY} \)的面积。

因此，八边形的面积为\( \left( {2 \times 2 + 2 \times 3}\right) {\mathrm{{cm}}}^{2} \)，即\( {10}{\mathrm{\;{cm}}}^{2} \)。供探究

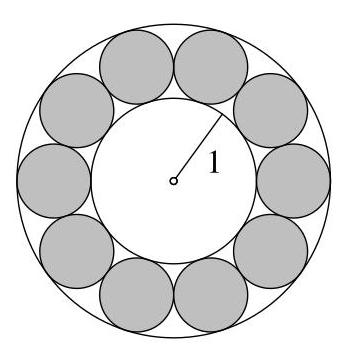
外圆的半径是多少？

解答

设\( O \)为内圆与外圆的共同圆心，\( C \)为其中一个圆盘的圆心，\( T \)为从\( O \)引出的切线与该圆盘的交点，如图所示。

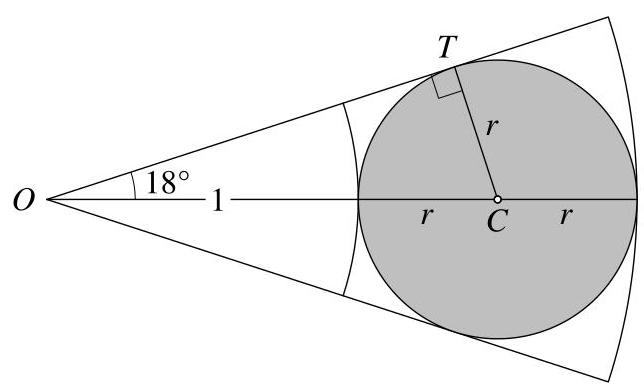
设每个圆盘的半径为\( r\mathrm{\;{cm}} \)。由图可知，外圆的半径为\( \left( {1 + {2r}}\right) \mathrm{{cm}} \)。

共有十个全等的圆盘环绕内圆。因此，从\( O \)到其中一个圆盘的两条切线之间的夹角为\( \frac{1}{10}\left( {360}^{ \circ }\right) \)，即\( {36}^{ \circ } \)。

由于\( \angle {TOC} \)是该角度的一半，我们得到\( \angle {TOC} = {18}^{ \circ } \)。

切线\( {OT} \)与半径\( {CT} \)垂直。因此，\( {TOC} \)是一个直角三角形，其斜边\( {OC} \)的长度为\( \left( {1 + r}\right) \mathrm{{cm}} \)，与角度\( {18}^{ \circ } \)相对的边长为\( r\mathrm{\;{cm}} \)。

由此可得

\[ \sin {18}^{ \circ } = \frac{r}{1 + r}. \]

由该方程我们推得

\[ \left( {1 + r}\right) \sin {18}^{ \circ } = r \]

进而得到

\[ \sin {18}^{ \circ } = \left( {1 - \sin {18}^{ \circ }}\right) r. \]

于是

\[ r = \frac{\sin {18}^{ \circ }}{1 - \sin {18}^{ \circ }}. \]

因此，外圆的半径为

\[ 1 + {2r} = 1 + \frac{2\sin {18}^{ \circ }}{1 - \sin {18}^{ \circ }} = \frac{\left( {1 - \sin {18}^{ \circ }}\right) + 2\sin {18}^{ \circ }}{1 - \sin {18}^{ \circ }} = \frac{1 + \sin {18}^{ \circ }}{1 - \sin {18}^{ \circ }}. \]

本说:“丹和卡姆中恰好有一人说真话。”

丹说:“本和卡姆中恰好有一人说真话。”

卡姆说:“本和丹都没有说真话。”

三位朋友中谁在撒谎？

解答

如果Cam的陈述为真，那么Ben和Dan都在说谎。但这样一来，Ben和Cam中恰好有一人说真话，于是Dan说真话。这构成矛盾。

我们推断Cam在说谎。

因此，Ben和Dan中至少有一人说真话。

如果Ben的陈述为真，那么Ben和Cam中恰好有一人说真话，于是Dan说真话。

同理，如果Dan的陈述为真，那么Ben说真话。

我们推断Ben和Dan说真话，而Cam在说谎。

探究

Ben说:“Cam、Dan和Sam中恰好有一人说真话。”

Dan说:“Ben、Cam和Sam中恰好有一人说真话。”

Cam说:“Ben、Dan和Sam中恰好有一人说真话。”

Sam说:“Ben、Dan和Cam中无人说真话。”

你能推断出谁说真话、谁在说谎吗？

SOLUTION

如果一个长方体被包含在半径尽可能小的球体内，长方体的顶点将位于球面上。因此，长方体的对角线将是球体的直径。所以我们首先计算\( {22} \times 2 \times {10} \)长方体的对角线长度。

考虑一个边长分别为\( a, b \)和\( c \)的一般长方体，如图所示。设\( P, Q, R \)和\( S \)为图中显示的顶点。设\( d \)为对角线\( {RS} \)的长度。

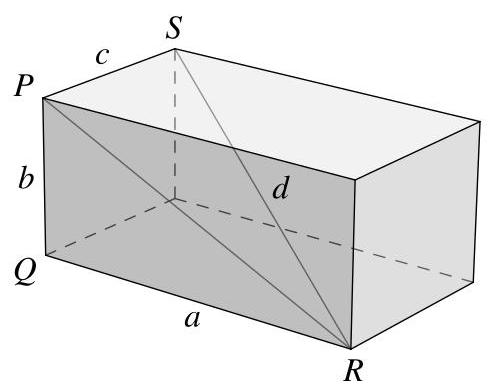
根据勾股定理，应用于直角三角形\( {PQR} \)，我们有

\[ P{R}^{2} = {a}^{2} + {b}^{2}. \]

因此，根据勾股定理，应用于直角三角形SPR，我们有

\[ {d}^{2} = P{R}^{2} + {c}^{2} = {a}^{2} + {b}^{2} + {c}^{2}. \]

由此可知，对于题目中给出的长方体，

\[ {d}^{2} = {22}^{2} + {2}^{2} + {10}^{2} = {484} + 4 + {100} = {588}. \]

因此，能容纳该长方体的最小球体的直径为\( d \)，其中\( d = \sqrt{588} \)。

设\( s \)为能放入该球体的最大立方体的边长。根据长方体对角线的方程\( {d}^{2} = {a}^{2} + {b}^{2} + {c}^{2} \)，我们有

\[ {d}^{2} = {s}^{2} + {s}^{2} + {s}^{2} \]

因此

\[ {588} = 3{s}^{2}. \]

由此可知\( {s}^{2} = {196} \)，因此\( s = {14} \)。

供研究

\[ 3{s}^{2} = {22}^{2} + {2}^{2} + {10}^{2}. \]

找出三个不同的正整数\( a, b \)和\( c \)的例子，它们除了1以外没有其他公因数，使得存在一个正整数\( s \)满足

\[ 3{s}^{2} = {a}^{2} + {b}^{2} + {c}^{2}. \]

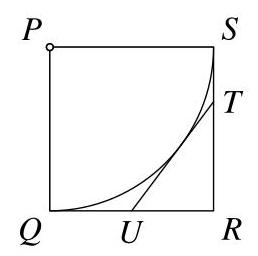
\( {TR} \)的长度与\( {UR} \)的长度之比是多少？

解答

为方便起见，由于\( U \)是\( {QR} \)的中点，我们选取单位使得正方形的边长为2。于是\( {UQ} \)和\( {UR} \)的长度均为1。

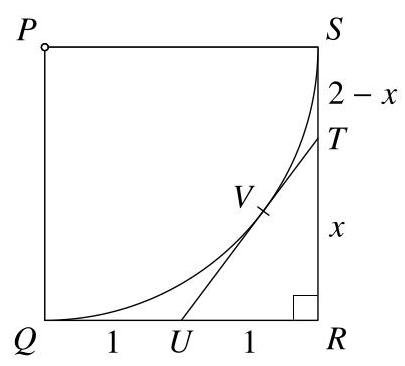
设\( {TR} \)的长度为\( x \)，则\( {TS} \)的长度为\( 2 - x \)。

设\( V \)为直线\( {TU} \)与弧相切的点。

由于从一点到圆的两条切线长度相等，\( {UV} = {UQ} = 1 \)和\( {VT} = {TS} = 2 - x \)，因此\( {UT} = {UV} + {VT} = 1 + \left( {2 - x}\right) = 3 - x \)。

在直角三角形\( {URT} \)中，斜边长度为\( 3 - x \)，其余两边长度分别为1和\( x \)。因此，根据勾股定理应用于该三角形，

\[ {1}^{2} + {x}^{2} = {\left( 3 - x\right) }^{2}. \]

由此可得

\[ 1 + {x}^{2} = 9 - {6x} + {x}^{2}, \]

从而

\[ {6x} = 8\text{.} \]

我们推导出\( x = \frac{4}{3} \)。

因此\( {TR} : {UR} = \frac{4}{3} : 1 = 4 : 3 \)。

供探究

具有2016位数的最小正整数是\( {10}^{2015} \)，即数字1后面跟着2015个0。因此，我们要求\( n \)是使\( {7n} \geq {10}^{2015} \)成立的最小正整数。于是\( n \)是满足以下条件的最小正整数:

\[ n \geq \frac{{10}^{2015}}{7} \]

\( \frac{1}{7} \)的十进制展开为循环小数0.142857，小数点后六位数字块142857无限重复。

我们有

\[ \frac{{10}^{2015}}{7} = {10}^{2015} \times \frac{1}{7}. \]

乘以\( {10}^{2015} \)的效果是将小数点向右移动2015位。因此，\( \frac{{10}^{2015}}{7} \)的十进制表示由重复块142857组成，且在小数点前有2015位数字。

现在2015\( = 6 \times {335} + 5 \)。因此，\( \frac{{10}^{2015}}{7} \)的十进制展开在小数点前有335个完整的142857块，接着是14285，而在小数点之后是数字7，随后是无限重复的142857块。即

\[ \frac{{10}^{2015}}{7} = {142857142857}\ldots {14285714285.7}\mathrm{i}{4285}\dot{7}. \]

由此可知，满足\( n \geq \frac{{10}^{2015}}{7} \)的最小整数\( n \)是

\[ \text{142857 142857 . . . 142857 14286 ,} \]

其个位数字为6。因此，使得\( {7n} \)具有2016位数字的最小正整数\( n \)的个位数字是6。

供探究