SOLUTION
我们观察到:
\( {2017} - 2 = {2015} \) 且 2015 是 5 的倍数,因此 \( {2017} - 2 \) 不是质数。
\( {2017} - 1 = {2016} \) 且 2016 是 2 的倍数,因此 \( {2017} - 1 \) 不是质数。
\( {2017} + 1 = {2018} \) 且 2018 是 2 的倍数,因此 \( {2017} + 1 \) 不是质数。
\( {2017} + 2 = {2019} \) 且 2019 是 3 的倍数,因此 \( {2017} + 2 \) 不是质数。
已知给出的选项中有一个是质数,因此可推断剩下的选项 2017 是质数。
供探究
然而,若无此假设,若想证明 2017 是质数,则需检查 2017 不存在小于 2017 的质因数。
为了证明 2017 是质数,我们需检查的最大质数 \( p \) 是多少,以确保它不是 2017 的因数?
为什么这种能被 3 整除的检验方法成立?
(b) 最小的正整数 \( n \) 是多少,使得 \( {2017} - n \) 和 \( {2017} + n \) 都是质数?
戴夫的单位长度质量是多少?
解答
戴夫的单位长度质量为\( \frac{26}{40}\mathrm{\;g}/\mathrm{{cm}} \)。我们有
\[ \frac{26}{40} = \frac{26}{{10} \times 4} = \frac{2.6}{4} = {0.65} \]
因此戴夫的单位长度质量为\( {0.65}\mathrm{\;g}/\mathrm{{cm}} \)。
SOLUTION
设新排列中的整数依次为\( p, q, r, s, t \)。因为前三个整数之和与后三个整数之和相等,
\[ p + q + r = r + s + t, \]
于是
\[ p + q = s + t \]
因此我们看到整数对\( p, q \)的和与整数对\( s, t \)的和相同。同时,中间数\( r \)是不在这两个对中的那个数。
容易验证\( 2 + 9 = 5 + 6 \),且2,9和5,6是给定整数中唯一两对和相等的组合。
因此新排列中的中间整数是14,因为它不出现在任何一对中。供探究
(b) 从1到20(含)的所有正整数集合中,最多可以选出多少个整数,使得选出的整数中任意两对的和都不相同?
将2017和\( \frac{1}{2017} \)写成同分母,我们得到
\[ {2017} - \frac{1}{2017} = \frac{{2017}^{2} - 1}{2017}. \]
现在,
\[ {2017}^{2} - 1 = {2017}^{2} - {1}^{2}. \]
因此,利用平方差的标准因式分解,我们得到
\[ {2017} - \frac{1}{2017} = \frac{{2017}^{2} - {1}^{2}}{2017} = \frac{\left( {{2017} + 1}\right) \left( {{2017} - 1}\right) }{2017} = \frac{{2018} \times {2016}}{2017}. \]
大约是多少英里?
SOLUTION
十亿是\( {1000} \times {1000000} = {10}^{3} \times {10}^{6} = {10}^{3 + 6} = {10}^{9} \)。因此134亿光年就是\( {13.4} \times {10}^{9} \)光年。由于一光年约为\( 6 \times {10}^{12} \)英里,134亿光年约为
\[ \left( {6 \times {10}^{12}}\right) \times \left( {{13.4} \times {10}^{9}}\right) \text{light-years.} \]
现在
\[ \left( {6 \times {10}^{12}}\right) \times \left( {{13.4} \times {10}^{9}}\right) = \left( {6 \times {13.4}}\right) \times \left( {{10}^{12} \times {10}^{9}}\right) . \]
现在\( 6 \times {13.4} \)约为80,因此\( \left( {6 \times {13.4}}\right) \times \left( {{10}^{12} \times {10}^{9}}\right) \)约为
\[ {80} \times \left( {{10}^{12} \times {10}^{9}}\right) \text{.} \]
最后,我们得到
\[ {80} \times \left( {{10}^{12} \times {10}^{9}}\right) = 8 \times {10} \times {10}^{{12} + 9} = 8 \times {10} \times {10}^{21} = 8 \times {10}^{22}. \]
因此134亿光年约为\( 8 \times {10}^{22} \)英里。
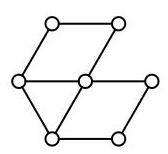
所需的最少颜色数量是多少?
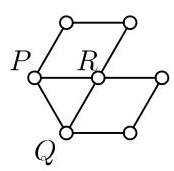
右侧图中标记为\( P, Q \)和\( R \)的每对圆都用线段连接。因此这三个圆必须用不同颜色着色。所以至少需要三种颜色。
右侧的图(为清晰起见放大了圆)展示了一种用三种颜色给圆着色的方法,使得用线段连接的圆颜色不同。
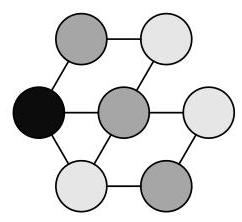
因此3是所需的最少颜色数量。
供探究
找出一个由线段连接的圆排列,使得需要四种颜色。
这种排列中最少的圆数是多少?
注
关于平面地图的四色定理(Four Colour Theorem)的第一个证明由Kenneth Appel和Wolfgang Haaken于1977年发表。他们的证明将一般情形归结为1482个不可避免的配置,这些配置需要分别验证。这些配置由计算机程序生成并检查。自1977年以来,人们找到了更简单的使用计算机的证明。但尚未有人找到一个足够简单、能让人类在合理时间内仅用纸笔检查的证明。
一本关于四色定理的好书是《四种颜色就够了:地图问题是如何解决的》(Four Colours Suffice: How the Map Problem was Solved),Robin Wilson,2002年。7. 正整数\( k \)满足方程\( \sqrt{2} + \sqrt{8} + \sqrt{18} = \sqrt{k} \)。\( k \)的值是多少?A 28 B 36 C 72 D 128 E 288 解答
因为\( 8 = {2}^{2} \times 2 \)和\( {18} = {3}^{2} \times 2 \),我们有\( \sqrt{8} = 2\sqrt{2} \)和\( \sqrt{18} = 3\sqrt{2} \)。因此
\[ \sqrt{2} + \sqrt{8} + \sqrt{18} = \sqrt{2} + 2\sqrt{2} + 3\sqrt{2} \]
\[ = 6\sqrt{2} \]
\[ = \sqrt{{6}^{2} \times 2} \]
\[ = \sqrt{72}\text{. } \]
因此\( k = {72} \)。
解答
我们有
\[ {1}^{-1} = \frac{1}{1} = 1 \]
\[ {4}^{-\frac{1}{2}} = \frac{1}{{4}^{\frac{1}{2}}} = \frac{1}{\sqrt{4}} = \frac{1}{2} \]
\[ {6}^{0} = 1\text{,} \]
\[ {8}^{\frac{2}{3}} = {\left( {8}^{\frac{1}{3}}\right) }^{2} = {\left( \sqrt[3]{8}\right) }^{2} = {2}^{2} = 4, \]
并且
\[ {16}^{\frac{3}{4}} = {\left( {16}^{\frac{1}{4}}\right) }^{3} = {\left( \sqrt[4]{16}\right) }^{3} = {2}^{3} = 8. \]
因此我们看到,只有选项 B 的表达式在计算后得到的数不是整数。
供探究
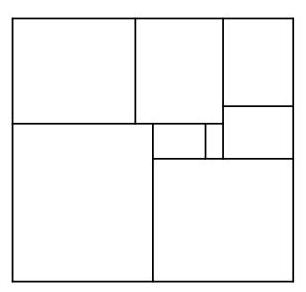
\( n \) 的值是多少?
解答
尺寸为 \( k \times \left( {k + 1}\right) \) 的矩形总面积,对于 \( k = 1,2,3,4,5,6,7,8 \),为
\( 1 \times 2 + 2 \times 3 + 3 \times 4 + 4 \times 5 + 5 \times 6 + 6 \times 7 + 7 \times 8 + 8 \times 9 = 2 + 6 + {12} + {20} + {30} + {42} + {56} + {72} \)
\[ = {240} \]
\[ = {15} \times {16}\text{.} \]
因此 \( n = {15} \)。
在 SMC 的语境下,上述计算足以表明,若较小的矩形铺满一个尺寸为 \( n \times \left( {n + 1}\right) \) 的矩形,且 \( n \) 为某个整数,则 \( n = {15} \)。
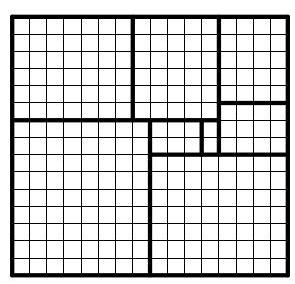
然而,为了得到完整的解答,还需证明这八个小矩形能够拼成一个\( {15} \times {16} \)的矩形。
从题目中的图来看,这似乎可行。右侧的图进一步确认了各矩形的尺寸无误。
同时请注意,从该图可直接看出大矩形的尺寸为\( {15} \times {16} \)。
供探究
换句话说,求下列和式的公式
\[ 1 \times 2 + 2 \times 3 + 3 \times 4 + \cdots + s \times \left( {s + 1}\right) . \]
[注意,使用\( \sum \)记号,可将该和式写成
\[ \mathop{\sum }\limits_{{k = 1}}^{s}k \times \left( {k + 1}\right) \text{, or, suppressing the multiplication sign, as}\mathop{\sum }\limits_{{k = 1}}^{s}k\left( {k + 1}\right) \rbrack \text{.} \]
(b) 验证当\( s = 8 \)时,你的公式给出的结果为240。
\[ \mathop{\sum }\limits_{{k = 1}}^{s}k\left( {k + 1}\right) = n\left( {n + 1}\right) ? \]
(b) 对于你在(a)中找到的\( s \)值,能否用尺寸为\( k \times \left( {k + 1}\right) \)的矩形(其中\( k \)取1到\( s \)的所有整数)拼成一个\( n \times \left( {n + 1}\right) \)的矩形?
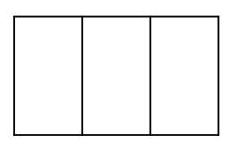
如图所示。
每个小矩形都与大矩形相似。
在这四个矩形中,较长边与较短边的长度之比是多少?
较长边与较短边的长度之比是多少?
我们假设三个较小矩形的长边长度为\( x \),短边长度为\( y \)。

由此可知,大矩形的长边长度为\( {3y} \),短边长度为\( x \)。
因为较小矩形与大矩形相似\( \frac{x}{y} = \frac{3y}{x} \),因此\( \frac{{x}^{2}}{{y}^{2}} = \frac{3}{1} \)。
于是\( \frac{x}{y} = \frac{\sqrt{3}}{1} \)。
因此,所有矩形中长边与短边的长度比均为\( \sqrt{3} : 1 \)。
供探究
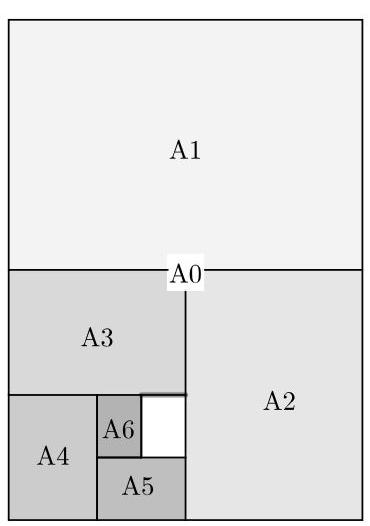
最大尺寸为\( \mathrm{A}0 \)。
将一张A0纸沿平行于短边的直线对半裁切,得到两张A1纸。
以同样方式将一张A1纸对半裁切,得到两张A2纸,依此类推,如图所示。
所有这些纸张的形状均为相似矩形。
(a) 这些矩形中长边与短边的长度比是多少?
(b) 一张A0纸的面积为\( 1{\mathrm{\;m}}^{2} \)。求A0纸的长边和短边长度,精确到\( \mathrm{{cm}} \)。
(c) 这些尺寸中最常用的是A4。求A4纸的长边和短边长度,精确到\( \mathrm{{cm}} \)。
(d) 标准纸张的克重为\( {80}\mathrm{\;g}/{\mathrm{m}}^{2} \)。一张标准A4纸的重量是多少?
他们年龄的平方差等于他们年龄之和的四倍。
他们年龄之和等于他们年龄之差的八倍。
两人中较大的年龄是多少?
设两位青少年的年龄分别为\( a \)和\( b \),且\( a > b \)。
因为他们年龄的平方差等于他们年龄之和的四倍
\[ {a}^{2} - {b}^{2} = 4\left( {a + b}\right) . \]
通过因式分解其左侧,可将上式改写为
\[ \left( {a - b}\right) \left( {a + b}\right) = 4\left( {a + b}\right) \]
由于\( a + b \neq 0 \),可将上式两边同除以\( a + b \),得到
\[ a - b = 4 \tag{1} \]
因为他们年龄之和是他们年龄之差的八倍
\[ a + b = 8\left( {a - b}\right) \]
因此,由(1)得
\[ a + b = {32} \tag{2} \]
将方程(1)与(2)相加,得到
\[ {2a} = {36} \]
从而
\[ a = {18}\text{.} \]
因此,两位青少年中较大的年龄为18。
探究
用\( k \)和\( n \)表示这两位青少年的年龄公式。验证你的公式在问题11及习题11.1和11.2中给出正确答案。
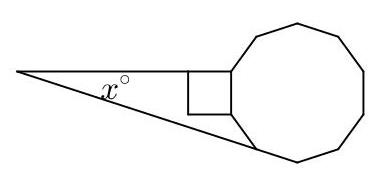
SOLUTION
我们考虑右侧图中所示的四边形\( {PQRS} \)。因为\( {PQRS} \)是四边形,其内角总和为\( {360}^{ \circ } \)。
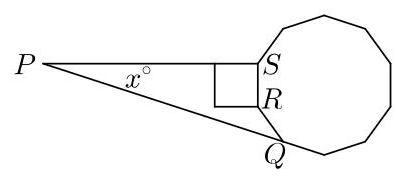
由于它是十边形的外角,\( \angle {RQP} = \)\( \frac{1}{10} \times {360}^{ \circ } = {36}^{ \circ } \)。
因此十边形的内角为\( {\left( {180} - {36}\right) }^{ \circ } = {144}^{ \circ } \)。于是优角\( {SRQ} \)为\( {\left( {360} - {144}\right) }^{ \circ } = {216}^{ \circ } \)。角\( {PSR} \)是正方形的一个角,因此为\( {90}^{ \circ } \)。
因此,我们有
\[ {x}^{ \circ } + {36}^{ \circ } + {216}^{ \circ } + {90}^{ \circ } = {360}^{ \circ }. \]
于是
\[ {x}^{ \circ } = {\left( {360} - {342}\right) }^{ \circ } = {18}^{ \circ }\text{.} \]
供探究
乔希:“杰诺坦有罪。” 蒂根:“伊泽贝尔是无辜的。”
只有有罪者在说谎;其余人都在说真话。
谁有罪?
需要更多信息
解答
只有一人有罪,因此要么Genotan在说谎,要么Josh在说谎。若Josh说谎,则Genotan无罪,从而说真话,于是Tegan有罪,这与“仅一人有罪”矛盾。因此Josh没有说谎,故Genotan是有罪者。
探究
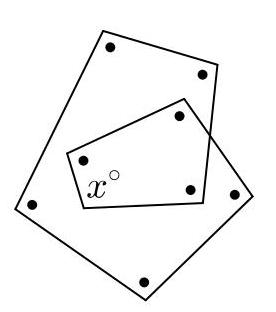
\( x \)的值是多少?
\( \begin{array}{lllll} \text{ A }{100} & \text{ B }{105} & \text{ C }{110} & \text{ D }{115} & \text{ E }{120} \end{array} \)
解法A
方法1
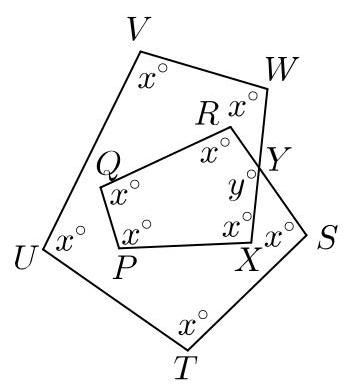
我们按下图所示给图形的顶点标号。
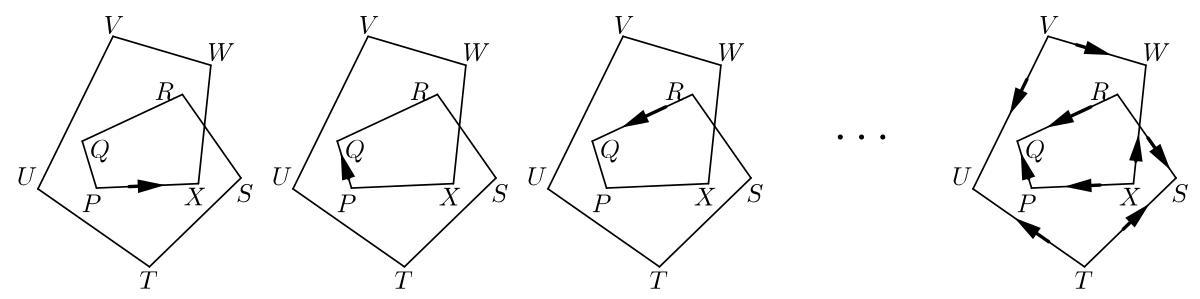
我们在最左上图所示方向沿\( {PX} \)放置一支箭头。将此箭头绕点\( P \)逆时针旋转,直至其沿\( {PQ} \)指向上方第二图所示方向。箭头已逆时针旋转了角\( {x}^{ \circ } \)。
接着我们将箭头绕点\( Q \)逆时针旋转,直至其沿\( {RQ} \)指向上方第三图所示方向。由于所有标记为\( \bullet \)的角均为\( {x}^{ \circ } \),箭头再次逆时针旋转了\( {x}^{ \circ } \)。
我们继续此过程,依次绕点\( R, S, T \)、\( U, V, W \)、\( X \)将箭头逆时针旋转\( {x}^{ \circ } \)。最终箭头沿\( {XP} \)指向最右图所示方向。
在此图中,我们还标出了箭头在整个过程中除初始位置外在其他各边上的指向。
可见,在此过程中箭头共旋转了\( 2\frac{1}{2} \)整圈,因此其总旋转角为\( 2\frac{1}{2} \times {360}^{ \circ } \),即\( {900}^{ \circ } \)。箭头共旋转了9次,每次旋转角为\( {x}^{ \circ } \)。
因此\( {9x} = {900} \),从而\( x = {100} \)。
方法二
我们令\( Y \)为\( {RS} \)与\( {WX} \)的交点,并设\( \angle {RYX} = {y}^{ \circ } \)。
五边形的内角和为\( {540}^{ \circ } \)。在五边形\( {PXYRQ} \)中,顶点\( Y \)处的内角为\( {y}^{ \circ } \),其余四个角均为\( {x}^{ \circ } \)。因此我们有
\[ {4x} + y = {540}\text{. (1). } \tag{1.} \]
六边形的内角和为\( {720}^{ \circ } \)。在六边形\( {SYWVUT} \)中,顶点\( Y \)处的优角(reflex angle)为\( {360}^{ \circ } - {y}^{ \circ } \),其余五个角均为\( {x}^{ \circ } \)。
因此\( {5x} + \left( {{360} - y}\right) = {720} \),从而
\[ {5x} - y = {360}\text{.} \tag{2} \]
将方程(1)与(2)相加,我们推得\( {9x} = {900} \)。因此\( x = {100} \)。
供探究
证明该公式正确。
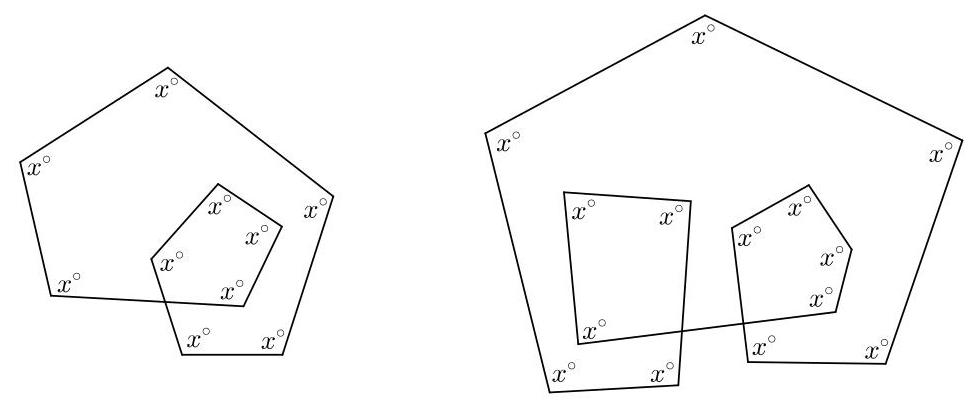
(a) 上左图中有10个标记角,均等于\( {x}^{ \circ } \)。\( x \)的值是多少?
(b) 上右图中有14个标记角,均等于\( {x}^{ \circ } \)。\( x \)的值是多少?
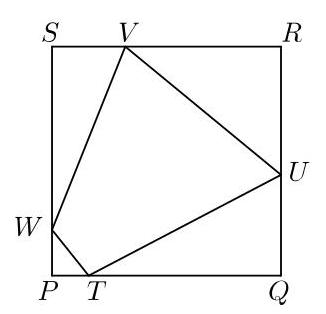
\( {TUVW} \)的面积是\( {PQRS} \)的一半。
\( {PQ} \)的长度是多少?
我们设正方形\( {PQRS} \)的边长为\( x \)。那么\( {TQ},{UR},{VS} \)和\( {WP} \)的长度分别为\( x - 1, x - 2, x - 3 \)和\( x - 4 \)。
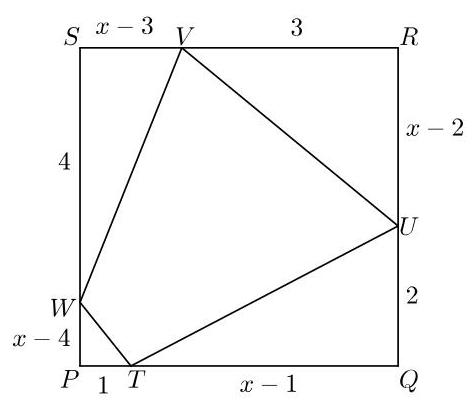
正方形\( {PQRS} \)的面积为\( {x}^{2} \)。\( {TUVW} \)的面积是它的一半。因此,三角形\( {PTW},{TQU},{URV} \)和\( {VSW} \)的面积之和也是正方形面积的一半,从而该和等于\( \frac{1}{2}{x}^{2} \)。
三角形的面积等于底与高的乘积的一半。因此我们有
\[ \frac{1}{2}\left( {1 \times \left( {x - 4}\right) }\right) + \frac{1}{2}\left( {2 \times \left( {x - 1}\right) }\right) + \frac{1}{2}\left( {3 \times \left( {x - 2}\right) }\right) + \frac{1}{2}\left( {4 \times \left( {x - 3}\right) }\right) = \frac{1}{2}{x}^{2}. \]
该方程化简得
\[ {10x} - {24} = {x}^{2}, \]
于是
\[ {x}^{2} - {10x} + {24} = 0. \]
上式左侧可因式分解为
\[ \left( {x - 4}\right) \left( {x - 6}\right) = 0\text{.} \]
故\( x = 6 \)或\( x = 4 \)。
为了如图中那样存在四个三角形,\( x > 4 \)。因此我们推断\( x = 6 \)。于是\( {PQ} \)的长度为6。
供探究
此时\( {PQ} \)的长度是多少?
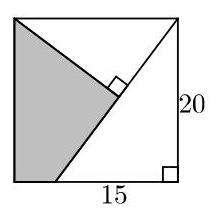
阴影四边形的面积是多少?
SOLUTION
我们设正方形的顶点为\( P, Q, R \)和\( S \),点\( T \)和\( U \)如图所示。
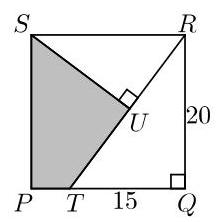
我们首先指出,根据毕达哥拉斯定理(Pythagoras' Theorem),应用于直角三角形\( {TQR} \),
\[ R{T}^{2} = {15}^{2} + {20}^{2} = {225} + {400} = {625} = {25}^{2}. \]
于是\( {RT} = {25} \)。
因为\( {SR} \)平行于\( {PQ} \),所以内错角\( \angle {SRU} \)与\( \angle {QTU} \)相等。因此,直角三角形\( {SUR} \)与\( {RQT} \)相似,于是它们的对应边成
比例。因此
\[ \frac{SR}{RT} = \frac{SU}{RQ} = \frac{RU}{TQ}. \]
现在\( {SR} = {RQ} = {20} \)。因此
\[ \frac{20}{25} = \frac{SU}{20} = \frac{RU}{15}. \]
于是\( {SU} = {16} \)且\( {RU} = {12} \)。
阴影四边形的面积等于正方形\( {PQRS} \)的面积减去三角形\( {SUR} \)和\( {RQT} \)的面积。因此阴影四边形的面积为
\[ {20}^{2} - \frac{1}{2}\left( {{16} \times {12}}\right) - \frac{1}{2}\left( {{20} \times {15}}\right) = {400} - {96} - {150} = {154}. \]
NOTE
另一种求\( {RT} \)长度的方法是注意到\( {TQ} \)与\( {QR} \)的长度之比为\( 3 : 4 \),因此直角三角形\( {TQR} \)是一个按因子5放大的(3,4,5)三角形。于是\( {RT} \)的长度为\( 5 \times 5 = {25} \)。
又因为三角形\( {RUS} \)与三角形\( {TQR} \)相似,且斜边长为20,所以\( {RUS} \)是一个按因子4放大的(3,4,5)三角形。于是\( {RU} \)的长度为\( 4 \times 3 = {12} \),\( {SU} \)的长度为\( 4 \times 4 = {16} \)。
供探究
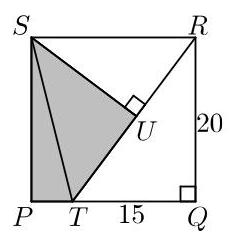
验证这两个面积之和为154。
克莱尔一开始有40颗糖果。
贝丝最初有多少颗糖果?
解法
我们从最终情形倒推:当艾米、贝丝和克莱尔最终拥有相同数量的糖果时,设\( s \)为她们最终各自拥有的糖果数。
克莱尔最终有\( s \)颗糖果。因此,在她把三分之一糖果给艾米之前,克莱尔有\( t \)颗糖果,其中\( \frac{2}{3}t = s \)。由此得\( t = \frac{3}{2}s \)。我们推断,在给艾米三分之一糖果之前,克莱尔有\( \frac{3}{2}s \)颗糖果,并给出其中的三分之一,即\( \frac{1}{2}s \)颗糖果给艾米。因此,在收到这些糖果之前,艾米有\( \frac{1}{2}s \)颗糖果。
同理,贝丝在把三分之一糖果给克莱尔后最终有\( s \)颗糖果。因此,在此之前她有\( \frac{3}{2}s \)颗糖果。由于克莱尔在从贝丝处收到\( \frac{1}{2}s \)颗糖果后有\( \frac{3}{2}s \)颗糖果,她在此之前有\( s \)颗糖果。
由此可知,在艾米把三分之一糖果给贝丝之后,艾米有\( \frac{1}{2}s \)颗糖果,贝丝有\( \frac{3}{2}s \)颗糖果,克莱尔有\( s \)颗糖果。
因此,在艾米把三分之一糖果给贝丝之前,艾米有\( \frac{3}{4}s \)颗糖果。她给贝丝\( \frac{1}{4}s \)颗糖果。因此,在收到这些糖果之前,贝丝有\( \frac{3}{2}s - \frac{1}{4}s = \frac{5}{4}s \)颗糖果。
我们可以用下表总结上述过程。
| 阶段 | 艾米 | 贝丝 | 克莱尔 |
| 克莱尔之后的最终糖果分配 | |||
| 将她三分之一的糖果(\( \frac{1}{2}s \)颗糖果)给艾米。贝丝给出后的糖果分配 | \( S \) | \( S \) | \( S \) |
| 她三分之一的糖果\( \left( {\frac{1}{2}s\text{sweets}}\right) \)给克莱尔。 | \( \frac{1}{2}S \) | \( S \) | \( \frac{3}{2}S \) |
| 艾米将她三分之一的糖果(\( \frac{1}{4}s \)颗糖果)给贝丝后的糖果分配。 | \( \frac{1}{2}S \) | \( \frac{3}{2}S \) | \( S \) |
| 初始糖果分配。 | \( \frac{3}{4}S \) | \( \frac{5}{4}S \) | \( S \) |
我们被告知克莱尔(Claire)一开始有40颗糖果。因此\( s = {40} \)。所以贝丝(Beth)一开始有\( \frac{5}{4}\left( {40}\right) = {50} \)颗糖果。
供探究
对于两个特定值\( x \)和\( y \),且\( x > y \),其比值\( A : G = 5 : 4 \)。
对于这些\( x \)和\( y \)的值,比值\( x : y \)是多少?
解答
我们被告知
\[ \frac{\frac{1}{2}\left( {x + y}\right) }{\sqrt{xy}} = \frac{5}{4}. \]
因此
\[ 2\left( {x + y}\right) = 5\sqrt{xy}. \]
通过将该方程两边平方,我们推导出
\[ 4{\left( x + y\right) }^{2} = {25xy} \]
通过展开上述方程的左侧,我们得到
\[ 4\left( {{x}^{2} + {2xy} + {y}^{2}}\right) = {25xy} \]
或等价地
\[ 4{x}^{2} + {8xy} + 4{y}^{2} = {25xy}. \]
因此
\[ 4{x}^{2} - {17xy} + 4{y}^{2} = 0. \]
上述方程左侧可因式分解为
\[ \left( {{4x} - y}\right) \left( {x - {4y}}\right) = 0\text{.} \]
因此
\[ {4x} = y\text{or}x = {4y}\text{.} \]
因此,由于\( x > y \),
\[ x = {4y}\text{.} \]
故
\[ x : y = 4 : 1\text{.} \]
供探究
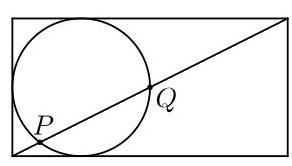
弦\( {PQ} \)的长度是多少?
解法 B
设矩形的顶点为\( K, L, M \)和\( N \),如图示。设\( O \)为圆心,\( R \)为从\( O \)到弦\( {PQ} \)的垂足。
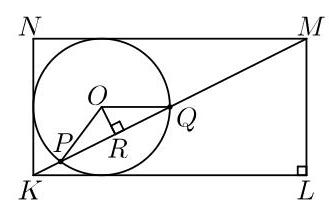
首先,根据勾股定理(Pythagoras' Theorem)应用于直角三角形\( {KLM}, K{M}^{2} = K{L}^{2} + L{M}^{2} = {4}^{2} + {2}^{2} = {20} \)。
因此\( {KM} = \sqrt{20} = 2\sqrt{5} \)。
半径\( {OQ} \)平行于\( {KL} \)。(题19.1要求你证明这一点。)因此,内错角\( \angle {OQR} \)与\( \angle {MKL} \)相等。于是直角三角形\( {OQR} \)与
\( {MKL} \)相似。特别地,
\[ \frac{RQ}{OQ} = \frac{KL}{KM} \]
由此可得
\[ {RQ} = \frac{KL}{KM} \times {OQ} = \frac{4}{2\sqrt{5}} \times 1 = \frac{2}{\sqrt{5}}. \]
直角三角形\( {ORQ} \)与\( {ORP} \)全等,因为它们共享边\( {OR} \),且斜边\( {OQ} \)与\( {OP} \)相等(同为该圆的半径)。因此\( {PR} = {RQ} = \frac{2}{\sqrt{5}} \)。于是我们得出
\[ {PQ} = {PR} + {RQ} = \frac{2}{\sqrt{5}} + \frac{2}{\sqrt{5}} = \frac{4}{\sqrt{5}}. \]
供探究
问题19也可利用定理(见问题19.3)求解,该定理指出\( K{T}^{2} = \)\( {KP} \times {KQ} \)。
说明如何利用该等式求弦\( {PQ} \)的长度。
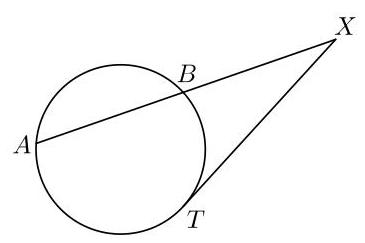
若圆的一条弦\( {AB} \)与点\( T \)处的切线相交于圆外一点\( X \),则
\[ {AX} \times {BX} = T{X}^{2}. \]
找出该定理的一个证明。
你可以自行寻找证明,向老师请教,或在书籍、网络上查找。
在几何书《Crossing the Bridge》(作者Gerry Leversha,UKMT出版)第97页可找到对该定理的讨论。
(访问:http://shop.ukmt.org.uk/ukmt-books/)
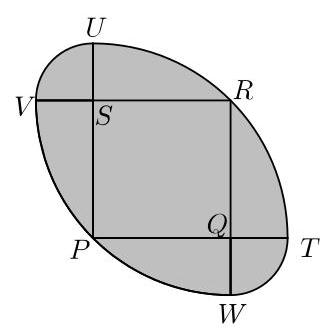
阴影区域周长是多少?
解法B
正方形\( {PQRS} \)的边长为1,因此其对角线\( {PR} \)的长度为\( \sqrt{2} \)。于是以\( P \)为圆心、\( \sqrt{2} \)为半径的弧\( {TRU} \)是一个四分之一圆,其弧长为\( \frac{1}{4} \times {2\pi }\sqrt{2} \),即\( \frac{1}{2}\sqrt{2}\pi \)。
同理,弧\( {VPW} \)的长度为\( \frac{1}{2}\sqrt{2}\pi \)。
弧\( {UV} \)的半径等于\( {SU} \)的长度。由于\( {PU} \)的长度为\( \sqrt{2} \),\( {PS} \)的长度为1,因此\( {SU} \)的长度为\( \sqrt{2} - 1 \)。弧\( {UV} \)是以该半径为半径的四分之一圆,故其弧长为\( \frac{1}{4} \times {2\pi }\left( {\sqrt{2} - 1}\right) \),即\( \frac{1}{2}\left( {\sqrt{2} - 1}\right) \pi \)。
同理,弧\( {WT} \)的长度为\( \frac{1}{2}\left( {\sqrt{2} - 1}\right) \pi \)。
因此,阴影区域周长的总长度为
\[ \frac{1}{2}\sqrt{2}\pi + \frac{1}{2}\sqrt{2}\pi + \frac{1}{2}\left( {\sqrt{2} - 1}\right) \pi + \frac{1}{2}\left( {\sqrt{2} - 1}\right) \pi = \left( {2\sqrt{2} - 1}\right) \pi . \]
供探究
方程\( {4}^{x} = {y}^{2} + {15} \)可整理为\( {4}^{x} - {y}^{2} = {15} \)。此时\( {4}^{x} = {\left( {2}^{2}\right) }^{x} = {\left( {2}^{x}\right) }^{2} \)。因此\( {4}^{x} - {y}^{2} \)可利用平方差公式的标准分解进行因式分解,从而将方程改写为
\[ \left( {{2}^{x} - y}\right) \left( {{2}^{x} + y}\right) = {15} \]
于是,要使(x, y)成为原方程的正整数解,\( {2}^{x} - y \)和\( {2}^{x} + y \)必须是乘积为15的正整数,且满足\( {2}^{x} - y < {2}^{x} + y \)。
因此,唯一可能的情形是
\[ {2}^{x} - y = 1\text{ and }{2}^{x} + y = {15}, \]
或者
\[ {2}^{x} - y = 3\text{ and }\;{2}^{x} + y = 5. \]
第一种情形中,\( {2}^{x} = 8 \)和\( y = 7 \),得到\( x = 3 \)和\( y = 7 \)。
第二种情形中,\( {2}^{x} = 4 \)和\( y = 1 \),得到\( x = 2 \)和\( y = 1 \)。
因此,满足方程\( {4}^{x} = {y}^{2} + {15} \)的正整数对恰好有两组,即(3,7)和(2,1)。
供探究
(b) 验证:若\( {2}^{x} - y = 3 \)且\( {2}^{x} + y = 5 \),则\( {2}^{x} = 4 \)且\( y = 1 \)。
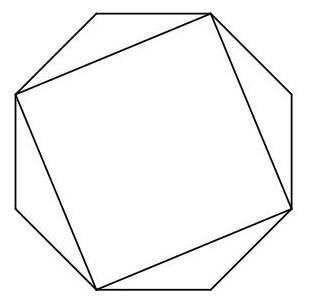
八边形的面积是多少?
设\( O \)为正八边形的中心,\( P, Q \)和\( R \)为八边形相邻的两个顶点,如右图所示。设\( K \)为\( {OQ} \)与\( {PR} \)的交点。
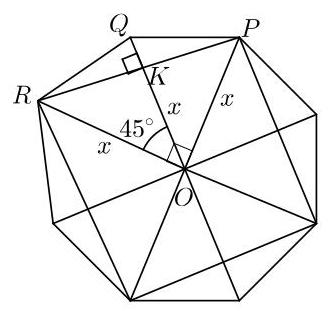
设\( x \)为\( O \)到八边形各顶点的距离。
由于正方形的边长为\( 1,{PR} = 1 \)。对直角三角形\( {PRO} \)应用勾股定理,得\( {x}^{2} + {x}^{2} = {1}^{2} \)。因此\( {x}^{2} = \frac{1}{2} \),从而\( x = \frac{1}{\sqrt{2}} \)。
三角形\( {ROQ} \)的底边\( {OQ} \)长度为\( x \),即\( \frac{1}{\sqrt{2}} \),高为\( {RK} \),长度为\( \frac{1}{2} \)。因此三角形\( {ROQ} \)的面积为\( \frac{1}{2} \times \frac{1}{\sqrt{2}} \times \frac{1}{2} \),等于\( \frac{1}{4\sqrt{2}} \)。
八边形由8个全等于三角形\( {ROQ} \)的三角形组成。
因此八边形的面积为\( 8 \times \frac{1}{4\sqrt{2}} = \sqrt{2} \)。
供探究
\[ \text{area} = \frac{1}{2}\text{(base} \times \text{height).} \]
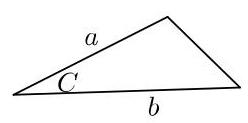
(b) 你的论证是否同时涵盖\( C \)为钝角和锐角的情形?
下列哪一个是反射后抛物线的方程?
解答
方法1
方程为\( y = {x}^{2} \)的抛物线与方程为\( y = x + 2 \)的直线相交于满足\( {x}^{2} = x + 2 \)的点。该方程可整理为\( {x}^{2} - x - 2 = 0 \),再因式分解为\( \left( {x + 1}\right) \left( {x - 2}\right) = 0 \),故其解为-1和2。当\( x = - 1 \)时,有\( y = 1 \);当\( x = 2 \)时,有\( y = 4 \)。因此抛物线与直线交于坐标为(-1,1)和(2,4)的两点,如右图所示。
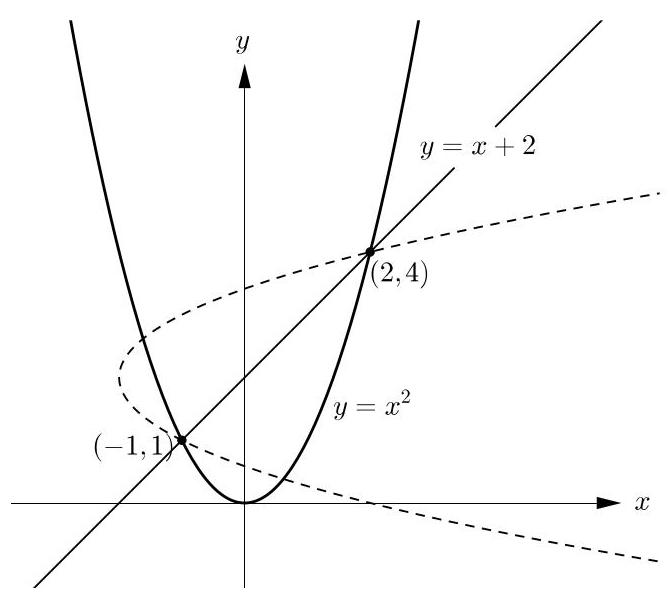
这两点关于该直线反射后位置不变,因此反射后的抛物线也经过这两点。
现在可逐一检验给出的选项方程,看其是否为经过点(-1,1)和(2,4)的曲线方程。
例如,由于\( - 1 \neq {1}^{2} + 4 \times 1 + 2 \),点(-1,1)的坐标不满足方程\( x = {y}^{2} + {4y} + 2 \),因此\( x = {y}^{2} + {4y} + 2 \)不是经过(-1,1)的曲线方程,从而也不是反射后抛物线的方程。
由于\( - 1 = {1}^{2} - 4 \times 1 + 2 \)且\( 2 = {4}^{2} - 4 \times 4 + 2 \),可知点(-1,1)和(2,4)均位于方程为\( x = {y}^{2} - {4y} + 2 \)的曲线上。经验证,这两点不在其他任何方程所表示的曲线上。
因此,在SMC(Senior Mathematics Challenge,高级数学竞赛)的背景下,我们可以得出反射抛物线的方程为\( x = {y}^{2} - {4y} + 2 \)。
如果选项中没有给出方程,我们就需要计算反射抛物线的方程。第二种方法采用了这一思路。
方法二
我们留给读者自行验证:当坐标为(x, y)的点\( P \)关于方程为\( y = x + 2 \)的直线反射时,其像点的坐标为。
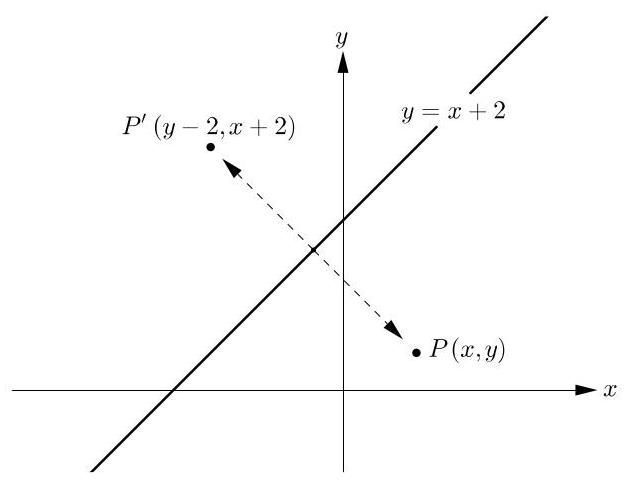
我们令\( {x}^{\prime } = y - 2 \)和\( {y}^{\prime } = x + 2 \),于是
\[ x = {y}^{\prime } - 2\text{ and }y = {x}^{\prime } + 2 \]
坐标为\( \left( {{x}^{\prime },{y}^{\prime }}\right) \)的点位于抛物线反射后的像上当且仅当点(x, y)位于原抛物线上,即当且仅当\( y = {x}^{2} \)。因此,点\( \left( {{x}^{\prime },{y}^{\prime }}\right) \)位于抛物线像上的条件由方程\( \left( {{x}^{\prime } + 2}\right) = {\left( {y}^{\prime } - 2\right) }^{2} \)给出。
展开后,该方程可写为\( {x}^{\prime } + 2 = {y}^{\prime 2} - 4{y}^{\prime } + 4 \)。整理此方程并去掉撇号,我们推得反射抛物线的方程为
\[ x = {y}^{2} - {4y} + 2 \]
探究题
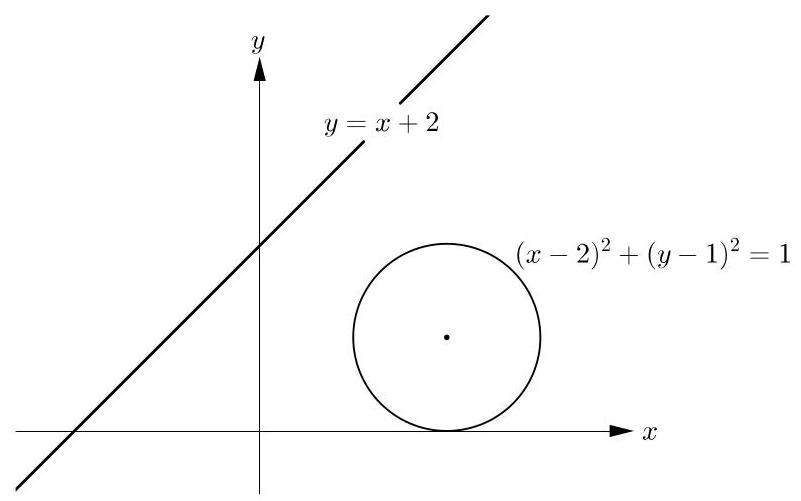
求圆心在(2,1)、半径为1的圆关于方程为\( y = x + 2 \)的直线反射后所得圆的方程。
[注意:圆心在(2,1)、半径为1的圆的方程为\( {\left( x - 2\right) }^{2} + {\left( y - 1\right) }^{2} = 1 \)。]
本题中,为方便起见,我们把一条直线视为与其自身平行。
设给定集合中共有\( l \)条直线。每条直线与该集合中除与其平行的直线外的所有直线相交。因此,由于集合中每条直线与10条直线相交,故每条直线与\( l - {10} \)条直线平行。我们令\( k = l - {10} \)。
那么\( l = {nk} \),其中\( n \)为某个正整数。该集合中的\( {nk} \)条直线构成\( n \)个子集,每个子集包含\( k \)条互相平行的直线,且不同子集中的直线互不平行。
每条直线与其余\( {nk} \)条直线中的\( k \)条不相交,因此每条直线与\( {nk} - k \)条直线相交,即与\( \left( {n - 1}\right) k \)条直线相交。
已知\( \left( {n - 1}\right) k = {10} \)。因此\( n - 1 \)和\( k \)是乘积为10的正整数。下表列出了所有乘积为10的\( n - 1 \)和\( k \)的可能组合。第三列和第四列分别给出对应的\( n \)和\( {nk} \)的值,后者为该集合中直线的总数。
| \( n - 1 \) | \( k \) | \( n \) | \( {nk} \) |
| 1 | 10 | 2 | 20 |
| 2 | 5 | 3 | 15 |
| 5 | 2 | 6 | 12 |
| 10 | 1 | 11 | 11 |
由该表可见,在“每条直线与其余10条直线相交”的直线集合中,直线数量只可能是11、12、15或20。特别地,16不可能是该集合中的直线数量。
供探究
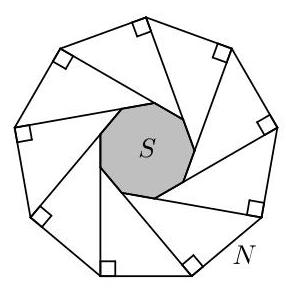
\( S \)的面积占\( N \)面积的几分之几?
设较大正九边形\( N \)的边长为\( x \),较小正九边形\( S \)的边长为\( y \)。由于\( S \)与\( N \)为相似图形,其面积之比为\( {y}^{2} : {x}^{2} \)。因此,用\( N \)的面积表示\( S \)的面积,所求分数为\( \frac{{y}^{2}}{{x}^{2}} \)。
两九边形之间的区域被分成九个三角形。其中相邻的两个三角形\( {JKL} \)和\( {PLM} \)如右图所示。
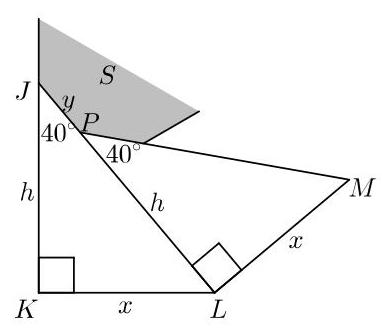
三角形\( {JKL} \)和\( {PLM} \)分别在\( K \)和\( L \)处为直角。边\( {KL} \)和\( {LM} \)的长度均为\( x \),因为它们都是正九边形\( N \)的边。这些三角形中位于\( J \)和\( P \)处的角是\( S \)的外角,因此它们均为\( \frac{1}{9} \times {360}^{ \circ } \),即\( {40}^{ \circ } \)。
在直角三角形\( {JKL} \)和\( {PLM} \)中,对应角相等且\( {KL} = {LM} \)。因此这两个三角形全等,从而\( {JK} = {PL} \)。设\( h \)为\( {JK} \)和\( {PL} \)的共同长度。
在直角三角形\( {JKL} \)中,斜边\( {JL} \)的长度为\( y + h \)。对该三角形应用勾股定理,得\( {x}^{2} + {h}^{2} = {\left( y + h\right) }^{2} \)。展开后得到\( {x}^{2} + {h}^{2} = {y}^{2} + {2yh} + {h}^{2} \),因此\( {x}^{2} = {y}^{2} + {2hy} \)。于是\( \frac{{x}^{2}}{{y}^{2}} = \frac{y + {2h}}{y} \),从而
\[ \frac{{y}^{2}}{{x}^{2}} = \frac{y}{y + {2h}} \tag{1} \]
由三角形\( {JKL} \)可得\( \frac{h}{y + h} = \cos {40}^{ \circ } \),因此\( y + h = \frac{h}{\cos {40}^{ \circ }} \),从而
\[ y = \frac{h}{\cos {40}^{ \circ }} - h\;\text{ and }\;y + {2h} = \frac{h}{\cos {40}^{ \circ }} + h. \tag{2} \]
将(2)代入方程(1)右侧,即可推出\( S \)的面积与\( N \)的面积之比为
\[ \frac{{y}^{2}}{{x}^{2}} = \frac{\frac{h}{\cos {40}^{ \circ }} - h}{\frac{h}{\cos {40}^{ \circ }} + h} = \frac{h - h\cos {40}^{ \circ }}{h + h\cos {40}^{ \circ }} = \frac{1 - \cos {40}^{ \circ }}{1 + \cos {40}^{ \circ }}. \]