1.
下列数字中有一个是质数,它是哪一个?
A \( {2017} - 2 \) B \( {2017} - 1 \) C 2017 D \( {2017} + 1 \) E \( {2017} + 2 \)
2.
去年,一条来自维根(Wigan)名叫戴夫(Dave)的蚯蚓以英国发现的最大蚯蚓身份载入纪录。戴夫长\( {40}\mathrm{\;{cm}} \),质量为\( {26}\mathrm{\;g} \)。它的单位长度质量是多少?
A \( {0.6}\mathrm{\;g}/\mathrm{{cm}} \) B \( {0.65}\mathrm{\;g}/\mathrm{{cm}} \) C \( {0.75}\mathrm{\;g}/\mathrm{{cm}} \) D \( {1.6}\mathrm{\;g}/\mathrm{{cm}} \) E \( {1.75}\mathrm{\;g}/\mathrm{{cm}} \)
3.
将五个整数2,5,6,9,14重新排列。在新排列中,前三个整数之和等于后三个整数之和。新排列中的中间数是多少?
A 2 B 5 C 6 D 9 E 14
4.
下列哪一项等于\( {2017} - \frac{1}{2017} \)?
A \( \frac{{2017}^{2}}{2016} \) B \( \frac{2016}{2017} \) C \( \frac{2018}{2017} \) D \( \frac{4059}{2017} \) E \( \frac{{2018} \times {2016}}{2017} \)
5.
一光年约等于\( 6 \times {10}^{12} \)英里。2016年,哈勃太空望远镜创下新的宇宙观测纪录,观测到距离134亿光年的星系。这大约是多少英里?
\( A\;8 \times {10}^{20} \) \( \mathrm{B}8 \times {10}^{21} \) C \( 8 \times {10}^{22} \) D \( 8 \times {10}^{23} \) \( \mathrm{E}8 \times {10}^{24} \)
6.
图中的圆需要着色,使得任意两个由线段连接的圆颜色不同。所需的最少颜色数是多少?
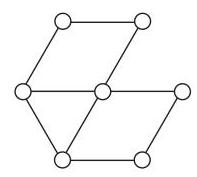
A 2 B 3 C 4 D 5 E 6
7.
正整数\( k \)满足方程\( \sqrt{2} + \sqrt{8} + \sqrt{18} = \sqrt{k} \)。\( k \)的值是多少?
A 28 B 36 C 72 D 128 E 288
8.
计算后,下列哪一项不是整数?
A \( {1}^{-1} \) B \( {4}^{-\frac{1}{2}} \) C \( {6}^{0} \) D \( {8}^{\frac{2}{3}} \) E \( {16}^{\frac{3}{4}} \)
9.
图示为一个\( n \times \left( {n + 1}\right) \)矩形,由\( k \times \left( {k + 1}\right) \)矩形平铺而成,其中\( n \)和\( k \)为整数,且\( k \)取1到8的所有整数值。
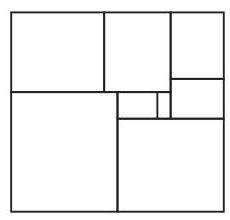
\( n \)的值是多少?
A 16 B 15 C 14 D 13 E 12
10.
一个矩形被分成三个全等的小矩形,如图所示。

每个小矩形都与大矩形相似。
在这四个矩形中,较长边与较短边的长度之比是多少?
A \( 2\sqrt{3} : 1 \) B 3 : 1 C 2 : 1 D \( \sqrt{3} : 1 \) E \( \sqrt{2} : 1 \)
11.
青少年Sam和Jo注意到关于他们年龄的以下事实:他们年龄的平方差等于他们年龄之和的四倍;他们年龄之和等于他们年龄之差的八倍。
两人中年龄较大者的年龄是多少?
A 15 B 16 C 17
D 18 E 19
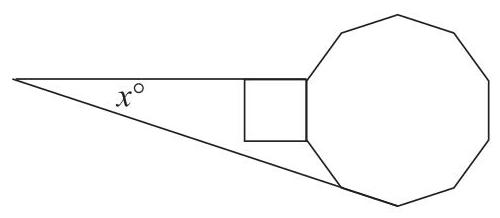
12.
图示为一个正方形和一个正十边形共用一条边。正方形的一条边被延长,与十边形的一条延长边相交。\( x \)的值是多少?
A 15 B 18 C 21 D 24 E 27
13.
Isobel:“Josh是无辜的” Genotan:“Tegan有罪”
Josh:“Genotan有罪” Tegan:“Isobel是无辜的”
只有有罪的人在说谎;其余所有人都在说真话。谁有罪?A Isobel B Josh C Genotan D Tegan E 需要更多信息
14.
在图中,所有标记为\( \bullet \)的角都与标记为\( {x}^{ \circ } \)的角大小相等。
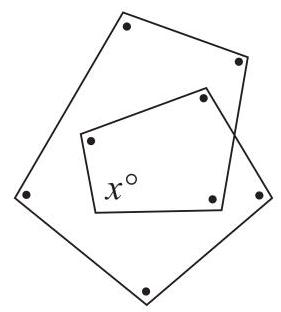
\( x \)的值是多少?
A 100 B 105 C 110 D 115 E 120
15.
图示为一个正方形\( {PQRS} \)。点\( T, U, V \)和\( W \)位于正方形的边上,使得\( {PT} = 1,{QU} = 2,{RV} = 3 \)且\( {SW} = 4 \)。\( {TUVW} \)的面积是\( {PQRS} \)的一半。\( {PQ} \)的长度是多少?
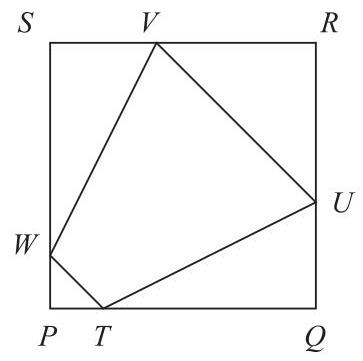
A 5 B 6 C 7 D 8 E 9
16.
图示为一个正方形内有两个直角三角形。较大三角形的两条直角边长度分别为15和20。
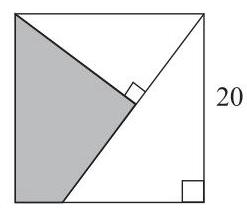
15
阴影四边形的面积是多少?
A 142 B 146 C 150 D 154 E 158
17.
艾米、贝丝和克莱尔各自有一些糖果。艾米把她糖果的三分之一给了贝丝。贝丝把她此时糖果总数的三分之一给了克莱尔。然后克莱尔把她此时糖果总数的三分之一给了艾米。最终三个女孩的糖果数量相同。
克莱尔最初有40颗糖果。贝丝最初有多少颗糖果?
A 20 B 30 C 40 D 50 E 60
18.
任意两个正数\( x \)和\( y \)的算术平均数(arithmetic mean)\( A \)定义为\( A = \frac{1}{2}\left( {x + y}\right) \),它们的几何平均数(geometric mean)\( G \)定义为\( G = \sqrt{xy} \)。对于两个特定值\( x \)和\( y \),且\( x > y \),比值\( A : G = 5 : 4 \)。对于这些\( x \)和\( y \)的值,比值\( x : y \)是多少?
A 5 : 4 B 2 : 1 C 5 : 2 D \( 7 : 2 \) E 4 : 1
19.
图示为一个半径为1的圆与\( 2 \times 4 \)矩形的三条边相切。矩形的一条对角线与圆相交于\( P \)和\( Q \),如图所示。弦\( {PQ} \)的长度是多少?
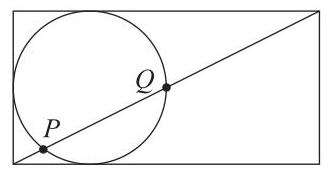
E 2
A ✓\( \overline{5} \) B \( \frac{4}{\sqrt{5}} \) C \( \sqrt{5} - \frac{2}{\sqrt{5}} \) D \( \frac{5\sqrt{5}}{6} \)
20.
图示为一个边长为1的正方形\( {PQRS} \),以及四条弧,每条弧都是四分之一圆。弧\( {TRU} \)的圆心为\( P \);弧\( {VPW} \)的圆心为\( R \);弧\( {UV} \)的圆心为\( S \);弧\( {WT} \)的圆心为\( Q \)。
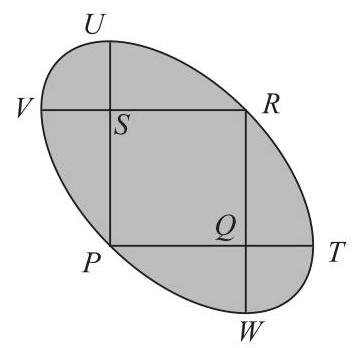
阴影区域的周长是多少?
A 6 B \( \left( {2\sqrt{2} - 1}\right) \pi \) C \( \left( {\sqrt{2} - \frac{1}{2}}\right) \pi \)
D \( {2\pi } \) E \( \left( {3\sqrt{2} - 2}\right) \pi \)
21.
有多少对正整数(x, y)满足方程\( {4}^{x} = {y}^{2} + {15} \)?
A 0 B 1 C 2 D 4 E 无限多
22.
图示为一个正八边形,通过画四条对角线构成一个正方形。正方形的边长为1。
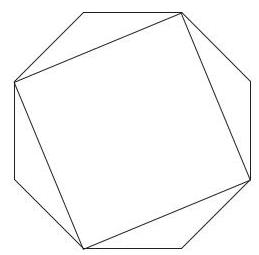
八边形的面积是多少?
A \( \frac{\sqrt{6}}{2} \) B \( \frac{4}{3} \) C \( \frac{7}{5} \) D \( \sqrt{2} \) E \( \frac{3}{2} \)
23.
方程为\( y = {x}^{2} \)的抛物线关于方程为\( y = x + 2 \)的直线作反射。下列哪一个是反射后抛物线的方程?
A \( x = {y}^{2} + {4y} + 2 \) B \( x = {y}^{2} + {4y} - 2 \) C \( x = {y}^{2} - {4y} + 2 \)
D \( x = {y}^{2} - {4y} - 2 \) \( \mathrm{E}x = {y}^{2} + 2 \)
24.
平面上有一组直线,其中每条直线恰好与另外十条直线相交。下列哪一个不可能是该集合中的直线数量?
A 11 B 12 C 15 D 16 E 20
25.
图示为一个正九边形\( N \)。沿\( N \)顺时针方向,在每个顶点处画一条与前一条边垂直的线段,从而得到一个较小的九边形\( S \),图中阴影部分所示。
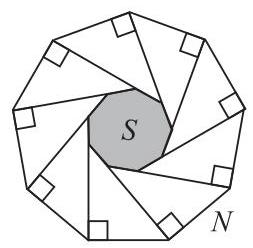
\( S \)的面积占\( N \)面积的几分之几?
A \( \frac{1 - \cos {40}^{ \circ }}{1 + \cos {40}^{ \circ }} \) B B \( \frac{\cos {40}^{ \circ }}{1 + \cos {40}^{ \circ }} \) C \( \frac{\sin {40}^{ \circ }}{1 + \sin {40}^{ \circ }} \) D \( \frac{1 - \sin {40}^{ \circ }}{1 + \sin {40}^{ \circ }} \) E \( \frac{1}{9} \)