SOLUTION
两个奇数相乘,结果仍是奇数。因此,一个奇整数(odd integer)的正整数次幂仍是奇数。同理,一个偶整数(even integer)的正整数次幂仍是偶数。
由此可知,在给定的数中,\( {1}^{2},{3}^{4} \) 和 \( {5}^{6} \) 是奇数,而 \( {2}^{3} \) 和 \( {4}^{5} \) 是偶数。
因此,给定的表达式中有 3 个求值结果为奇数。
供探究
(a) 能被 3 整除?
(b) 能被 4 整除?
(c) 能被 6 整除?
(d) 能被 12 整除?
SOLUTION
2018 的素因数分解为 \( {2018} = 2 \times {1009} \)。这两个素因数之和为 \( 2 + {1009} = {1011} \)。
注
要验证1009是质数(prime)并没有非常快捷的方法,因为这需要检查所有小于1009的质数都不是其因数。[为什么这样就足够?] 幸运的是,题目告诉我们2018是两个质数的乘积。由此我们可以推断出第二个因数1009是质数。
CD 解答
因为\( {135}^{ \circ } = {90}^{ \circ } + {45}^{ \circ } \),顺时针旋转\( {135}^{ \circ } \)等价于先顺时针旋转(即四分之一圈),再顺时针旋转(即八分之一圈)。
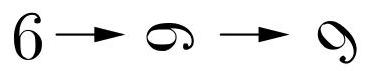
因此,如图所示,顺时针旋转\( {135}^{ \circ } \)后得到的图形对应选项D。
SOLUTION
利用平方差公式分解,我们得到\( {2019}^{2} - {2014}^{2} = \)\( \left( {{2019} - {2014}}\right) \left( {{2019} + {2014}}\right) = 5 \times {4033} \),因此它是5的倍数。
\( {2019}^{2} \times {10}^{2} \)是\( {10}^{2} \)的倍数,也就是100的倍数,因此也是5的倍数。
\( {2020}^{2} \div {101}^{2} = {\left( {20} \times {101}\right) }^{2} \div {101}^{2} = {20}^{2} = {400} \),所以它是5的倍数。
因为\( {2010}^{2} \)和\( {2005}^{2} \)都是5的倍数,它们的差\( {2010}^{2} - {2005}^{2} \)也是5的倍数。
然而,\( {2015}^{2} \div {5}^{2} = {\left( \frac{2015}{5}\right) }^{2} = {403}^{2} \),而403不是\( 5,{403}^{2} \)的倍数,因此\( {2015}^{2} \div {5}^{2} = {\left( \frac{2015}{5}\right) }^{2} = {403}^{2} \)不是5的倍数。
因此正确答案是选项\( \mathrm{E} \)。
供探究
(a) 对于所有正整数\( m \)和\( n \),若\( m \)和\( n \)都是5的倍数,则\( m - n \)也是5的倍数。
(b) 对于所有正整数\( m \),若\( m \)不是5的倍数,则\( {m}^{2} \)也不是5的倍数。
解答
评注
在限定时间内,若不使用计算器,无法通过将这些分数计算到足够多位小数来回答此题。
同样,也不应仅凭以下事实来判断例如\( \frac{397}{101} \)与\( \frac{487}{121} \)的相对大小:
\[ \frac{397}{101} < \frac{487}{121} \Leftrightarrow {397} \times {121} < {487} \times {101}. \]
相反,最佳方法是注意到这五个分数都接近4,然后判断哪些小于4,哪些大于4。
我们注意到
\[ \frac{397}{101} < \frac{404}{101} = 4 \]
\[ \frac{487}{121} > \frac{484}{121} = 4 \]
\[ \frac{596}{153} < \frac{612}{153} = 4 \]
\[ \frac{678}{173} < \frac{692}{173} = 4 \]
并且
\[ \frac{796}{203} < \frac{812}{203} = 4 \]
这些计算表明,选项\( \mathrm{B} \)给出的分数是唯一大于4的,因此它是给定数中最大的。
供探究
\[ \frac{527}{105},\frac{617}{123},\frac{707}{141},\frac{803}{161},\frac{917}{183}\text{.} \]
解答
评注
我们最不想做的就是先算出 \( {25} \times {15} \times 9 \times {5.4} \times {3.24} \) 的值,再对其结果进行因数分解。
相反,我们把小数写成分数,再对各个数进行因数分解,然后约分。
我们有 \( {25} = {5}^{2},{15} = 3 \times 5,9 = {3}^{2},{5.4} = \frac{54}{10} = \frac{27}{5} = \frac{{3}^{3}}{5} \) 和 \( {3.24} = \frac{324}{100} = \frac{81}{25} = \frac{{3}^{4}}{{5}^{2}} \)。因此,
\[ {25} \times {15} \times 9 \times {5.4} \times {3.24} = {5}^{2} \times \left( {3 \times 5}\right) \times {3}^{2} \times \frac{{3}^{3}}{5} \times \frac{{3}^{4}}{{5}^{2}}. \]
现在可以在分子和分母中约去因子 \( {5}^{2} \) 和 5,从而得出
\[ {25} \times {15} \times 9 \times {5.4} \times {3.24} = 3 \times {3}^{2} \times {3}^{3} \times {3}^{4} \]
\[ = {3}^{10}\text{.} \]
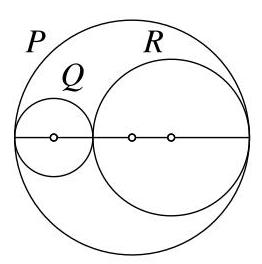
\( \frac{\text{ circumference of }Q + \text{ circumference of }R}{\text{ circumference of }P} \) 的值是多少?
SOLUTION
设圆 \( Q \) 的半径为 \( q \),圆 \( R \) 的半径为 \( r \)。我们看到圆 \( P \) 的直径为 \( {2q} + {2r} \),因此 \( P \) 的半径为 \( q + r \)。
现在我们使用公式
\[ \text{circumference} = {2\pi } \times \text{radius,} \]
推导出
\[ \frac{\text{ circumference of }Q + \text{ circumference of }R}{\text{ circumference of }P} = \frac{{2\pi q} + {2\pi r}}{{2\pi }\left( {q + r}\right) } \]
\[ = \frac{{2\pi }\left( {q + r}\right) }{{2\pi }\left( {q + r}\right) } \]
\[ = 1 \]
解答
评注
显然,我们无法通过完全计算\( {7}^{2018} \)再查看其最后两位数字来回答这个问题。
相反,我们利用一个事实:乘积\( a \times b \)的最后两位仅由\( a \)和\( b \)的最后两位决定,然后寻找规律。
为方便表示一个整数的最后两位,我们引入一种记号。对此尚无标准记号(见下文8.1)。为回答本题,我们用\( \left\lbrack n\right\rbrack \)表示整数\( n \)的最后两位组成的数。例如,[12345]=45。
利用这一记号,可将我们使用的事实写成等式
\[ \left\lbrack {m \times n}\right\rbrack = \left\lbrack {\left\lbrack m\right\rbrack \times \left\lbrack n\right\rbrack }\right\rbrack \]
于是我们有
\[ \left\lbrack {7}^{1}\right\rbrack = \left\lbrack 7\right\rbrack = {07} \]
\[ \left\lbrack {7}^{2}\right\rbrack = \left\lbrack {49}\right\rbrack = {49} \]
\[ \left\lbrack {7}^{3}\right\rbrack = \left\lbrack {{7}^{2} \times 7}\right\rbrack = \left\lbrack {\left\lbrack {7}^{2}\right\rbrack \times \left\lbrack 7\right\rbrack }\right\rbrack = \left\lbrack {{49} \times 7}\right\rbrack = \left\lbrack {343}\right\rbrack = {43} \]
\[ \left\lbrack {7}^{4}\right\rbrack = \left\lbrack {{7}^{3} \times 7}\right\rbrack = \left\lbrack {\left\lbrack {7}^{3}\right\rbrack \times \left\lbrack 7\right\rbrack }\right\rbrack = \left\lbrack {{43} \times 7}\right\rbrack = \left\lbrack {301}\right\rbrack = {01} \]
\[ \left\lbrack {7}^{5}\right\rbrack = \left\lbrack {{7}^{4} \times 7}\right\rbrack = \left\lbrack {\left\lbrack {7}^{4}\right\rbrack \times \left\lbrack 7\right\rbrack }\right\rbrack = \left\lbrack {{01} \times 7}\right\rbrack = \left\lbrack 7\right\rbrack = {07}. \]
给出\( {7}^{n} \)最后两位的序列中,每一项仅取决于前一项。因此,当07再次出现时,可推断由\( \left\lbrack {7}^{n}\right\rbrack \)的值构成的序列是一个长度为4的循环,即
\[ {07},{49},{43},{01},{07},{49},{43},{01},\ldots \]
因为2018\( = {504} \times 4 + 2 \),所以\( \left\lbrack {7}^{2018}\right\rbrack \)是该循环中的第二对数字,即49。
供探究
注
数\( \left\lbrack m\right\rbrack \)是\( m \)除以100的余数。若你熟悉模运算的语言,就会看到\( \left\lbrack m\right\rbrack \equiv m\left( {\;\operatorname{mod}\;{100}}\right) \)。
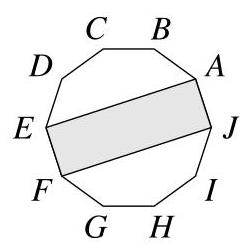
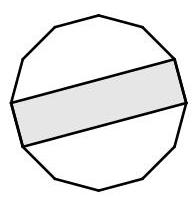
矩形面积与十边形面积之比是多少?
设\( O \)为正十边形(regular decagon)的中心。十边形被从\( O \)到各顶点的半径分割成十个全等的等腰三角形。三角形\( {AOJ} \)和\( {EOF} \)是这十个全等三角形中的两个。
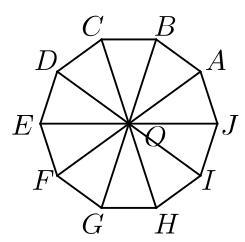
因为\( O \)是矩形\( {AEFJ} \)的中心,且矩形的对角线将其面积分成四个相等的部分,所以三角形\( {EOA} \)和\( {FOJ} \)的面积分别与三角形\( {AOJ} \)和\( {EOF} \)的面积相等。
因此,\( {AEFJ} \)的面积等于构成十边形的十个全等三角形中四个的面积。

故\( {AEFJ} \)的面积与十边形\( {ABCDEFGHI} \)的面积之比为4 : 10,化简后为2 : 5。
供探究
(a) 十边形有一个中心,即存在一个圆通过其所有顶点。(该圆的圆心即为十边形的中心。)
(b) 正十边形的中心也是矩形\( {AEFJ} \)的中心。
(c) 三角形\( {EOA} \)的面积与三角形\( {AOJ} \)的面积相等。
矩形面积与十二边形面积之比是多少?

正方形面积与十二边形面积之比是多少?
她整个骑行的平均速度是多少?
SOLUTION
为了确定Laura整个骑行的平均速度,我们计算她行驶的总距离以及所用的总时间。
因为5分钟是\( \frac{1}{12} \)小时,所以当Laura以\( {12}\mathrm{\;{km}}/\mathrm{h} \)的速度骑行5分钟时,她行驶了\( \frac{1}{12} \times {12}\mathrm{\;{km}} = 1\mathrm{\;{km}} \)。
因为10分钟是\( \frac{1}{6} \)小时,所以当Laura以\( {15}\mathrm{\;{km}}/\mathrm{h} \)的速度骑行10分钟时,她行驶了\( \frac{1}{6} \times {15}\mathrm{\;{km}} = {2.5}\mathrm{\;{km}} \)。
因为15分钟是\( \frac{1}{4} \)小时,所以当Laura以\( {18}\mathrm{\;{km}}/\mathrm{h} \)的速度骑行15分钟时,她行驶了\( \frac{1}{4} \times {18}\mathrm{\;{km}} = {4.5}\mathrm{\;{km}} \)。
因此,Laura在\( 5 + {10} + {15} \)分钟内总共行驶了\( 1\mathrm{\;{km}} + {2.5}\mathrm{\;{km}} + {4.5}\mathrm{\;{km}} = 8\mathrm{\;{km}} \),即30分钟,也就是半小时。
因为Laura在半小时内行驶了\( 8\mathrm{\;{km}} \),所以她的平均速度是\( {16}\mathrm{\;{km}}/\mathrm{h} \)。供探究
\[ y = {x}^{4} + 1\;y = {x}^{4} + x\;y = {x}^{4} + {x}^{2}\;y = {x}^{4} + {x}^{3} \]
原点的坐标为(0,0)。因此它是\( x = 0 \)和\( y = 0 \)的点。由此可知,如果一个方程在\( x = 0 \)时\( y = 0 \),则该方程的图像经过原点。
现在,当\( x = 0 \)时,\( {x}^{4} + 1,{x}^{4} + x,{x}^{4} + {x}^{2} \)和\( {x}^{4} + {x}^{3} \)的值分别为1、0、0和0。因此,在给定的方程中,\( y = {x}^{4} + 1 \)是唯一一个图像不经过原点的方程。
供探究
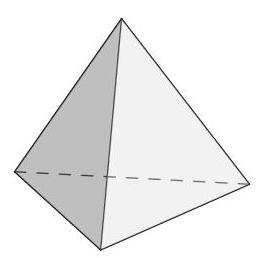
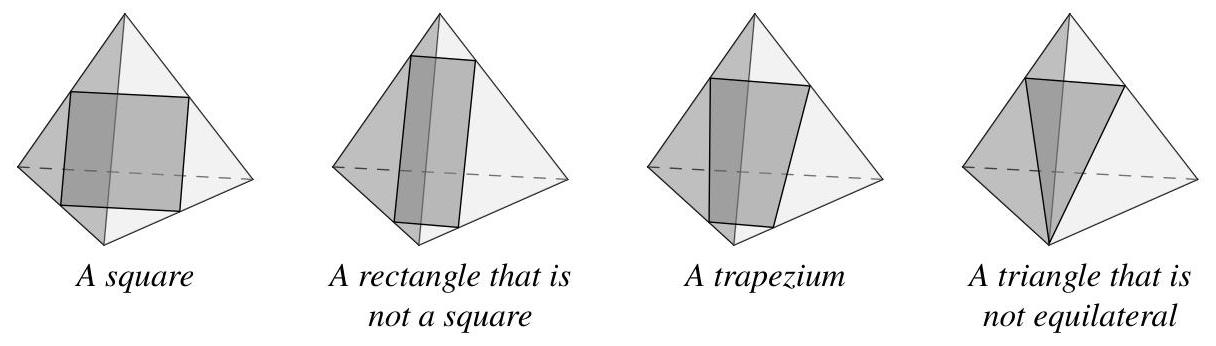
以下哪种形状不可能是该切割所形成的截面形状?
解答
当正四面体被一个单一平面切割时,其四个面每个最多被切割一次。每个面被切割的位置成为新形成截面的边。因此,具有五条边的五边形无法形成。
然而,其余四个选项都是可能的,如下图所示。
当\( P \)的坐标也是正整数时,所有正整数\( m \)的和是多少?A 3 B 5 C 7 D 8 E 10
解答
在点\( P \)处,我们同时有\( y = x \)和\( y = {mx} - 4 \)。因此在\( P \)处我们得到\( x = {mx} - 4 \),从而\( 4 = {mx} - x \)。最后一个等式可写为\( 4 = \left( {m - 1}\right) x \)。若\( m \)和\( x \)均为满足该等式的正整数,则\( m - 1 \)和\( x \)均为4的正整数因子。
因此\( m - 1 \)的可能取值为1、2、4,对应的\( m \)分别为2、3、5,\( x \)和\( y \)分别为4、2、1。
因此,当\( P \)的坐标为正整数时,\( m \)的所有正整数值之和为\( 2 + 3 + 5 = {10} \)。
\[ 1, x, x, x, y, y, y, y, y,8,9,{11}\text{.} \]
这十二个整数的平均数为7,则中位数是多少?
解答
由于给定整数的平均数为7,我们有
\[ 1 + x + x + x + y + y + y + y + y + 8 + 9 + {11} = {12} \times 7. \]
可将最后一个等式改写为\( 1 + {3x} + {5y} + {28} = {84} \),因此\( {3x} + {5y} = {55} \)。
于是\( {3x} = {55} - {5y} = 5\left( {{11} - y}\right) \)。因此,由于\( x \)和\( y \)为整数,\( {3x} \)是5的倍数,从而\( x \)也是5的倍数。
由于这些整数按升序排列,\( 1 \leq x \leq 8 \)。于是\( x = 5 \),因此\( {15} + {5y} = {55} \)。于是\( {5y} = {40} \),从而\( y = 8 \)。
因此,这十二个整数按升序排列为1,5,5,5,8,8,8,8,8,8,9,11。可见中位数为8。
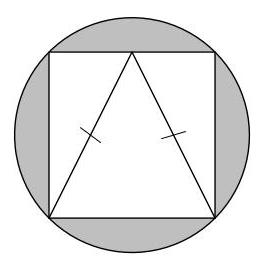
该三角形面积与阴影区域面积之比是多少?
解答
设正方形的边长为\( s \)。由图可知,根据勾股定理(Pythagoras’ theorem),\( {s}^{2} = {1}^{2} + {1}^{2} \),因此\( s = \sqrt{2} \)。
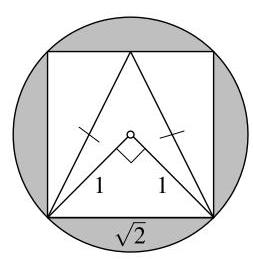
圆的面积为\( \pi \times {1}^{2} \),等于\( \pi \)。正方形的面积为\( \sqrt{2} \times \sqrt{2} \),等于2。因此阴影区域的面积为\( \pi - 2 \)。
等腰三角形的底边为正方形的一条边,长度为\( \sqrt{2} \);其高也为\( \sqrt{2} \)。因此三角形面积为\( \frac{1}{2}\left( {\sqrt{2} \times \sqrt{2}}\right) \),等于1。
于是三角形面积与阴影区域面积之比为\( 1 : \pi - 2 \)。
探究
\[ p + {2q} + {3r} + {4s} = k\;{4p} = {3q} = {2r} = s. \]
求使\( p, q, r \)和\( s \)均为正整数时,\( k \)的最小值。
由方程组\( {4p} = {3q} = {2r} = s \)可得\( q = \frac{4}{3}p, r = {2p} \)和\( s = {4p} \)。
要求\( p \)和\( q \)为正整数,故由方程\( q = \frac{4}{3}p \)可知\( p \)必须是3的倍数。同时注意到,若\( p \)为正整数,则\( r \)和\( s \)亦为正整数。
由此可得
\[ k = p + {2q} + {3r} + {4s} = p + 2\left( {\frac{4}{3}p}\right) + 3\left( {2p}\right) + 4\left( {4p}\right) \]
\[ = p + \frac{8}{3}p + {6p} + {16p} = \frac{77}{3}p. \]
因\( p \)为正整数且为3的倍数,其最小值为3,故\( k \)的最小值为\( \frac{77}{3} \times 3 \),即77。
以下哪个不可能是钱包中硬币的总数?
SOLUTION
我们假设贝萨妮拥有的\( {20}\mathrm{p} \)硬币和\( {50}\mathrm{p} \)硬币的数量分别为\( m \)和\( n \)。(注意\( m \)和\( n \)均为正整数。)
于是贝萨妮共有\( c \)枚硬币,其中\( c = {11} + m + n \)。这些硬币的总面值为\( {11} + {0.20m} + {0.50n} \)英镑,即\( {1100} + {20m} + {50n} \)便士。
由于贝萨妮硬币的平均面值为52便士,\( \frac{{1100} + {20m} + {50n}}{{11} + m + n} = {52} \)。由此可得\( {1100} + {20m} + {50n} = {52}\left( {{11} + m + n}\right) \),进而\( {1100} + {20m} + {50n} = {572} + {52m} + {52n} \)。该方程可整理为\( {2n} = {528} - {32m} \),化简后得\( n = {264} - {16m} \)。
由此可知\( c = {11} + m + n = {11} + m + \left( {{264} - {16m}}\right) = {275} - {15m} \)。因此\( {275} - c = {15m} \)。于是\( {275} - c \)是15的整数倍。
我们现在逐一考虑题目选项给出的\( c \)的不同取值。
我们有\( {275} - {35} = {240} = {15} \times {16},{275} - {50} = {225} = {15} \times {15},{275} - {65} = {210} = {15} \times {14} \)和\( {275} - {95} = {180} = {15} \times {12} \)。因此贝萨妮的钱包里可能有35、50、65或95枚硬币。
然而\( {275} - {40} = {235} \)不是15的整数倍,因此贝萨妮的钱包里不可能有40枚硬币。
以下哪一项是\( P + Q + R \)所有可能取值的完整列表?
我们假设该三角形的实际角为\( {P}^{\prime },{Q}^{\prime } \)和\( {R}^{\prime } \),它们分别被四舍五入为\( P, Q \)和\( R \)。
三角形内角和为\( {180}^{ \circ } \),因此
\[ {P}^{\prime } + {Q}^{\prime } + {R}^{\prime } = {180}^{ \circ }. \]
当一个角向上四舍五入到最接近的度数时,最多增加\( {0.5}^{ \circ } \);向下四舍五入时,最多减少\( {0.5}^{ \circ } \)。因此,
\[ {P}^{\prime } - {0.5}^{ \circ } \leq P \leq {P}^{\prime } + {0.5}^{ \circ }\text{,} \]
\[ {Q}^{\prime } - {0.5}^{ \circ } \leq Q \leq {Q}^{\prime } + {0.5}^{ \circ }\text{,} \]
\[ \text{and}{R}^{\prime } - {0.5}^{ \circ } \leq R \leq {R}^{\prime } + {0.5}^{ \circ }\text{.} \]
将上述不等式相加可得
\[ {P}^{\prime } + {Q}^{\prime } + {R}^{\prime } - {1.5}^{ \circ } \leq P + Q + R \leq {P}^{\prime } + {Q}^{\prime } + {R}^{\prime } + {1.5}^{ \circ }. \]
因此,作为\( {P}^{\prime } + {Q}^{\prime } + {R}^{\prime } = {180}^{ \circ } \),
\[ {178.5}^{ \circ } \leq P + Q + R \leq {181.5}^{ \circ }\text{.} \]
\( P, Q \)和\( R \)均为整数度数,故\( P + Q + R \)亦为整数度数。由此可知,\( P + Q + R \)的唯一可能取值为\( {179}^{ \circ },{180}^{ \circ } \)和\( {181}^{ \circ } \)。
为完成解答,我们证明这些可能取值确实可在某三角形中实现,以下示例予以说明。
\( {P}^{\prime } = {60.3}^{ \circ },{Q}^{\prime } = {60.3}^{ \circ },{R}^{\prime } = {59.4}^{ \circ } \)给出\( P = {60}^{ \circ }, Q = {60}^{ \circ }, R = {59}^{ \circ } \),故\( P + Q + R = {179}^{ \circ } \)。
\( {P}^{\prime } = {60}^{ \circ },{Q}^{\prime } = {60}^{ \circ },{R}^{\prime } = {60}^{ \circ } \)给出\( P = {60}^{ \circ }, Q = {60}^{ \circ }, R = {60}^{ \circ } \),故\( P + Q + R = {180}^{ \circ } \)。
\( {P}^{\prime } = {59.7}^{ \circ },{Q}^{\prime } = {59.7}^{ \circ },{R}^{\prime } = {60.6}^{ \circ } \)给出\( P = {60}^{ \circ }, Q = {60}^{ \circ }, R = {61}^{ \circ } \),故\( P + Q + R = {181}^{ \circ } \)。
我们推断\( {179}^{ \circ },{180}^{ \circ },{181}^{ \circ } \)即为\( P + Q + R \)所有可能取值的完整列表。供探究
“一个正\( m \)边形的外角大小为\( {n}^{ \circ } \),且一个正\( n \)边形的外角大小为\( {m}^{ \circ } \)。”
解答
首先注意多边形至少有3条边,因此只需考虑\( m \geq 3 \)和\( n \geq 3 \)的情形。
正\( m \)边形的外角为\( {\left( \frac{360}{m}\right) }^{ \circ } \)。因此,正\( m \)边形具有外角\( {n}^{ \circ } \)的条件是\( n = \frac{360}{m} \)。该条件可改写为\( {mn} = {360} \)。
同样,这是正\( n \)边形外角为\( {m}^{ \circ } \)的条件。
因此,当且仅当\( m \)和\( n \)均不小于3且\( {mn} = {360} \)时,数对(m, n)满足题设条件。
将360表示为两个均不小于3的正整数之积共有10种方式,它们是
\[ 3 \times {120},4 \times {90},5 \times {72},6 \times {60},8 \times {45},9 \times {40},{10} \times {36},{12} \times {30},{15} \times {24}\text{ and }{18} \times {20}. \]
这10种分解中的每一种都可以按两种顺序排列,从而得到两对满足条件的(m, n)。例如,对应于分解\( 3 \times {120} \),(m, n)可以是(3,120)或(120,3)。
因此共有\( {10} \times 2 \),即20对数(m, n)满足题设条件。供探究
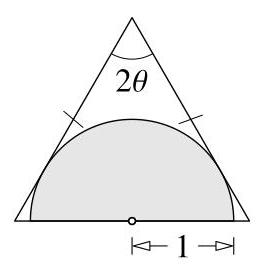
该三角形的面积是多少?
解答
设三角形的顶点为\( P, Q \)和\( R \),其中\( {PQ} = {PR} \),如图所示,并设\( O \)为\( {QR} \)的中点。再设\( T \)为半圆与\( {PR} \)的切点。在三角形\( {PQO} \)和\( {PRO} \)中,我们有\( {PQ} = {PR},{QO} = {RO} \)且边\( {PO} \)公共,因此这两个三角形全等(SSS)。于是三角形\( {PQR} \)的面积是三角形\( {POR} \)面积的两倍。
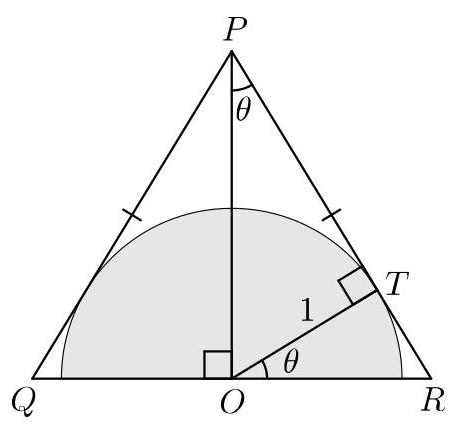
还可推出\( \angle {QPO} = \angle {RPO} = \theta \)。因此\( {PO} \)是\( \angle {QPR} \)的角平分线。于是\( O \)到\( {PQ} \)和\( {PR} \)的距离相等,故\( O \)是半圆的圆心。
我们还可推得\( \angle {POQ} = \angle {POR} = {90}^{ \circ } \)。
\( {OT} \)是半圆的半径,因此长度为1且垂直于切线\( {PR} \)。于是\( {PTO} \)为直角三角形,因此
\[ \frac{OT}{OP} = \sin \theta \]
因此
\[ {OP} = \frac{OT}{\sin \theta } = \frac{1}{\sin \theta }. \]
此外,由三角形\( {POR} \)可得
\[ \frac{OP}{PR} = \cos \theta \]
因此
\[ {PR} = \frac{OP}{\cos \theta } = \frac{1}{\sin \theta \cos \theta .} \]
若将\( {PR} \)视为三角形\( {POR} \)的底边,\( {OT} \)为其底边,则可见
\[ \text{area of}{POR} = \frac{1}{2}\left( {{PR} \times {OT}}\right) = \frac{1}{2\sin \theta \cos \theta }\text{.} \]
于是三角形\( {PQR} \)的面积为\( \frac{1}{\sin \theta \cos \theta } \)。
最终图像的方程是什么?
评注
我们给出两种解答此题的方法。
第一种快捷方法在SMC情境下已足够,因为可假定选项中必有一个正确,且无需给出证明。
第二种方法用代数计算最终图像的方程,是需完整解答时应给出的示例。
方法一
当\( x = 1 \)时,有\( \frac{1}{x} = 1 \),因此坐标为(1,1)的点位于\( y = \frac{1}{x} \)的图像上。
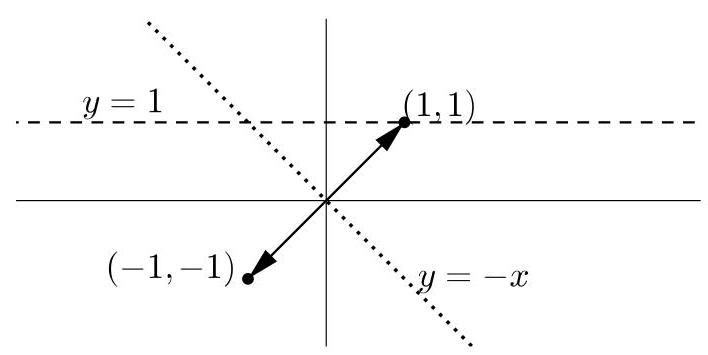
点(1,1)关于直线\( y = 1 \)反射后保持不变,再关于直线\( y = - x \)反射后映射到点(-1,-1)。于是点(-1,-1)位于最终图像上。易验证选项A的方程在\( x = - 1 \)时给出\( y = - 1 \),而其他方程均不具备此性质。因此可排除选项\( \mathrm{B},\mathrm{C},\mathrm{D} \)和\( \mathrm{E} \),从而得出正确选项为\( \mathrm{A} \)。
注
该论证彻底排除了选项B、C、D和E,但并未证明选项\( \mathrm{A} \)的方程就是最终图形的方程,仅表明这是一种可能。
方法二
关于直线\( y = 1 \)的反射将坐标为(x, y)的点与坐标为(x,2-y)的点互换,如右侧第一图所示。
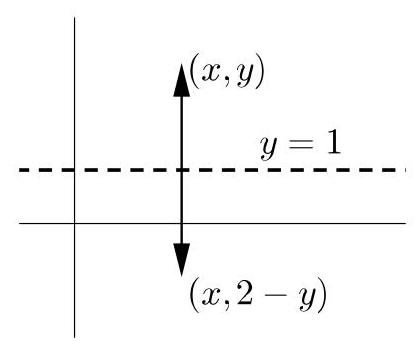
因此,\( y = \frac{1}{x} \)的图形经此反射后的像即为\( 2 - y = \frac{1}{x} \)的图形。
关于直线\( y = - x \)的反射将坐标为(x, y)的点与坐标为(-y,-x)的点互换,如右侧第二图所示。
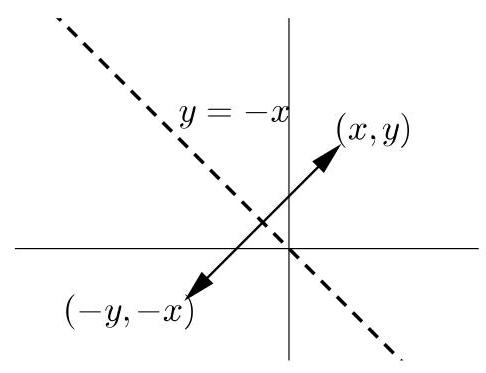
因此,\( 2 - y = \frac{1}{x} \)的图形经此反射后的像即为\( 2 - \left( {-x}\right) = \frac{1}{-y} \)的图形。该方程可整理为\( y = \frac{-1}{\left( x + 2\right) } \)。
供探究
(b) 用几何方法说明:先将\( y = \frac{1}{x} \)的图形关于直线\( y = 1 \)反射,再将所得图形关于直线\( y = - x \)反射,即可得到\( y = \frac{-1}{x + 2} \)的图形。
(b) 设\( f \)为\( x \)的某个函数。证明\( y = f\left( x\right) \)的图形关于直线\( y = 1 \)反射后的像是\( y = 2 - f\left( x\right) \)的图形。
(b) 设\( f \)为\( x \)的某个函数。证明\( y = f\left( x\right) \)的图形关于直线\( y = - x \)反射后的像是一条方程为\( x = - f\left( {-y}\right) \)的曲线。
阴影区域的总面积是多少(位于等腰三角形内部但在等边三角形外部)?
解法
评注
本题可用多种方法解决。我们先给出完整解法,再概述两种其他解法,细节留给读者。你或许还能找到更多方法。
方法1
我们设顶角为\( {120}^{ \circ } \)的等腰三角形的顶点为\( P, Q \)和\( R \),等边三角形的顶点为\( K, L \)和\( M \),如下图所示。
我们还设\( N \)为\( {KM} \)和\( S \)的中点,\( T \)为\( {QR} \)与直线\( {KL} \)和\( {ML} \)的交点。
我们还假设等边三角形\( {KLM} \)的边长为\( {2s} \)
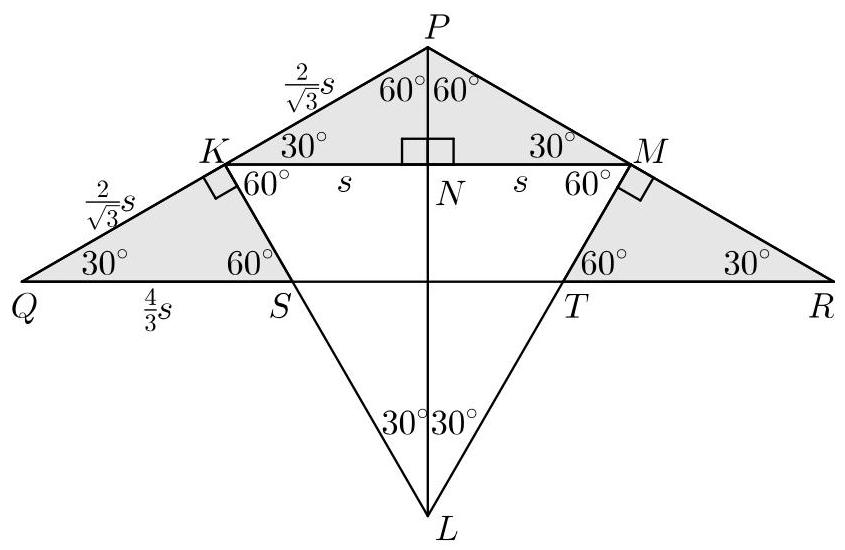
图1
三角形\( {PQR} \)是等腰三角形,且\( {PQ} = {PR} \),\( K \)和\( M \)分别是\( {PQ} \)和\( {PR} \)的中点。因此\( {PK} = {PM} \)。由于\( N \)是\( {KM} \)的中点,我们也有\( {KN} = {NM} \)。因此三角形\( {PKN} \)和\( {PMN} \)的对应边相等,故全等。于是这两个三角形的角分别为\( {90}^{ \circ },{60}^{ \circ } \)和\( {30}^{ \circ } \),如图所示。
同理,三角形\( {KNL} \)和\( {MNL} \)的对应边相等,因此全等。于是它们的角也分别为\( {90}^{ \circ },{60}^{ \circ } \)和\( {30}^{ \circ } \),如图所示。
因为三角形\( {PQR} \)是等腰三角形且\( {PQ} = {PR} \),所以\( \angle {PQR} = \angle {PRQ} \)。因此,由于\( \angle {QPR} = {120}^{ \circ } \)且三角形内角和为\( {180}^{ \circ } \),可得\( \angle {PQR} = \angle {PRQ} = \)\( {30}^{ \circ } \)。
直线\( {PQ} \)在\( K \)处的角之和为\( {180}^{ \circ } \)。因此\( \angle {QKS} = {90}^{ \circ } \)。于是\( {QKS} \)又是一个具有角\( {90}^{ \circ },{60}^{ \circ } \)和\( {30}^{ \circ } \)的三角形。同理,三角形\( {RMT} \)也是如此。因为\( {QK} = {RM} \),所以三角形\( {QKS} \)和\( {RMT} \)全等。
因此我们看到\( {KPN},{QSK} \)和\( {LKN} \)是相似三角形,其角分别为\( {90}^{ \circ },{60}^{ \circ } \)和\( {30}^{ \circ } \)。
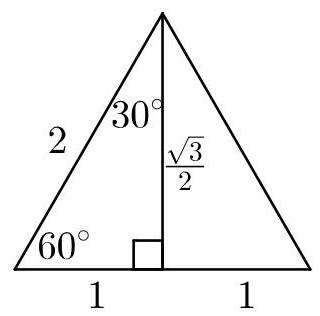
若把具有这些角的三角形视为等边三角形的一半,则在该三角形中,斜边与另外两边的比为\( 2 : \frac{\sqrt{3}}{2} : 1 \)。
因此,作为\( {KN} = s \),可以得出\( {KP} = \frac{2}{\sqrt{3}}s \)。
因此\( {QK} = {KP} = \frac{2}{\sqrt{3}}s \),从而\( {QS} = \frac{2}{\sqrt{3}} \times \frac{2}{\sqrt{3}}s = \frac{4}{3}s \)。
相似三角形的面积之比等于其对应线性尺寸之比的平方。我们已经看到,相似三角形\( {KPN},{QSK} \)和\( {LKN} \)的斜边长度分别为\( \frac{2}{\sqrt{3}}s \)、\( \frac{4}{3}s \)和\( {2s} \)。这些长度之比为\( \frac{2}{\sqrt{3}} : \frac{4}{3} : 2 \),因此这些三角形的面积之比为\( \frac{4}{3} : \frac{16}{9} : 4 \),即\( \frac{1}{3} : \frac{4}{9} : 1 \)。
因此,三角形\( {KPN} \)和\( {QSK} \)的面积分别为三角形\( {LKN} \)面积的\( \frac{1}{3} \)和\( \frac{4}{9} \)。现在\( \frac{1}{3} + \frac{4}{9} = \frac{7}{9} \)。因此,三角形\( {KPN} \)和\( {QSK} \)的面积之和为三角形\( {LKN} \)面积的\( \frac{7}{9} \)。
同样,三角形\( {MPN} \)与\( {TRM} \)的面积之和等于三角形\( {LMN} \)面积的\( \frac{7}{9} \)。
因此,阴影区域的面积是等边三角形面积的\( \frac{7}{9} \)。所以,阴影面积为\( \frac{7}{9} \times {36} = {28} \)。
方法二
设\( O \)为\( {QR} \)的中点,并将\( O \)与\( K, L \)和\( M \)连接。
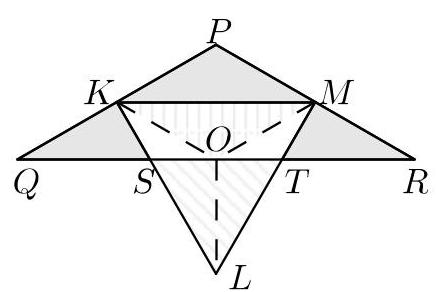
图2
可以验证,三角形\( {PKM},{KOM},{LOK} \)与\( {MOL} \)均全等。因此,三角形\( {PKM} \)的面积是\( {KLM} \)面积的三分之一,从而三角形\( {PKM} \)的面积为12。
还可以证明,\( {ST} \) 的长度是 \( {KM} \) 长度的 \( \frac{2}{3} \)。因此,三角形 \( {LTS} \) 的面积是 \( {KLM} \) 面积的 \( \frac{4}{9} \),即 16。
还可以验证三角形\( {KQS},{MTR},{SLO} \)与\( {LTO} \)全等。
因此,三角形\( {KQS} \)与\( {MTR} \)的面积之和等于三角形\( {STL} \)的面积,即16。
因此,阴影区域的面积为\( {12} + {16} = {28} \)。
方法3
我们给出的第三种解法更具可视化。它依赖于图表的性质,若需完整解答,这些性质还需详细论证。
考虑下图3中的示意图,其中粗线勾勒出的为原始图形,以及它的两个副本,旋转了\( \pm {120}^{ \circ } \)。
这表明图3中的阴影区域等于原始等边三角形面积的三分之一,即12。我们还看到大等边三角形的面积为\( 4 \times {36} = {144} \)。
现在考虑图4,它展示了相同的示意图,并叠加了若干较小的等边三角形。
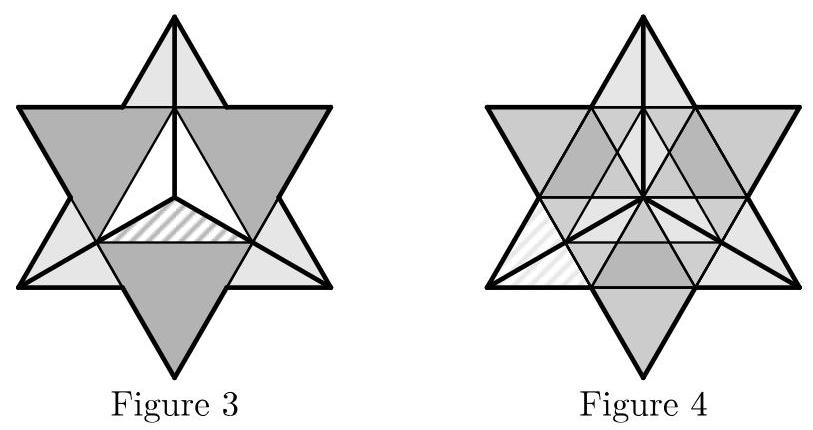
这表明图4中的阴影区域等于大等边三角形面积的九分之一,即16。
因此,原图中的阴影区域为\( {12} + {16} = {28} \)。
供探究
以下哪个公式定义了函数\( g \),使得对所有\( x \)的值,\( g\left( {f\left( x\right) }\right) = x? \)
因为\( f\left( x\right) = {ax} + b \),所以对于所有实数\( x \),
\[ f\left( {f\left( x\right) }\right) = f\left( {{ax} + b}\right) \]
\[ = a\left( {{ax} + b}\right) + b \]
\[ = {a}^{2}x + {ab} + b\text{.} \]
因此,对于所有实数\( x \),
\[ f\left( {f\left( {f\left( x\right) }\right) }\right) = f\left( {{a}^{2}x + {ab} + b}\right) \]
\[ = a\left( {{a}^{2}x + {ab} + b}\right) + b \]
\[ = {a}^{3}x + {a}^{2}b + {ab} + b \]
\[ = {a}^{3}x + \left( {{a}^{2} + a + 1}\right) b \]
因为表达式\( {a}^{3}x + \left( {{a}^{2} + a + 1}\right) b \)和\( {27x} - {52} \)对所有实数\( x \)取值相同,所以它们的系数对应相等。于是\( {a}^{3} = {27} \)且\( \left( {{a}^{2} + a + 1}\right) b = - {52} \)。由此可得\( a = 3 \),进而\( {13b} = - {52} \),从而\( b = - 4 \)。因此函数\( f \)由\( f\left( x\right) = {3x} - 4 \)定义。
评注
我们现在需要求出函数\( g \)的表达式,使得\( g\left( {f\left( x\right) }\right) = x \)。若\( f\left( x\right) = y \),这意味着\( g\left( y\right) = x \)。因此,我们采用的方法是从方程\( y = f\left( x\right) \)出发,然后将其整理成\( x = g\left( y\right) \)的形式。
我们有
\[ y = f\left( x\right) \Leftrightarrow y = {3x} - 4 \]
\[ \Leftrightarrow {3x} = y + 4 \]
\[ \Leftrightarrow x = \frac{1}{3}y + \frac{4}{3}\text{.} \]
于是\( g \)由公式\( g\left( y\right) = \frac{1}{3}y + \frac{4}{3} \)给出。用\( x \)改写此公式得到\( g\left( x\right) = \frac{1}{3}x + \frac{4}{3} \)。
供探究
(a) \( f\left( x\right) = {7x} - {28} \) .
(b) \( f\left( x\right) = \sqrt{x + 3} + 5 \) .
(c) \( f\left( x\right) = \frac{x}{x + 1} \) .
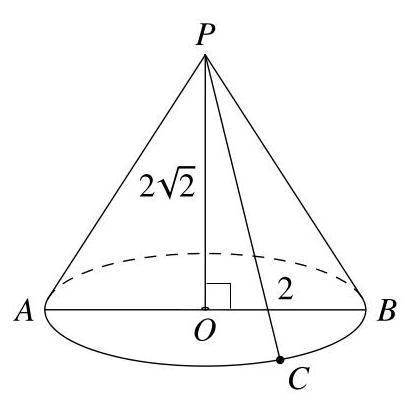
从\( A \)到\( {PC} \)的最短距离是多少?
解答
三角形\( {POA} \)在\( O \)处为直角。因此,根据勾股定理,\( P{A}^{2} = A{O}^{2} + P{O}^{2} = {2}^{2} + {\left( 2\sqrt{2}\right) }^{2} = \)\( 4 + 8 = {12} \)。于是\( {PA} = \sqrt{12} = 2\sqrt{3} \)。同理,\( {PC} = 2\sqrt{3} \)。

由于\( \operatorname{arc}{AC} : \operatorname{arc}{CB} = 2 : 1 \),于是\( \angle {AOC} \):\( \angle {COB} = 2 : 1 \)。因此\( \angle {COB} = {60}^{ \circ } \)。
现在\( {OC} \)和\( {OB} \)的长度均为2,因为它们是以\( O \)为圆心的圆的半径。由于\( \angle {COB} = {60}^{ \circ } \),于是三角形\( {COB} \)为等边三角形。因此\( {BC} = 2 \)。
现在我们将注意力转向三角形\( {ACB} \)。在该三角形中,\( \angle {ACB} = {90}^{ \circ } \),因为它位于半圆中的角,\( {AB} = 4 \)且\( {BC} = 2 \)。因此,根据毕达哥拉斯定理(Pythagoras’ Theorem),\( A{B}^{2} = A{C}^{2} + B{C}^{2} \),从而\( {4}^{2} = A{C}^{2} + {2}^{2} \)。于是\( A{C}^{2} = {4}^{2} - {2}^{2} = {16} - 4 = {12} \)。因此\( {AC} = \sqrt{12} = 2\sqrt{3} \)。
因此,我们已证明\( {PAC} \)是一个等边三角形,其每条边的长度均为\( 2\sqrt{3} \)。
从\( A \)到\( {PC} \)的最短距离是垂线段的长度,记为\( h \),即从\( A \)到\( {PC} \)的垂线长度。因此,\( h \)是等边三角形\( {PAC} \)的高。
我们在第22题的解答中已经看到,边长为\( x \)的等边三角形的高为\( \frac{\sqrt{3}}{2}x \)。由此可得
\[ h = \frac{\sqrt{3}}{2} \times 2\sqrt{3} = 3 \]
供调查
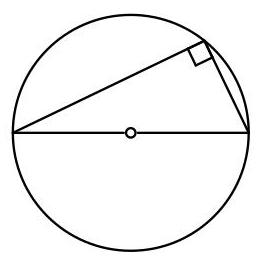
NOTE
上述定理被归于米利都的泰勒斯(Thales of Miletus,约公元前624年—约公元前547年),然而,由于他的著作无一留存,我们无法确定他是否确实证明了这一结果。欲了解更多关于泰勒斯的信息,请访问MacTutor数学史档案:
http://www-history.mcs.st-and.ac.uk
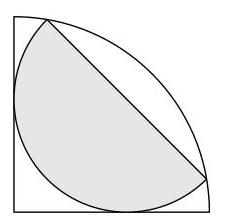
阴影部分占四分之一圆的几分之几?
一种\( \frac{1}{3} \) B \( \frac{1}{\sqrt{3}} \) C \( \frac{2}{3} \) D \( \frac{\sqrt{3}}{2} \) E \( \frac{1}{\sqrt{2}} \)解决方案
设\( O \)为四分之一圆(quarter circle)的圆心,\( A \)和\( B \)为半圆(semicircle)直径的端点,\( M \)为半圆的圆心,因此也是\( {AB} \)的中点。
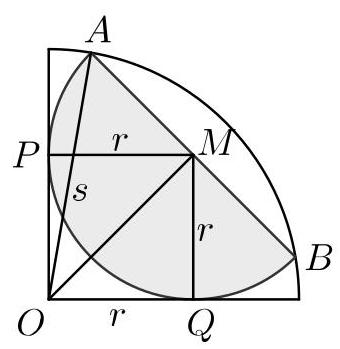
设\( P \)和\( Q \)为四分之一圆与半圆相切处,位于四分之一圆直边上的两点。
我们设四分之一圆的半径为\( s \),半圆的半径为\( r \)。于是\( {OA} = s \)。
由于圆的切线垂直于其半径,\( \angle {OPM} = \angle {OQM} = {90}^{ \circ } \)。又因为\( \angle {POQ} = {90}^{ \circ } \),四边形\( {OQMP} \)的所有角都是直角。同时\( {PM} = r = {QM} \)。因此\( {OPMQ} \)是一个边长为\( r \)的正方形。
将毕达哥拉斯定理(Pythagoras’ theorem)应用于直角三角形\( {OQM} \),得到\( O{M}^{2} = {r}^{2} + {r}^{2} = 2{r}^{2} \)。
三角形\( {AMO} \)在\( M \)处有一个直角。因此,根据毕达哥拉斯定理(Pythagoras’ theorem)应用于该三角形,我们有
\[ A{O}^{2} = O{M}^{2} + M{A}^{2} \]
因此
\[ {s}^{2} = 2{r}^{2} + {r}^{2} \]
\[ = 3{r}^{2}\text{.} \]
四分之一圆的面积为\( \frac{1}{4}\pi {s}^{2} \)。阴影半圆的面积为\( \frac{1}{2}\pi {r}^{2} \)。
因此,四分之一圆中被阴影覆盖的部分所占比例为
\[ \frac{\frac{1}{2}\pi {r}^{2}}{\frac{1}{4}\pi {s}^{2}} = \frac{2{r}^{2}}{{s}^{2}} = \frac{2{r}^{2}}{3{r}^{2}} = \frac{2}{3}. \]