高级数学挑战赛 2018年11月6日(星期二)
由英国数学信托基金会(United Kingdom Mathematics Trust)主办,精算师学院(Faculty Institute of Actuaries)支持

考生须为中学或继续教育学院(FE college)的全日制学生。
英格兰与威尔士:13年级及以下
苏格兰:S6及以下
北爱尔兰:14年级及以下
说明
规定时间结束后,不得再填写答案或个人信息。
3.
可使用空白或横格草稿纸;方格纸、计算器及测量工具禁止使用。
4.
请使用B或HB非活动铅笔。每题在答题卡上最多只能标记A、B、C、D、E中的一个选项,不得多选。
5.
不必期望在限定时间内完成全部试题。本卷题目按难度大致由易到难排列,较难题目位于后部。你无需在时间内完成所有题目,选题时请牢记这一点。
未作答的题目得0分;
每答对一题得4分;
每答错一题扣1分(以抑制猜测)。
7.
你的答题卡将由机器读取。除标记所选选项外,请勿在卡上书写或涂鸦。机器会读取所有黑色铅笔痕迹,即使它们出现在错误位置。若你在错误位置标记,或留下橡皮屑,机器将按自己的方式解读这些痕迹。
8.
本卷题目旨在挑战你的思考,而非鼓励猜测。认真完成一道题比胡乱猜许多答案更能得分,也更有成就感。本卷重在解决有趣的问题,而非靠运气猜答案。
有关高级数学挑战赛(Senior Mathematical Challenge)的咨询请发送至:
英国数学信托(UK Mathematics Trust),利兹大学数学学院,利兹 LS2 9JT
& 01133432339 enquiry@ukmt.org.uk www.ukmt.org.uk 1. 当以下各式求值后,有多少个结果是奇数?\( {1}^{2},{2}^{3},{3}^{4},{4}^{5},{5}^{6} \) A 1 B 2 C 3 D 4 E 5 2. 正整数2018是两个质数的乘积,这两个质数之和是多少?A 1001 B 1010 C 1011 D 1100 E 1101 3. 下列哪一项显示了数字6顺时针旋转\( {135}^{ \circ } \)后的结果?C 9 D E
A \( {2019}^{2} - {2014}^{2} \) B \( {2019}^{2} \times {10}^{2} \) C \( {2020}^{2} \div {101}^{2} \) D \( {2010}^{2} - {2005}^{2} \)
E \( {2015}^{2} \div {5}^{2} \)
A \( \frac{397}{101} \) B \( \frac{487}{121} \) C \( \frac{596}{153} \) D \( \frac{678}{173} \) E \( \frac{796}{203} \)
6.
下列哪一项等于\( {25} \times {15} \times 9 \times {5.4} \times {3.24} \)?A 3 B \( {3}^{10} \) C \( {3}^{11} \) D \( {3}^{14} \) E \( {3}^{17} \)
7.
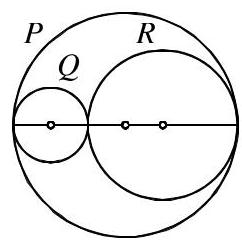
圆\( P, Q \)和\( R \)均彼此外切,它们的圆心都位于\( P \)的一条直径上,如图所示。\( \frac{\text{ circumference of }Q + \text{ circumference of }R}{\text{ circumference of }P} \)的值是多少?A 1 B \( \frac{1}{2} \) C \( \frac{1}{3} \) D \( \frac{1}{4} \) E 需要更多信息 8. \( {7}^{2018} \)的最后两位数字是什么?A 07 B 49 C 43 D 01 E 18
9.
图示为矩形\( {AEFJ} \)位于正十边形\( {ABCDEFGHIJ} \)内部。矩形面积与十边形面积之比是多少?
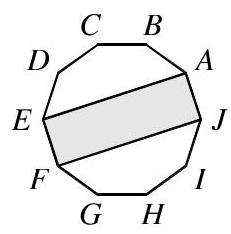
A 2 : 5 B \( 1 : 4 \) C \( 3 : 5 \) D \( 3 : {10} \) E \( 3 : {20} \)
10.
在一次训练骑行中,Laura先以\( {12}\mathrm{\;{km}}/\mathrm{h} \)的速度骑行5分钟,再以\( {15}\mathrm{\;{km}}/\mathrm{h} \)的速度骑行10分钟,最后以\( {18}\mathrm{\;{km}}/\mathrm{h} \)的速度骑行15分钟。
她整个骑行的平均速度是多少?
A \( {13}\mathrm{\;{km}}/\mathrm{h} \) B 14 千米/时 C \( {15}\mathrm{\;{km}}/\mathrm{h} \) D \( {16}\mathrm{\;{km}}/\mathrm{h} \) E \( {17}\mathrm{\;{km}}/\mathrm{h} \)
\( y = {x}^{4} + 1\;y = {x}^{4} + x\;y = {x}^{4} + {x}^{2}\;y = {x}^{4} + {x}^{3} \)
A 0 B 1 C 2 D 3 E 4
12.
正四面体(regular tetrahedron)是一种具有四个面的多面体,每个面都是等边三角形,如图所示。一个实心正四面体被单一平面切割成两块。
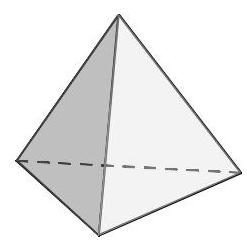
以下哪一项不可能是该切割所得截面的形状?
A 五边形 B 正方形
C 非正方形的矩形 D 梯形
E 非等边三角形
13.
直线 \( y = x \) 与 \( y = {mx} - 4 \) 相交于点 \( P \)。
当 \( P \) 的坐标也是正整数时,所有满足条件的正整数 \( m \) 之和是多少?
A 3 B 5 C 7 D 8 E 10
\( 1, x, x, x, y, y, y, y, y,8,9,{11} \) .
这十二个整数的平均数为 7,则中位数是多少?
A 6 B 7 C 7.5 D 8 E 9
15.
一个正方形内接于半径为 1 的圆。如图所示,一个等腰三角形内接于该正方形。
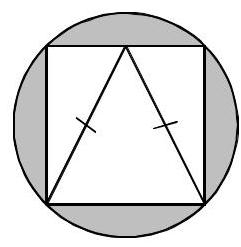
该三角形面积与阴影区域面积之比是多少?
A \( \pi : \sqrt{2} \) B \( \pi : 1 \) C 1 : 4 D \( 1 : \pi - 2 \) E \( 2 : \pi \) 16. 数字\( p, q, r \)和\( s \)满足以下方程:
\[
p + {2q} + {3r} + {4s} = k\;{4p} = {3q} = {2r} = s.
\]
当\( p, q, r \)和\( s \)均为正整数时,\( k \)的最小值是多少?
A 20 B 24 C 25 D 77 E 154
17.
Bethany的钱包里有11枚1英镑硬币、若干枚\( {20}\mathrm{p} \)硬币和若干枚\( {50}\mathrm{p} \)硬币。这些硬币的平均面值为52便士。
以下哪个不可能是钱包中的硬币总数?
A 35 B 40 C 50 D 65 E 95
18.
\( P, Q \)和\( R \)是一个三角形的三个角,每个角均已四舍五入到最接近的度数。
以下哪一项是\( P + Q + R \)所有可能取值的完整列表?
A \( {179}^{ \circ },{180}^{ \circ } \)或\( {181}^{ \circ } \) B \( {180}^{ \circ },{181}^{ \circ } \)或\( {182}^{ \circ } \) C \( {178}^{ \circ },{179}^{ \circ } \)或\( {180}^{ \circ } \) D \( {180}^{ \circ } \)
E \( {178}^{ \circ },{179}^{ \circ },{180}^{ \circ },{181}^{ \circ } \)或\( {182}^{ \circ } \)
“一个正\( m \)边形的外角大小为\( {n}^{ \circ } \),且
一个正\( n \)边形的外角大小为\( {m}^{ \circ } \)。”
A 24 B 22 C 20 D 18 E 16
20.
图示为一个半径为1的半圆位于等腰三角形内部。半圆的直径与三角形的“底边”重合,且三角形中与“底边”相对的角等于\( {2\theta } \)。三角形的两条等边均与半圆相切。
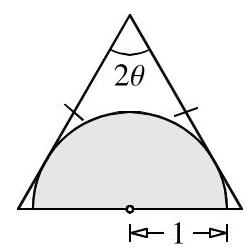
该三角形的面积是多少?
A \( \frac{1}{2}\tan {2\theta } \) B sin \( \theta \cos \theta \) C \( \sin \theta + \cos \theta \) D \( \frac{1}{2}\cos {2\theta } \)
E \( \frac{1}{\sin \theta \cos \theta } \)
21.
\( y = \frac{1}{x} \) 的图像关于直线 \( y = 1 \) 作对称,所得图像再关于直线 \( y = - x \) 作对称。
最终图像的方程是什么?
A \( y = \frac{-1}{\left( x + 2\right) } \) B \( y = \frac{1}{\left( x - 1\right) } \) C \( y = \frac{1}{\left( x - 2\right) } \) D \( y = \frac{-1}{\left( x - 1\right) } \) E \( y = \frac{-1}{\left( x - 2\right) } \)
22.
图示为两个重叠的三角形:一个含 \( {120}^{ \circ } \) 角的等腰三角形,以及一个面积为 36 的等边三角形。等边三角形的两个顶点位于等腰三角形两条等边的中点。
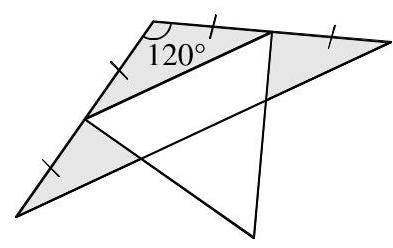
E 32
阴影区域(位于等腰三角形内但在等边三角形外)的总面积是多少?
A 24 B 26 C 28 D 30
23.
对于特定实数 \( a \) 和 \( b \),函数 \( f \) 由 \( f\left( x\right) = {ax} + b \) 定义,且满足 \( f\left( {f\left( {f\left( x\right) }\right) }\right) = {27x} - {52}. \)
以下哪个公式定义了函数 \( g \),使得对所有 \( x, g\left( {f\left( x\right) }\right) = x \) 的值都成立?
A \( \frac{1}{3}x - 4 \) B \( \frac{1}{3}x + \frac{4}{3} \) C \( {4x} - 3 \) D \( \frac{1}{3}x - \frac{4}{3} \) E \( {3x} - 4 \)
24.
图示为一圆,圆心为 \( O \),位于水平面内。直径 \( {AB} \) 长 4。点 \( P \) 在 \( O \) 正上方,且 \( {PO} = 2\sqrt{2} \)。点 \( C \) 位于半圆弧 \( {AB} \) 上,使得弧 \( {AC} \) 与弧 \( {CB} \) 的长度比为 \( 2 : 1 \)。
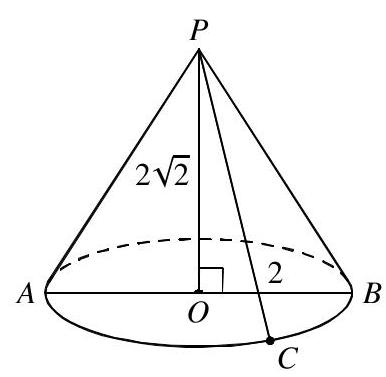
从 \( A \) 到 \( {PC} \) 的最短距离是多少?
A \( \sqrt{2} \) B \( \sqrt{3} \) C 2 D \( 2\sqrt{2} \) E 3
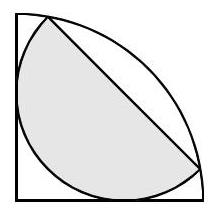
四分之一圆中被阴影覆盖的部分占多少比例?
A \( \frac{1}{3} \) B \( \frac{1}{\sqrt{3}} \) C \( \frac{2}{3} \) D \( \frac{\sqrt{3}}{2} \) E \( \frac{1}{\sqrt{2}} \)









