1.
\( {123}^{2} - {23}^{2} \) 的值是多少?
A 10000 B 10409 C 12323 D 14600 E 15658
2.
\( \left( {{2019} - \left( {{2000} - \left( {{10} - 9}\right) }\right) }\right) - \left( {{2000} - \left( {{10} - \left( {9 - {2019}}\right) }\right) }\right) \) 的值是多少?
A 4040 B 40 C -400 D -4002 E -4020
3.
在测量导线宽度时使用,1 mil(密耳)等于一英寸的千分之一。1 英寸约等于 \( {2.5}\mathrm{\;{cm}} \)。
下列哪一项约等于 1 mil?
A \( \frac{1}{40}\mathrm{\;{mm}} \) B \( \frac{1}{25}\mathrm{\;{mm}} \) C \( \frac{1}{4}\mathrm{\;{mm}} \) D \( {25}\mathrm{\;{mm}} \) E 40 mm
4.
对于多少个正整数 \( n \),\( {n}^{2} + {2n} \) 为素数?
A 0 B 1 C 2 D 3 E 超过 3
5.
Olive Green 想给图中的所有圆着色,使得每个圆恰好有一个同色圆与之相连。
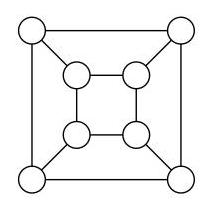
Olive 完成此任务所需的最少颜色数是多少?
A 1 B 2 C 3 D 4 E 5
6.
将 100 的所有因数各放入一个 3×3 网格的单元格中,使得每行、每列及每条对角线上三个数的乘积均相等。图中已给出数字 1、2、50 和 \( x \) 的位置。\( x \) 的值是多少? A 4 B 5 C 10 D 20 E 25
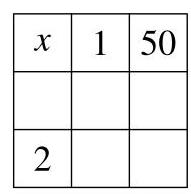
7.
Lucy 被要求从 1、2、3、4 中按某种顺序选取 \( p, q, r \) 和 \( s \),以使 \( \frac{p}{q} + \frac{r}{s} \) 的值尽可能小。
Lucy 用这种方法能得到的最小值是多少?
A \( \frac{7}{12} \) B \( \frac{2}{3} \) C \( \frac{3}{4} \) D \( \frac{5}{6} \) E \( \frac{11}{12} \)
8.
数字\( x \)是方程\( {3}^{\left( {3}^{x}\right) } = {333} \)的解。
以下哪一项是正确的?
A \( 0 < x < 1 \) B \( 1 < x < 2 \) C \( 2 < x < 3 \) D \( 3 < x < 4 \) E \( 4 < x < 5 \)
9.
一张正方形纸对折四次得到更小的正方形,然后如图所示剪掉一个角。
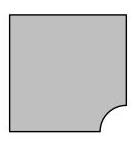
以下哪一项可能是展开后的纸张?
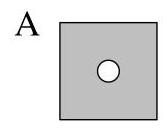
BC D E

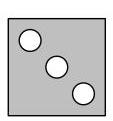
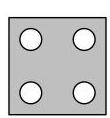
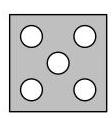
10.
以下五个\( n \)的值中,哪一个是下方框中陈述的反例?
对于正整数\( n \),\( {6n} - 1 \)和\( {6n} + 1 \)中至少有一个是质数。
A 10 B 19 C 20 D 21 E 30
11.
对于多少个整数值的\( k \),\( \sqrt{{200} - \sqrt{k}} \)也是整数?
A 11 B 13 C 15 D 17 E 20
12.
一个半径为1的圆与菱形的各边相切,如图所示。菱形各边之间较小的角为\( {60}^{ \circ } \)。
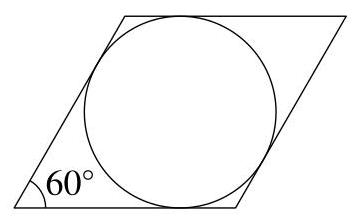
菱形的面积是多少?
A 6 B 4 C \( 2\sqrt{3} \) D \( 3\sqrt{3} \) E \( \frac{8\sqrt{3}}{3} \)
13.
Anish有一些全等的小正方形瓷砖用于马赛克。当他将瓷砖排成边长为\( n \)的正方形时,剩下64块;当他尝试排成边长为\( n + 1 \)的正方形时,缺少25块。
Anish有多少块瓷砖?
A 89 B 1935 C 1980 D 2000 E 2019
14.
下列哪一个是10!的最大平方因子?
注意,\( n! = 1 \times 2 \times 3 \times \cdots \times \left( {n - 1}\right) \times n \)。
A (4!) \( {}^{2} \) B (5!) \( {}^{2} \) C (6!) \( {}^{2} \) D \( {\left( 7!\right) }^{2} \) E \( {\left( 8!\right) }^{2} \)
15.
从正整数\( Q, R \)和\( S \)中任取两数组成的所有数对的最大公因数(highest common factors)是三个不同的质数。
\( Q + R + S \)的最小可能值是多少?
A 41 B 31 C 30 D 21 E 10
16.
数\( x, y \)和\( z \)满足方程\( {9x} + {3y} - {5z} = - 4 \)和\( {5x} + {2y} - {2z} = {13} \)。\( x, y \)和\( z \)的平均值是多少?
A 10 B 11 C 12 D 13 E 14
17.
Jeroen写下2019个连续整数,这些整数的和为2019。
Jeroen列表中所有整数的乘积是多少?
A 20192 B \( \frac{{2019} \times {2020}}{2} \) C 2°2019 D 2019 E 0
18.
Alison将一张正方形纸片沿图中虚线对折。展开后,她再将一个角折到虚线上。
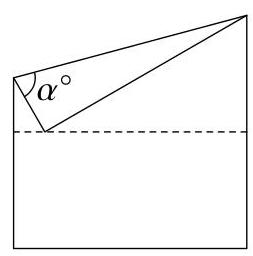
\( \alpha \)的值是多少?
A 45 B 60 C 65 D 70 E 75
19.
下列哪一项可能是\( {y}^{2} = \sin \left( {x}^{2}\right) \)的图像?AB C DE
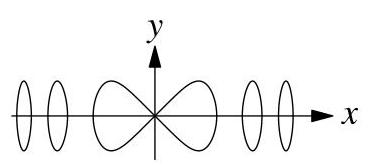
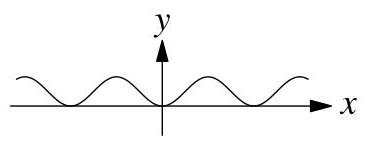
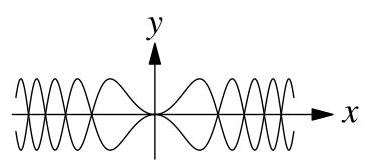
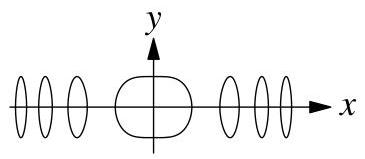
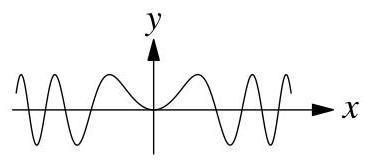
20.
图中所示的“心形”由一个等边三角形\( {ABC} \)和两条全等的半圆组成,半圆位于\( {AB} \)上。两条半圆在点\( P \)相交。点\( O \)是其中一个半圆的圆心。在圆心为\( O \)的半圆上有一点\( X \)。直线\( {XO} \)和\( {XP} \)延长后分别与\( {AC} \)交于\( Y \)和\( Z \)。直线\( {XY} \)和\( {XZ} \)长度相等。
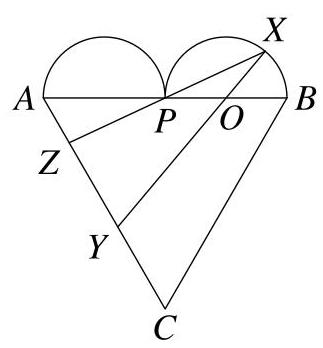
\( \angle {ZXY} \) 是什么?
A 20° B 25° C 30° D 40° E 45°
21.
在边长为 \( {10}\mathrm{\;m} \) 的正方形花园 \( {PQRT} \) 中,一只瓢虫从 \( Q \) 出发,以每分钟 \( {30}\mathrm{\;{cm}} \) 的速度沿边 \( {QR} \) 移动。同时,一只蜘蛛从 \( R \) 出发,以每分钟 \( {40}\mathrm{\;{cm}} \) 的速度沿边 \( {RT} \) 移动。它们之间的最短距离是多少米?
A 5 B 6 C \( 5\sqrt{2} \) D 8 E 10
22.
函数 \( f \) 对所有整数 \( n \) 满足方程 \( \left( {n - {2019}}\right) f\left( n\right) - f\left( {{2019} - n}\right) = {2019} \)。\( f\left( {2019}\right) \) 的值是多少?
A 0 B 1 C \( {2018} \times {2019} \) D \( {2019}^{2} \) E \( {2019} \times {2020} \)
23.
所示实心立方体的棱长为 2。一个平面切割穿过点 \( Y, T, V \) 和 \( W \),这两点均为立方体棱的中点,如图所示。
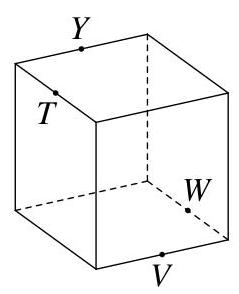
截面的面积是多少?
A \( \sqrt{3} \) B \( 3\sqrt{3} \) C 6 D 6% E 8
24.
数 \( x, y \) 和 \( z \) 由 \( x = \sqrt{{12} - 3\sqrt{7}} - \sqrt{{12} + 3\sqrt{7}}, y = \sqrt{7 - 4\sqrt{3}} - \sqrt{7 + 4\sqrt{3}} \) 和 \( z = \sqrt{2 + \sqrt{3}} - \sqrt{2 - \sqrt{3}}. \) 给出
\( {xyz} \) 的值是多少?
A 1 B -6 C -8 D 18 E 12
25.
两个半径为 1 的圆,每个圆的圆心都位于另一个圆上。一个正方形内接于两圆之间的区域。
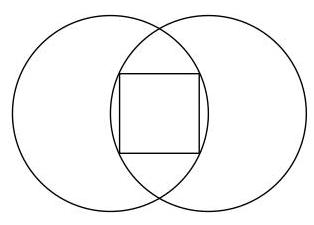
正方形的面积是多少?
A \( 2 - \frac{\sqrt{7}}{2} \) B \( 2 + \frac{\sqrt{7}}{2} \) C \( 4 - \sqrt{5} \) D 1 E \( \frac{\sqrt{5}}{5} \)