SOLUTION
注意:在没有计算器的情况下,解决此题的最佳方法是先进行约分,然后再做除法。此题有多种解法。我们的方法是将分子和分母各除以10两次。
\[ \frac{2020}{{20} \times {20}} = \frac{202}{2 \times {20}} = \frac{20.2}{2 \times 2} = \frac{20.2}{4} = {5.05}. \]
供探究
(a) \( \frac{2020}{2 \times 2} \) ,
(b) \( \frac{2020}{{200} \times {200}} \) ,
(c) \( \frac{2020}{2 \times {200}} \) .
SOLUTION
\( {1234} \times {5678} \) 的个位数字与 \( 4 \times 8 \) 的个位数字相同,因此是2。所以 \( {1234} \times {5678} \) 除以5的余数是2。
供探究
\( {mn} \) 除以11的余数是多少?
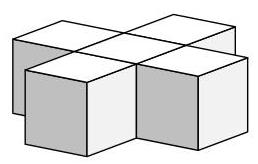
该形状的表面积是多少?
该形状的表面由中心立方体的两个面和其他四个立方体的每个五个面组成。
因此,表面由\( 2 + 4 \times 5 = {22} \)个边长为\( 1 \times 1 \)的正方形面组成。
因此,该形状的表面积为22。
供探究
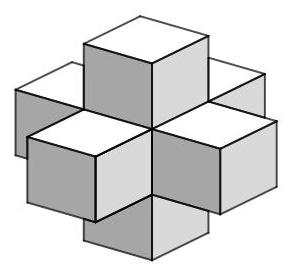
该形状的表面积是多少?
求\( p + q + r + s \)的值?
解决方案
我们有
\[ p = 2, \]
\[ q = \frac{p \times q}{p} = \frac{20}{2} = {10}, \]
\[ r = \frac{p \times q \times r}{p \times q} = \frac{202}{20} = {10.1}, \]
和
\[ s = \frac{p \times q \times r \times s}{p \times q \times r} = \frac{2020}{202} = {10}. \]
因此\( p + q + r + s = 2 + {10} + {10.1} + {10} = {32.1} \)。5. \( \sqrt{123454321} \)是多少? A 1111111 B 111111 C 11111 D 1111 E 111 解决方案
注意:在没有计算器的情况下,你不可能计算出\( \sqrt{123454321} \)的值。因此你需要找到其他方法来选择正确选项。我们使用基于数字123454321大小的方法。
我们有
\[ {10}^{8} < {123454321} < {10}^{10}\text{.} \]
因此
\[ \sqrt{{10}^{8}} < \sqrt{123454321} < \sqrt{{10}^{10}}, \]
也就是说,
\[ {10}^{4} < \sqrt{123454321} < {10}^{5}\text{.} \]
正确的选项因此是唯一介于\( {10}^{4} \)和\( {10}^{5} \)之间的选项。因此,在给定的选项中,等于\( \sqrt{123454321} \)的是11111。
待调查
通过检查\( {11111}^{2} = {123454321} \)来验证\( {11111} = \sqrt{123454321} \)。
有多少学生打曲棍球?
解决方案
因为一半的学生弹钢琴,所以学生人数是2的倍数。
因为四分之一的学生打曲棍球,所以学生人数是4的倍数。
因为七分之一的学生参加学校话剧,所以学生人数是7的倍数。
因此,学生人数是2、4和7的公倍数。故学生人数是28的倍数。
因为班上学生少于30人,所以班上有28名学生。
因此,因为28名学生中有四分之一打曲棍球,打曲棍球的学生人数是7人。
从第一年到第二年,记录在案的茶壶事故大约减少了百分之多少?
SOLUTION
第二年茶壶事故数量的减少是\( {225} - {47} = {178} \)。
178占225的百分比是
\[ \frac{178}{225} \times {100} \approx \frac{180}{225} \times {100} = \frac{20}{25} \times {100} = {20} \times 4 = {80}. \]
SOLUTION
注意:尝试先计算\( {106}^{2} \)和\( {15}^{2} \),再做减法,最后试图分解结果的质因数并不是一个好方法。
我们改用两个平方差的标准因式分解公式:
\[ {x}^{2} - {y}^{2} = \left( {x - y}\right) \left( {x + y}\right) . \]
我们有
\[ {106}^{2} - {15}^{2} = \left( {{106} - {15}}\right) \left( {{106} + {15}}\right) \]
\[ = {91} \times {121} \]
\[ = 7 \times {13} \times {11} \times {11}\text{. } \]
因此,\( {106}^{2} - {15}^{2} \)的质因数分解是\( 7 \times {11}^{2} \times {13} \),由此可见其最大质因数是13。
供研究用
它们相距多少米?
两车之间的距离是以\( {180}\mathrm{\;{km}}/\mathrm{h} \)速度行驶1秒所经过的距离。1公里等于1000米。因此,\( {180}\mathrm{\;{km}} \)中有\( {180} \times {1000} \)米。
每小时有\( {60} \times {60} \)秒。
因此,在\( {180}\mathrm{\;{km}}/\mathrm{h} \)秒内,一辆车行驶了\( {180} \times {1000} \)米。
因此,它在1秒内行驶的米数是
\[ \frac{{180} \times {1000}}{{60} \times {60}} = \frac{3 \times {1000}}{60} = \frac{1000}{20} = {50}. \]
因此,当两车相隔1秒时,它们相距50米。
供研究用
| 速度 | 制动距离 |
| 32 公里/小时 | 12 m |
| 48 公里/小时 | 23 m |
| 64 公里/小时 | 36 m |
| 80 公里/小时 | 53 m |
| 96 公里/小时 | 73 m |
| 112 公里/小时 | 96 m |
对于每个速度,两个以该速度同向行驶的汽车应相隔多少秒,使它们之间的时间距离等于上述表格中对应的停车距离?
《公路规则》给出一辆车以\( {64}\mathrm{\;{km}}/\mathrm{h} \)速度行驶时的反应距离为\( {12}\mathrm{\;m} \)。这对应多少反应时间?
Tara和Uma之间站着多少人?
我们用朋友名字的首字母表示他们,用星号(*)表示尚不确定身份的人。
我们可以不失一般性地假设,从摄影师视角看,Qasim在Pat的右侧。因为Pat和Qasim之间有三个人,队伍排列要么是
\[ * P * * * Q\text{or}P * * * Q * \text{.} \]
Qasim和Roman之间有两个人。Roman不可能在Qasim右侧,因为Qasim右侧最多只有一个朋友。因此Roman在Qasim左侧,队伍排列要么是
\[ * {PR} * * Q\text{or}{PR} * * Q * \text{.} \]
Roman和Sam之间有一个人。因此Sam要么紧挨Pat左侧,要么紧挨Qasim左侧。
如果Sam紧挨Pat左侧,队伍排列将是
\[ {SPR} * * Q\text{.} \]
但这不可能,因为Sam不在队伍任一端。
因此Sam紧挨Qasim左侧。故队伍排列要么是
\[ * {PR} * {SQ}\text{or}{PR} * {SQ} * \]
Tara和Uma占据两个星号标记的位置。
无论Tara和Uma如何占据这两个位置,Tara和Uma之间站着的人数都是2。
待探究
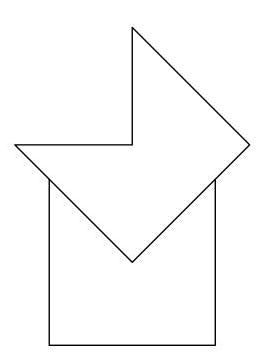
所形成的八边形的周长长度是多少?
设 \( P, Q, R, S, T, U, V \) 和 \( W \) 是八边形的顶点,如图所示,\( X \) 是图中所示的顶点。
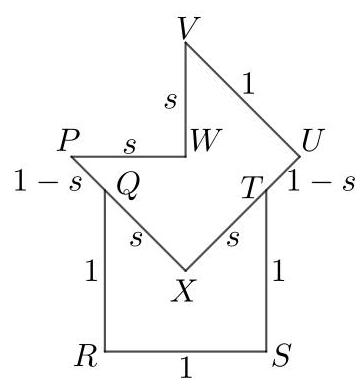
边 \( {PX},{XU},{UV},{QR},{RS} \) 和 \( {ST} \) 的长度均为1。
设 \( {PW} \) 的长度为 \( s \)。由于 \( {PWV} \) 是一个直角等腰三角形,\( {VW} \) 的长度也为 \( s \)。
因为五边形 \( {PXUVW} \) 和 \( {QRSTX} \) 全等,\( {QX} \) 和 \( {TX} \) 的长度也均为 \( s \)。
由此可得 \( {PQ} \) 和 \( {TU} \) 的长度均为 \( 1 - s \)。
我们现在可以推导出八边形 \( {PQRSTUVW} \) 的周长长度为
\[ \left( {1 - s}\right) + 1 + 1 + 1 + \left( {1 - s}\right) + 1 + s + s = 6. \]
评注
注意,为了计算周长长度,我们不需要知道 \( s \) 的具体数值。然而,求出 \( s \) 的值并不困难。你将在问题11.1中被要求完成此项。
供探究
解答
我们设一件夹克、一条裤子和一件马甲的价格分别为\( \pounds J,\pounds T \)和\( \pounds W \)。
根据题中给出的信息,我们可以推导出
\[ {2J} + {3T} = {380} \tag{1} \]
和
\[ T = {2W} \tag{2} \]
注意:本题中我们有三个未知数\( J, T \)和\( W \),但只有两个方程。信息不足以求出\( J, T \)和\( W \)的具体数值。然而,我们可以推导出\( J + T + W \)的值,这正是我们需要知道的。以下给出两种方法。
方法一
如果用方程(1)减去方程(2),我们得到
\[ {2J} + {2T} = {380} - {2W}. \]
因此
\[ {2J} + {2T} + {2W} = {380}. \]
因此,将上述方程两边同时除以2,我们得到
\[ J + T + W = {190} \]
所以,一套三件套西服的价格是\( \pounds {190} \)。
方法二
由方程(2)可得\( W = \frac{1}{2}T \)。因此,
\[ J + T + W = J + T + \frac{1}{2}T \]
\[ = J + \frac{3}{2}T \]
\[ = \frac{1}{2}\left( {{2J} + {3T}}\right) \]
\[ = \frac{1}{2}\left( {380}\right) ,\;\text{ by equation }\left( 1\right) , \]
\[ = {190}\text{.} \]
所以,一套三件套西服的价格是\( \pounds {190} \)。
SOLUTION
我们要找的数字\( k \)满足\( {16}! = {2}^{k} \times q \),其中\( q \)是一个奇整数。因此,\( k \)是16!的质因数分解中2的幂次。
方法一
要找出16!中包含的最大2的幂次,只需考虑乘积中出现的偶数\( 1 \times 2 \times \cdots \times {15} \times {16} \),这些偶数构成了16!的值。
下表列出了能够整除这些因数的2的幂次。
| 因子 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | |
| 2的幂 | 1 | 2 | 1 | 3 | 1 | 2 | 1 | 4 |
16的质因数分解中2的幂次:是本表第二行幂次的总和。也就是说,它是\( 1 + 2 + 1 + 3 + 1 + 2 + 1 + 4 = {15} \) 。
因此,所求的\( k \)值是15 。
方法二
注意:
在此方法中,我们使用通常归功于法国数学家阿德里安-玛丽·勒让德(Adrian-Marie Legendre,1752-1833)的公式,求解质数\( p \)在\( n \)!中出现的最高幂次。该公式使用了下取整函数,下面先进行解释。
我们定义\( x \)的下取整,记作\( \lfloor x\rfloor \),为不大于\( x \)的最大整数。
例如,\( \lfloor 2\frac{6}{7}\rfloor = 2,\lfloor {4.275}\rfloor = 4,\lfloor \pi \rfloor = 3,\lfloor 7\rfloor = 7,\lfloor {0.43}\rfloor = 0 \)和\( \lfloor - {5.23}\rfloor = - 6 \)。
根据勒让德公式,质数\( p \)在\( n \)!中出现的最高幂次由下式给出
\[ \left\lfloor \frac{n}{p}\right\rfloor + \left\lfloor \frac{n}{{p}^{2}}\right\rfloor + \left\lfloor \frac{n}{{p}^{3}}\right\rfloor + \ldots \]
乍一看,该公式涉及无限求和。然而,若\( {p}^{k} > n \),则有\( 0 < \frac{n}{{p}^{k}} < 1 \),从而\( \left\lfloor \frac{n}{{p}^{k}}\right\rfloor = 0 \)。因此,上述求和中只有有限项非零。非零项的数量是满足\( {p}^{k} \leq n \)的最大整数\( k \)。
根据勒让德公式,2在16!中出现的最高幂次是\( k \),其中
\[ k = \left\lfloor \frac{16}{2}\right\rfloor + \left\lfloor \frac{16}{{2}^{2}}\right\rfloor + \left\lfloor \frac{16}{{2}^{3}}\right\rfloor + \left\lfloor \frac{16}{{2}^{4}}\right\rfloor \]
\[ = \left\lfloor \frac{16}{2}\right\rfloor + \left\lfloor \frac{16}{4}\right\rfloor + \left\lfloor \frac{16}{8}\right\rfloor + \left\lfloor \frac{16}{16}\right\rfloor \]
\[ = \left\lfloor 8\right\rfloor + \left\lfloor 4\right\rfloor + \left\lfloor 2\right\rfloor + \left\lfloor 1\right\rfloor \]
\[ = 8 + 4 + 2 + 1 \]
\[ = {15}\text{.} \]
供探究
也就是说,证明质数 \( p \) 在 \( n \) ! 中的最高幂次由下述和式给出
\[ \left\lfloor \frac{n}{p}\right\rfloor + \left\lfloor \frac{n}{{p}^{2}}\right\rfloor + \left\lfloor \frac{n}{{p}^{3}}\right\rfloor + \cdots + \left\lfloor \frac{n}{{p}^{k}}\right\rfloor , \]
其中 \( k \) 是满足 \( {p}^{k} \leq n \) 的最大整数。
她能摆出多少种不同的完整网格?
注意:此类问题的关键是决定考虑不同颜色圆盘放置顺序的策略。在本题中,最好先考虑两个红色圆盘的不同放置方式,因为它们必须满足不放在相邻格子的条件。
在图中,我们给格子编号以便引用。
如果第一个红色圆盘放在格子 \( P \) ,那么第二个红色圆盘可以放在任意一个格子 \( R, S, U, V \) 和 \( W \) 中的5个格子里。
同样,如果它放在任一格子 \( S, T \) 和 \( Q \) 中,第二个红色圆盘有5个可能的格子可选。
如果第一个红色圆盘放在任一格子 \( Q, R, U \) 和 \( V \) 中,第二个红色圆盘有4个选择。
这样共有 \( 5 \times 4 + 4 \times 4 = {36} \) 种放置两个红色圆盘的方法,但每对格子组合被计算了两次。
因此,放置两个红色圆盘的不同方式共有 \( {36} \div 2 = {18} \) 种。
红色圆盘放好后,黄色圆盘可以放在剩下的6个格子中的任意一个。
一旦红色和黄色圆盘放置完毕,5个蓝色圆盘必须放在剩余的5个空格中。这样只有一种放法。
这就产生了\( {18} \times 6 \times 1 = {108} \)种不同外观的填充方式。
供研究用
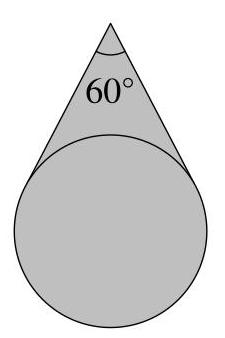
阴影面积是多少?
解答
设\( O \)为圆心,\( {PS} \)和\( {PT} \)为圆的切线,如图所示。
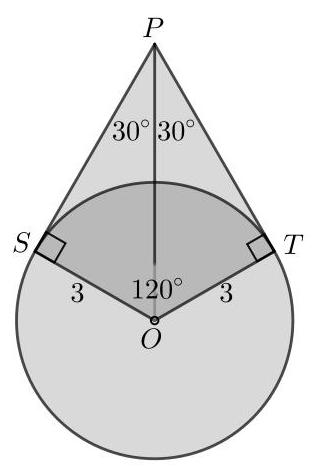
在三角形\( {PSO} \)和\( {PTO} \)中,由于\( {PS} \)和\( {PT} \)是圆的切线,故有\( \angle {PSO} = \angle {PTO} = {90}^{ \circ } \);\( {SO} = {TO} \),因为它们是同一圆的半径;且边\( {PO} \)是公共边。
因此,这两个三角形全等(RHS)。故\( \angle {SPO} = \angle {TPO} = {30}^{ \circ } \)。
由此可得\( \frac{OS}{PS} = \tan {30}^{ \circ } = \frac{1}{\sqrt{3}} \)。
因此\( {PS} = {OS}\sqrt{3} = 3\sqrt{3} \)。
利用三角形面积公式 \( = \frac{1}{2} \)(底边 \( \times \) 高度),可得三角形 \( {PSO} \) 的面积为 \( \frac{1}{2}\left( {{OS} \times {PS}}\right) = \frac{1}{2}\left( {3 \times 3\sqrt{3}}\right) = \frac{1}{2}\left( {9\sqrt{3}}\right) \) 。
这也是全等三角形 PTO 的面积。因此这两个三角形面积之和为 \( 9\sqrt{3} \) 。
总阴影面积是这两个三角形面积之和加上圆中位于这两个三角形外部的部分面积。因为 \( \angle {SOT} = {120}^{ \circ } \) ,圆中位于这两个三角形外部的部分占圆的三分之二,因此其面积为
\[ \frac{2}{3}\left( {\pi \times {3}^{2}}\right) = {6\pi } \]
因此阴影面积为 \( {6\pi } + 9\sqrt{3} \) 。
待探究
解释为什么这是正确的。
BD
\( x \) - \( x \) E
解答 E
我们有
\[ {y}^{2} - {2y} = {x}^{2} + {2x} \Leftrightarrow {y}^{2} - {x}^{2} - {2y} - {2x} = 0 \]
\[ \Leftrightarrow \left( {y - x}\right) \left( {y + x}\right) - 2\left( {y + x}\right) = 0 \]
\[ \Leftrightarrow \left( {y - x - 2}\right) \left( {y + x}\right) = 0 \]
\[ \Leftrightarrow y - x - 2 = 0\;\text{ or }\;y + x = 0 \]
\[ \Leftrightarrow y = x + 2\;\text{ or }\;y = - x. \]
注:另一种方法是对方程两边完成平方。见下文问题 16.1。
因此我们看到,满足方程 \( {y}^{2} - {2y} = {x}^{2} + {2x} \) 的点集由满足方程 \( y = x + 2 \) 的直线上的所有点和满足方程 \( y = - x \) 的直线上的所有点组成。

方程为 \( y = x + 2 \) 的直线是斜率为1且经过点 (0,2) 的直线。
方程为\( y = - x \)的直线是斜率为-1且经过点(0,0)的直线。显示这两条直线的图形是选项\( \mathrm{E} \)中的图。
待探究
因为\( \frac{3}{n + \frac{1}{p}} = {17} - {3m} \),且\( m \)是整数,所以\( \frac{3}{n + \frac{1}{p}} \)也是整数。
因为\( n \)和\( p \)是正整数,故\( 1 < n + \frac{1}{p} \),因此\( 0 < \frac{3}{n + \frac{1}{p}} < 3 \)。所以\( \frac{3}{n + \frac{1}{p}} \)只能是1或2。如果\( \frac{3}{n + \frac{1}{p}} = 1 \),则\( {3m} = {17} - \frac{3}{n + \frac{1}{p}} = {17} - 1 = {16} \)。这意味着\( m = \frac{16}{3} \),与\( m \)是整数的事实矛盾。因此\( \frac{3}{n + \frac{1}{p}} = 2 \)。所以\( n + \frac{1}{p} = \frac{3}{2} = 1 + \frac{1}{2} \)。因此\( n = 1 \)和\( p = 2 \)。同时\( {3m} = {17} - \frac{3}{1 + \frac{1}{2}} = {17} - 2 = {15} \),所以\( m = 5 \)。由此我们看到\( m = 5, n = 1 \)和\( p = 2 \)。
两个圆\( {C}_{1} \)和\( {C}_{2} \)的半径之和是多少?
设\( P \)为圆\( {C}_{1} \)的圆心,\( {C}_{2}, O \)为圆\( {C}_{3} \)的圆心,\( R \)和\( S \)分别为圆\( {C}_{1} \)和\( {C}_{2} \)与\( {C}_{3} \)的切点。设圆\( {C}_{1} \)的半径为\( r \)。
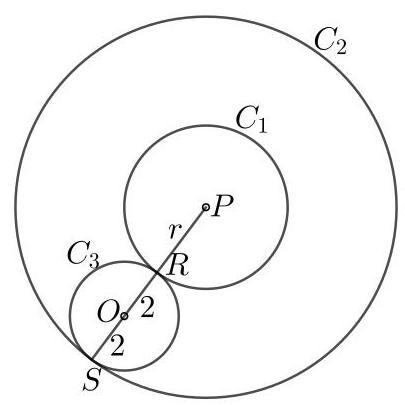
注意点\( O, P, R \)和\( S \)共线。
根据勾股定理,坐标为(3,4)的点\( P \)与坐标为(0,0)的点\( O \)之间的距离是\( \sqrt{{3}^{2} + {4}^{2}} = \sqrt{25} = 5 \)。
因此,\( r + 2 = 5 \),从而\( r = 3 \)。
圆\( {C}_{2} \)的半径是\( r + 2 + 2 = 3 + 2 + 2 = 7 \)。
因此,\( {C}_{1} \)和\( {C}_{2} \)的半径之和是\( 3 + 7 = {10} \)。
待研究
因为\( r = p - q \),所以有\( t = r - s = \left( {p - q}\right) - s = p - \left( {q + s}\right) \)。
由此可知,当\( p \)取最大值且\( q + s \)取最小值时,\( t \)的最大值出现。
\( p \)的最大值是9。
因为\( q \)和\( s \)取不同值,\( q + s \)的最小值是\( 1 + 2 = 3 \)。
因此,\( t \)的最大可能值是\( 9 - 3 = 6 \)。
下表显示\( t \)可以取从1到6的所有正整数值。
| \( p \) | \( q \) | \( r \) | \( S \) | \( t \) | |
| 9 | 1 | 8 | 2 | 6 | |
| 9 | 1 | 8 | 3 | 5 | |
| 9 | 2 | 7 | 3 | 4 | |
| 9 | 2 | 7 | 4 | 3 | |
| 9 | 3 | 6 | 4 | 2 | |
| 9 | 3 | 6 | 5 | 1 |
因此,\( t \) 可以取的值有6个。
待调查
解决方案
我们有 \( {4}^{y} = {\left( {2}^{2}\right) }^{y} = {2}^{2y} \),和 \( \frac{1}{8{\left( \sqrt{2}\right) }^{x + 2}} = \frac{1}{{2}^{3}{\left( {2}^{\frac{1}{2}}\right) }^{x + 2}} = {2}^{-\left( {3 + \frac{1}{2}\left( {x + 2}\right) }\right) } \)。
因此,从方程 \( {4}^{y} = \frac{1}{8{\left( \sqrt{2}\right) }^{x + 2}} \) 中我们推导出 \( {2y} = - \left( {3 + \frac{1}{2}\left( {x + 2}\right) }\right) \)。
因此
\[ y = - \frac{1}{4}x - 2 \tag{1} \]
此外,\( {9}^{x} \times {3}^{y} = {\left( {3}^{2}\right) }^{x} \times {3}^{y} = {3}^{{2x} + y} \) 和 \( 3\sqrt{3} = \left( {3}^{1}\right) \left( {3}^{\frac{1}{2}}\right) = {3}^{1 + \frac{1}{2}} = {3}^{\frac{3}{2}} \)。
因此,从方程 \( {9}^{x} \times {3}^{y} = 3\sqrt{3} \) 中我们推导出 \( {2x} + y = \frac{3}{2} \)。
因此
\[ y = - {2x} + \frac{3}{2}. \tag{2} \]
由方程(1)和(2)
\[ - \frac{1}{4}x - 2 = - {2x} + \frac{3}{2}. \]
最后这个方程可以重新排列为
\[ \frac{7}{4}x = \frac{7}{2} \]
因此 \( x = 2 \)。
因此,由方程 \( \left( 1\right) , y = - \frac{5}{2} \) 得出。
由此可得 \( x + y = 2 + \left( {-\frac{5}{2}}\right) = 2 - \frac{5}{2} = - \frac{1}{2} \) 。
因此 \( {5}^{x + y} = {5}^{-\frac{1}{2}} = \frac{1}{\sqrt{5}} \) 。待研究
\[ {\left( \sqrt{3}\right) }^{x} \times {3}^{y} = \sqrt[5]{27} \]
和
\[ {8}^{x} \times {\left( \sqrt{2}\right) }^{y} = \sqrt[3]{4} \]
求 \( {8}^{x + y} \) 的值。21. 当完整写出数字 \( {\left( {10}^{2020} + {2020}\right) }^{2} \) 时,它有4041位。这个4041位数字的各位数字之和是多少?A 9 B 17 C 25 D 2048 E 4041
SOLUTION
利用展开式 \( {\left( x + y\right) }^{2} = {x}^{2} + {2xy} + {y}^{2} \) ,我们有
\[ {\left( {10}^{2020} + {2020}\right) }^{2} = {\left( {10}^{2020}\right) }^{2} + 2 \times {10}^{2020} \times {2020} + {2020}^{2} \]
\[ = {10}^{4040} + {4040} \times {10}^{2020} + {4080400}. \tag{1} \]
我们注意到,当我们将三个项 \( {10}^{4040},{4040} \times {10}^{2002} \) 和 408040 相加时,没有两个非零数字出现在同一列:
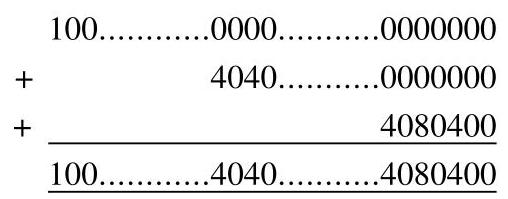
因此,最终答案中的非零数字正好是上述(1)中三个项的非零数字。
因此数字 \( {\left( {10}^{2020} + {2020}\right) }^{2} \) 中各位数字之和为
\[ 1 + 4 + 4 + 4 + 8 + 4 = {25} \]
评注
最终答案中0的确切数量并不重要。重要的是三个项 \( {10}^{4040},{4040} \times {10}^{2020} \) 和 4080400 中的非零数字位于不同的列,因此相加时,最终答案中的非零数字正是这些项中的非零数字。然而,下面的21.1题要求你计算0的数量。
待研究

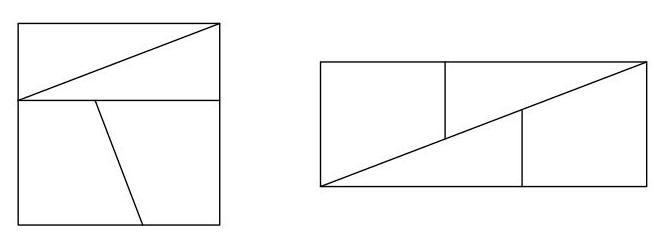
这个矩形的周长是多少厘米?
SOLUTION
该正方形的周长为 \( 4\mathrm{\;{cm}} \),因此其边长均为 \( 1\mathrm{\;{cm}} \) 。
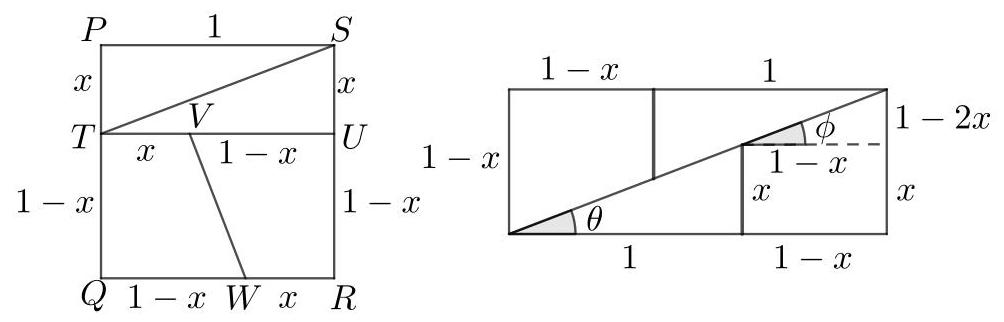
令左侧图中的顶点按图示标记。
我们设 \( {SU} \) 的长度为 \( x\mathrm{\;{cm}} \) 。
为了使各部分如右图所示拼合,\( {TV} \) 和 \( {WR} \) 也必须具有长度 \( x\mathrm{\;{cm}} \) 。由此可知,其他长度,在 \( \mathrm{{cm}} \) 中,如图所示。
方法一
为了使各部分拼合,角 \( \phi \) 和 \( \theta \) 必须相等,如上图右侧所示。因此 \( \tan \phi = \tan \theta \) 。即,
\[ \frac{1 - {2x}}{1 - x} = \frac{x}{1} \]
因此
\[ 1 - {2x} = x\left( {1 - x}\right) \text{.} \]
最后这个方程可以重新排列为
\[ {x}^{2} - {3x} + 1 = 0 \]
根据二次方程解的标准公式 \( \frac{-b \pm \sqrt{{b}^{2} - {4ac}}}{2a} \),我们可以
推导出
\[ x = \frac{3 \pm \sqrt{5}}{2} \]
由于 \( x < 1 \),故 \( x = \frac{3 - \sqrt{5}}{2} \) 。
从上方右侧的图中可见,矩形的周长为
\[ \left( {1 - x}\right) + \left( {2 - x}\right) + \left( {1 - x}\right) + \left( {2 - x}\right) = 6 - {4x} = 6 - 4\left( \frac{3 + \sqrt{5}}{2}\right) = 2\sqrt{5}. \]
方法二
由于它们由相同的两个三角形和两个梯形组成,矩形的面积等于正方形的面积。
因此,根据上图,我们有
\[ \left( {1 + \left( {1 - x}\right) }\right) \times \left( {1 - x}\right) = 1 \times 1 \]
也就是说,
\[ \left( {2 - x}\right) \left( {1 - x}\right) = 1\text{.} \]
因此
\[ 2 - {3x} + {x}^{2} = 1 \]
所以
\[ {x}^{2} - {3x} + 1 = 0 \]
因此,如方法\( 1, x = \frac{3 - \sqrt{5}}{2} \)中所示,矩形的周长是\( 2\sqrt{5} \)。
待探究
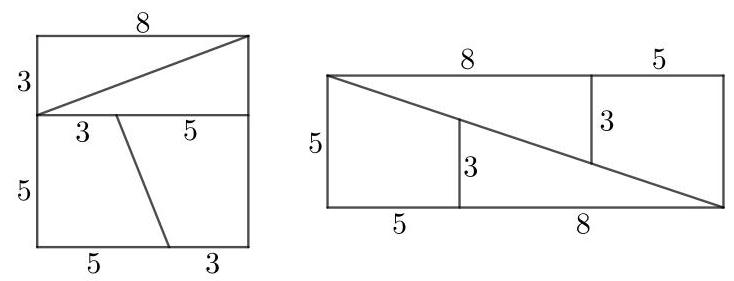
上图左侧显示一个\( 8 \times 8 \)正方形被分成四块,这些块重新排列后形成右侧所示的\( {13} \times 5 \)矩形。
然而\( 8 \times 8 < {13} \times 5 \)。
额外的面积从何而来?
注:此谜题归功于威廉·胡珀(William Hooper),见其1774年著作《理性娱乐》(Rational Recreations)。
将\( x = {20} \)和\( y = 3 \)代入方程\( {y}^{3}f\left( x\right) = {x}^{3}f\left( y\right) \),得到\( {27f}\left( {20}\right) = {8000f}\left( 3\right) \)。
因此
\[ f\left( {20}\right) = \frac{8000}{27}f\left( 3\right) . \]
将\( x = 2 \)和\( y = 3 \)代入同一方程,得到\( {27f}\left( 2\right) = {8f}\left( 3\right) \)。因此
\[ f\left( 2\right) = \frac{8}{27}f\left( 3\right) . \]
所以,
\[ f\left( {20}\right) - f\left( 2\right) = \frac{8000}{27}f\left( 3\right) - \frac{8}{27}f\left( 3\right) \]
\[ = \left( {\frac{8000}{27} - \frac{8}{27}}\right) f\left( 3\right) \]
\[ = \frac{7992}{27}f\left( 3\right) \]
\[ = {296f}\left( 3\right) \text{.} \]
因此,因为\( f\left( 3\right) \neq 0 \),可得
\[ \frac{f\left( {20}\right) - f\left( 2\right) }{f\left( 3\right) } = {296} \]
待探究
\[ \frac{f\left( {46}\right) - f\left( {23}\right) }{f\left( {23}\right) } \]
\[ \frac{f\left( x\right) - f\left( y\right) }{f\left( z\right) } = 7. \]
\[ \frac{f\left( x\right) - f\left( y\right) }{f\left( z\right) } = n \]
要么有无限多个正整数 \( x, y \) 和 \( z \) 的解,要么无此类解。
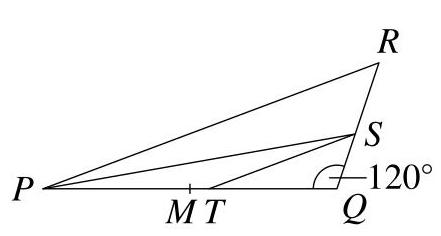
\( {SQ} \) 的长度是多少?
解答
设 \( t \) 为 \( {SQ} \) 的长度。
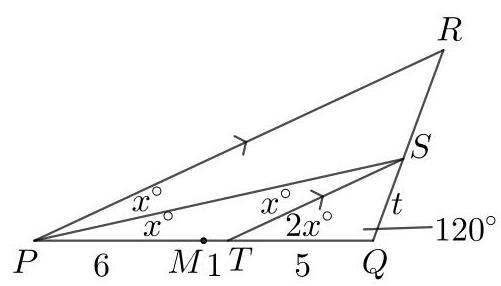
设 \( \angle {QPS} = {x}^{ \circ } \) 。
因为 \( {PQ} \) 长度为12,且 \( M \) 是 \( {PQ} \) 的中点,故 \( {MP} \) 长度为6。已知 \( {MT} \) 长度为1。因此 \( {PT} \) 长度为7,\( {TQ} \) 长度为5。
因为 \( {PS} \) 平分 \( \angle {RPQ} \),所以 \( \angle {RPS} = \) \( \angle {QPS} = {x}^{ \circ } \) 。因此 \( \angle {RPQ} = 2{x}^{ \circ } \) 。
因为 \( {ST} \) 平行于 \( {PR} \),所以 \( \angle {STQ} = \angle {RPQ} = 2{x}^{ \circ } \) 。
根据外角定理(参见问题24.1),应用于三角形PTS,得出 \( \angle {PST} = {x}^{ \circ } \) 。
因此三角形 \( {PST} \) 是等腰三角形,故 \( {ST} \) 与 \( {PT} \) 长度相同,均为7。现对三角形 \( {STQ} \) 应用余弦定理,得到
\[ {7}^{2} = {5}^{2} + {t}^{2} - 2\left( {{5t}\cos {120}^{ \circ }}\right) . \]
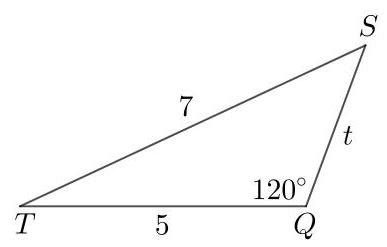
因此,作为\( \cos {120}^{ \circ } = - \frac{1}{2} \),
\[ {49} = {25} + {t}^{2} + {5t} \]
因此\( {t}^{2} + {5t} - {24} = 0 \)。因此\( \left( {t - 3}\right) \left( {t + 8}\right) = 0 \)。所以\( t \)要么是3,要么是-8。由于\( t \)对应长度,\( t > 0 \)。我们推断出\( t = 3 \)。
待调查
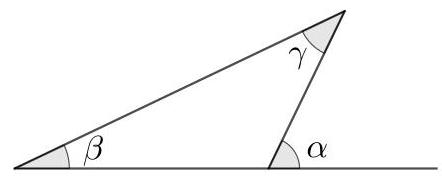
就图示而言,它表示\( \alpha = \beta + \gamma \)。
解释为什么外角定理成立。
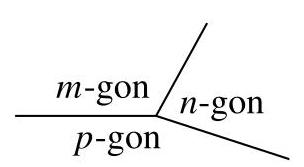
\( p \)的最大可能值是多少?
一个有\( m \)条边的多边形的内角和是\( \left( {m - 2}\right) {180}^{ \circ } \)【参见问题25.1】。因此,正\( m \)边形的每个内角是\( \left( \frac{m - 2}{m}\right) {180}^{ \circ } \),正\( n \)边形和正\( p \)边形亦然。由于一点处角度和为\( {360}^{ \circ } \),我们有
\[ \left( \frac{m - 2}{m}\right) {180} + \left( \frac{n - 2}{n}\right) {180} + \left( \frac{p - 2}{p}\right) {180} = {360}. \]
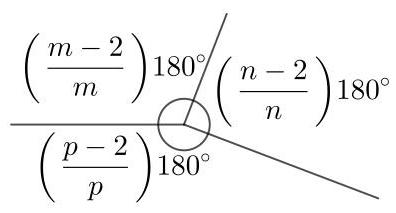
由此得出
\[ \frac{m - 2}{m} + \frac{n - 2}{n} + \frac{p - 2}{p} = 2 \]
我们可以将最后这个方程重写为\( \left( {1 - \frac{2}{m}}\right) + \left( {1 - \frac{2}{n}}\right) + \left( {1 - \frac{2}{p}}\right) = 2 \)。因此
\[ \frac{1}{m} + \frac{1}{n} + \frac{1}{p} = \frac{1}{2} \tag{1} \]
注意到由于\( p \)是正整数,由(1)式可知\( \frac{1}{m} + \frac{1}{n} < \frac{1}{2} \)。(2)
我们寻求(1)式的解,其中\( m, n \)和\( p \)为正整数,且\( p \)尽可能大。为了使\( p \)最大,\( \frac{1}{p} \)需尽可能小。因此,根据(1)式,\( \frac{1}{m} + \frac{1}{n} \)需尽可能大,且满足不等式(2)。故\( m \)和\( n \)需尽可能小。且不失一般性,我们可假设\( m \leq n \)。
根据(2)式,\( m \geq 3 \)。若\( m = 3 \),则\( \frac{1}{n} < \frac{1}{2} - \frac{1}{3} = \frac{1}{6} \),因此\( n > 6 \)。当\( m = 3 \)且\( n = 7 \)时,我们有\( \frac{1}{m} + \frac{1}{n} = \frac{1}{3} + \frac{1}{7} = \frac{10}{21} \)。因此,根据(1)式,\( \frac{1}{p} = \frac{1}{2} - \frac{10}{21} = \frac{1}{42} \),故\( p = {42} \)。我们证明这给出了\( p \)的最大可能值。
我们不能有\( m = n = 4 \),因为这与不等式(2)不兼容。
如果\( n > m \geq 4 \),则有\( \frac{1}{m} + \frac{1}{n} \leq \frac{1}{4} + \frac{1}{5} = \frac{9}{20} < \frac{10}{21} \),因此\( \frac{1}{m} + \frac{1}{n} \)不会达到最大值。
因此,\( p \)的最大可能值由\( m = 3, n = 7 \)和\( p = {42} \)给出。