1.
\( \frac{2020}{{20} \times {20}} \) 的值是多少?
A 10.1 B 5.5 C 5.1 D 5.05 E 0.55
2.
\( {1234} \times {5678} \) 除以 5 的余数是多少?
A 0 B 1 C 2 D 3 E 4
3.
如图所示,一个形状由五个单位立方体组成。
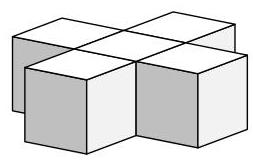
该形状的表面积是多少?
A 22 B 24 C 26 D 28 E 30
4.
数 \( p, q, r \) 和 \( s \) 满足方程 \( p = 2, p \times q = {20}, p \times q \times r = {202} \) 和 \( p \times q \times r \times s = {2020}. \)
\( p + q + r + s \) 的值是多少?
A 32 B 32.1 C 33 D 33.1 E 34
5.
\( \sqrt{123454321} \) 等于多少?
A 1111111 B 111111 C 11111 D 1111 E 111
6.
A-level 数学班的学生不足 30 人。其中一半会弹钢琴,四分之一打曲棍球,七分之一参加学校戏剧演出。
有多少名学生打曲棍球?
A 3 B 4 C 5 D 6 E 7
7.
英国官方事故统计显示,某年共发生 225 起涉及茶壶的事故。然而,次年此类事故仅有 47 起。
从第一年到第二年,涉及茶壶的已记录事故大约减少了百分之多少?
A 50% B 60% C 70% D 80% E 90%
8.
\( {106}^{2} - {15}^{2} \) 的最大质因数是多少?
A 3 B 7 C 11 D 13 E 17
9.
2018年,赛车手被允许在赛车与前车相距1秒以内时使用减阻系统(Drag Reduction System)。假设两车相距1秒,均以180 \( \mathrm{{km}}/\mathrm{h} \) 同向行驶。
它们相距多少米?
A 100 B 50 C 10 D 5 E 1
10.
六位朋友Pat、Qasim、Roman、Sam、Tara和Uma排成一行拍照。Pat和Qasim之间站了三人,Qasim和Roman之间站了两人,Roman和Sam之间站了一人。Sam不在队伍两端。
Tara和Uma之间站了多少人?
A 4 B 3 C 2 D 1 E 0
11.
两个全等的五边形各由边长为1的正方形去掉一个等腰直角三角形而成。随后将这两个五边形按图示拼合。
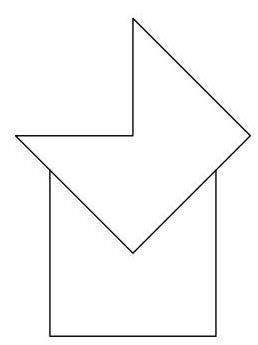
所形成八边形的周长是多少?
A 4 B \( 4 + 2\sqrt{2} \) C 5 D \( 6 - 2\sqrt{2} \)
12.
一套三件套西装包括一件夹克、一条裤子和一件马甲。两件夹克和三条裤子共\( \pounds {380} \)。一条裤子的价格等于两件马甲。
一套三件套西装的价格是多少?
A £150 B £190 C £200 D £228
需要更多信息
13.
数\( {16}! \div {2}^{k} \)是一个奇整数。注意\( n! = 1 \times 2 \times 3 \times \cdots \times \left( {n - 1}\right) \times n \)。
\( k \)的值是多少?
A 9 B 11 C 13 D 15 E 17
14.
Diane有五张相同的蓝色圆盘、两张相同的红色圆盘和一张黄色圆盘。她想把它们放在对面的网格中,使每个格子恰好包含一张圆盘。两张红色圆盘不能放在共享一条公共边的格子里。
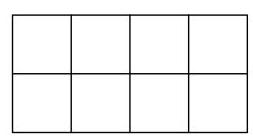
她能制作出多少种不同外观的完成网格?
A 96 B 108 C 144 D 180 E 216
15.
图中所示的阴影区域由一个半径为3的圆的内部以及圆与两条切线之间的区域组成。两条切线在它们相交点处的夹角为\( {60}^{ \circ } \)。
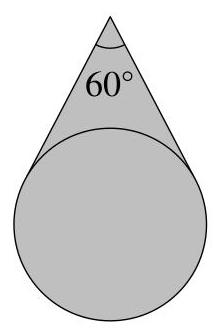
阴影区域的面积是多少?
A \( {6\pi } + 9\sqrt{3} \) B \( {15}\sqrt{3} \) C \( {9\pi } \) D \( {9\pi } + 4\sqrt{3} \) E \( {6\pi } + \frac{9\sqrt{3}}{4} \)
16.
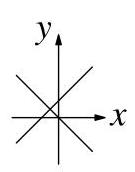
哪个图表示满足\( {y}^{2} - {2y} = {x}^{2} + {2x} \)的所有点(x, y)的集合?
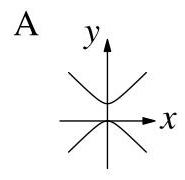
BC D E
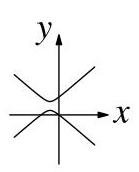
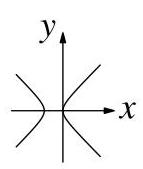
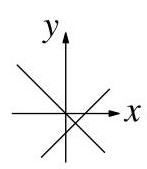
17.
正整数\( m, n \)和\( p \)满足方程\( {3m} + \frac{3}{n + \frac{1}{p}} = {17} \)。\( p \)的值是多少?
A 2 B 3 C 4 D 6 E 9
18.
两个圆\( {C}_{1} \)和\( {C}_{2} \)的圆心位于点(3,4),并且与第三个圆\( {C}_{3} \)相切。\( {C}_{3} \)的圆心位于点(0,0),半径为2。
两个圆\( {C}_{1} \)和\( {C}_{2} \)的半径之和是多少?
A 6 B 7 C 8 D 9 E 10
19.
字母\( p, q, r, s \)和\( t \)代表不同的正一位数,使得\( p - q = r \)且\( r - s = t \)。
\( t \)可能有多少种不同的取值?
A 6 B 5 C 4 D 3 E 2
20.
实数\( x \)和\( y \)满足方程\( {4}^{y} = \frac{1}{8{\left( \sqrt{2}\right) }^{x + 2}} \)和\( {9}^{x} \times {3}^{y} = 3\sqrt{3} \)。
\( {5}^{x + y} \)的值是多少?
A 5% B 5 C \( \sqrt{5} \) D \( \frac{1}{5} \) E \( \frac{1}{\sqrt{5}} \)
21.
当完全写出时,数字\( {\left( {10}^{2020} + {2020}\right) }^{2} \)共有4041位。
这个4041位数的各位数字之和是多少?
A 9 B 17 C 25 D 2048 E 4041
22.
一个周长为\( 4\mathrm{\;{cm}} \)的正方形可按第一图所示被分割成两个全等的直角三角形和两个全等的梯形,使得这四块可重排成第二图所示的矩形。
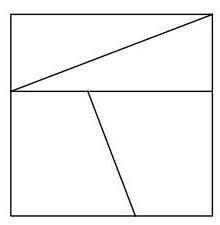
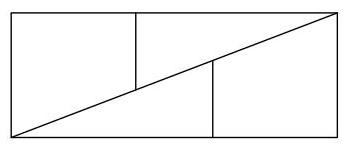
该矩形的周长是多少厘米?
A \( 2\sqrt{5} \) B \( 4\sqrt{2} \) C 5 D \( 4\sqrt{3} \) E \( 3\sqrt{7} \)
23.
函数\( f \)满足\( {y}^{3}f\left( x\right) = {x}^{3}f\left( y\right) \)且\( f\left( 3\right) \neq 0 \)。\( \frac{f\left( {20}\right) - f\left( 2\right) }{f\left( 3\right) } \)的值是多少?
A 6 B 20 C 216 D 296 E 2023
24.
在所示图中,\( M \)是\( {PQ} \)的中点。直线\( {PS} \)平分\( \angle {RPQ} \)并于\( {RQ} \)交于\( S \)。直线\( {ST} \)平行于\( {PR} \)并于\( {PQ} \)交于T。\( {PQ} \)的长度为12,\( {MT} \)的长度为1。角\( {SQT} \)为\( {120}^{ \circ } \)。
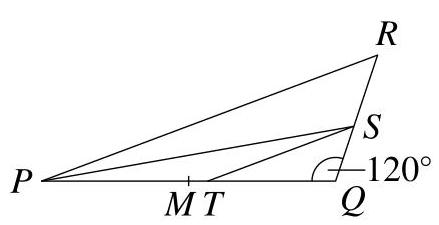
\( {SQ} \)的长度是多少?
A 2 B 3 C 3.5 D 4 E 5
25.
一个正\( m \)边形、一个正\( n \)边形和一个正\( p \)边形共用一个顶点,并且两两共享一条边,如图所示。
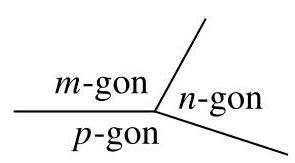
\( p \)的最大可能值是多少?
A 6 B 20 C 42 D 50 E 100