英国数学信托(United Kingdom Mathematics Trust)

高级数学挑战赛

由英国数学信托基金会(United Kingdom Mathematics Trust)主办，并获得支持

解决方案与调查

2021年11月

这些解答补充了同样可在线获取的简短解答。简短解答有时会省略细节。此处给出的解答是完整解答，如下文所述。在某些情况下，还提供了替代解法。此外，还有许多附加问题供进一步探究。我们欢迎对这些解答和附加问题提出意见。请发送至enquiry@ukmt.org.uk。

高级数学挑战赛(SMC)是一份选择题试卷。有时你可以通过从给定选项倒推，或证明其中四个选项不正确来找到正确答案。在SMC的情境下，这样做是明智的。

然而，这并不能提供一种完整的数学解释，倘若你仅拿到题目而没有任何备选答案，这样的解释便难以令人信服。因此，我们力求为每道题给出完整解答，每一步都加以说明(或偶尔留作练习)，且不预设任何给定选项为正确。我们希望这些解答能成为撰写完整数学问题解答的范例(例如在英国数学奥林匹克(British Mathematical Olympiad)、女子数学奥林匹克(Mathematical Olympiad for Girls)及类似竞赛中所需的那种书面解答)。

这些解答可在贵校或学院内自由使用。无需额外许可，您即可将其发布于仅限本校教职员工及学生访问的网站，在校内或学院内打印并分发纸质副本，并在课堂上使用。若您希望以其他方式使用，请先与我们联系。© UKMT 2021年11月

有关高级数学挑战赛(Senior Mathematical Challenge)的咨询请发送至:

SMC(高级数学挑战赛)，英国数学信托，数学学院，

利兹大学，利兹 LS2 9JT

& 0113 343 2339 enquiry@ukmt.org.uk www.ukmt.org.uk

---

\( \begin{array}{lllllllllllllllllllllllll} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & {10} & {11} & {12} & {13} & {14} & {15} & {16} & {17} & {18} & {19} & {20} & {21} & {22} & {23} & {24} & {25} \end{array} \)

---

SOLUTION

西塞莉在1939年迎来了她的21岁生日。因此\( {1939} - {21} = {1918} \)，她出生于1918年。

现在，\( {1918} + {100} = {2018} \)。

因此，西西莉的100岁生日是在2018年。

供探究

奥古斯都·德·摩根(Augustus De Morgan)出生于哪一年？

继续该序列，其中有多少项等于40？

SOLUTION

四舍五入后得到40的整数范围是35到44。

该范围内的素数为37、41和43。

因此，共有3个素数四舍五入后得到40。

供探究

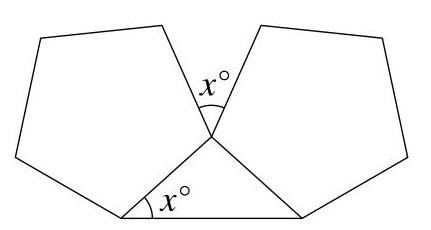
\( x \) 的值是多少？

解答

设 \( P, Q \) 和 \( R \) 为图中标出的点。正五边形的所有内角均为 \( {108}^{ \circ } \)。由于两个五边形全等，\( {PR} = {PQ} \)。因此 \( \angle {PRQ} = \angle {PQR} = {x}^{ \circ } \)。

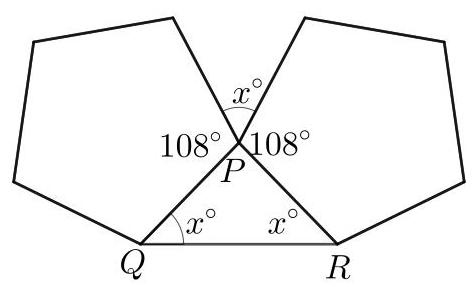
因为三角形内角和为 \( {180}^{ \circ } \)，由三角形 \( {PQR} \) 可得 \( {x}^{ \circ } + {x}^{ \circ } + \angle {QPR} = \) \( {180}^{ \circ } \)。因此 \( \angle {QPR} = {180}^{ \circ } - 2{x}^{ \circ } \)。

一点处的角度和为 \( {360}^{ \circ } \)。因此，由点 \( P \) 处的角度可得

\[ \left( {{180}^{ \circ } - 2{x}^{ \circ }}\right) + {108}^{ \circ } + {x}^{ \circ } + {108}^{ \circ } = {360}^{ \circ }. \]

即

\[ {396}^{ \circ } - {x}^{ \circ } = {360}^{ \circ }\text{.} \]

于是

\[ {x}^{ \circ } = {396}^{ \circ } - {360}^{ \circ } = {36}^{ \circ }. \]

探究

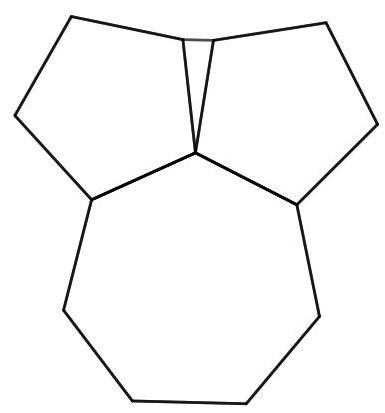
该三角形的内角分别是多少？

解答

我们有

\[ \left( {k \div {12}}\right) \div \left( {{15} \div k}\right) = \frac{k}{12} \div \frac{15}{k} \]

\[ = \frac{k}{12} \times \frac{k}{15} \]

\[ = \frac{k \times k}{{12} \times {15}} \]

\[ = \frac{{k}^{2}}{180}\text{.} \]

由此可得

\[ \left( {k \div {12}}\right) \div \left( {{15} \div k}\right) = {20} \Leftrightarrow \frac{{k}^{2}}{180} = {20} \]

\[ \Leftrightarrow {k}^{2} = {3600} \]

\[ \Leftrightarrow k = {60}\text{, as}k > 0\text{.} \]

60的各位数字之和为\( 6 + 0 = 6 \)。

供探究

(a) \( \left( {x \div 5}\right) \div \left( {5 \div x}\right) = 4 \) .

(b) \( \left( {x \div 2}\right) \div \left( {\left( {x \div {10}}\right) \div \left( {x \div 3}\right) }\right) = {15} \) .

这四个素数中最大的是哪一个？

SOLUTION

四个奇素数之和为大于2的偶数，因此不是素数。于是，这四个连续素数中必须包含唯一的偶素数2。

因此这四个连续素数是2、3、5和7。它们的和为17，是素数。这四个连续素数中最大的是7。

供探究

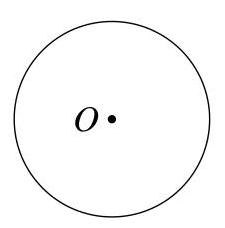
扇形\( {POQ},{QOR} \)与\( {ROP} \)的面积之比是多少？

解答

我们需要用到的关键事实有

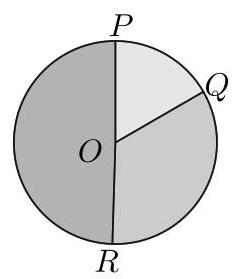
(a) 弧长与圆周长之比等于该弧所对圆心角与一整周角之比，

以及

(b) 扇形面积与圆面积之比等于该扇形圆心角与一整周角之比。

由(a)可知，\( {PQ},{QR} \) 与 \( {RP} \) 的弧长之比等于它们在圆心所对圆心角之比。

因此这些圆心角之比为 \( 1 : 2 : 3 \)。

同理，由(b)可知，扇形 \( {POQ},{QOR} \) 与 \( {ROP} \) 的面积之比等于它们圆心角之比。

因此扇形 \( {POQ},{QOR} \) 与 \( {ROP} \) 的面积之比为 \( 1 : 2 : 3 \)。评注

由基本事实(a)和(b)可推出

(c) 圆的弧长与圆周长之比等于该弧所对圆心角对应的扇形面积与圆面积之比。

另一种解法可直接基于这一事实。

探究

扇形 \( {QOR} \) 的面积是多少？

我们有

\[ {2}^{5000} = {\left( {2}^{5}\right) }^{1000} = {32}^{1000}, \]

\[ {3}^{4000} = {\left( {3}^{4}\right) }^{1000} = {81}^{1000}, \]

\[ {4}^{3000} = {\left( {4}^{3}\right) }^{1000} = {64}^{1000}\text{,} \]

并且

\[ {5}^{2000} = {\left( {5}^{2}\right) }^{1000} = {25}^{1000}. \]

由于 \( 6 < {25} < {32} < {64} < {81} \) ，因此 \( {6}^{1000} < {25}^{1000} < {32}^{1000} < {64}^{1000} < {81}^{1000} \) 。

所以 \( {6}^{1000} < {5}^{2000} < {2}^{5000} < {4}^{3000} < {3}^{4000} \) 。

因此，在给定的数中，最大的是 \( {3}^{4000} \) 。

供探究

(a) \( {2}^{7000} \) ，(b) \( {3}^{6000} \) ，(c) \( {4}^{5000} \) ，(d) \( {5}^{4000} \) ，(e) \( {6}^{3000} \) 。

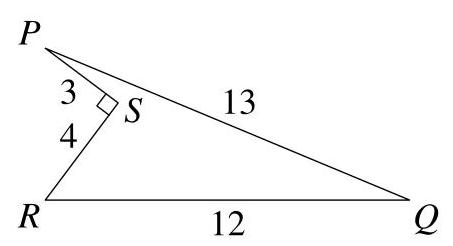
解答

对直角三角形 \( {PSR} \) 应用勾股定理(Pythagoras' Theorem)，我们有 \( P{R}^{2} = {3}^{2} + {4}^{2} = 9 + {16} = {25} \) 。因此 \( {PR} = 5 \) 。

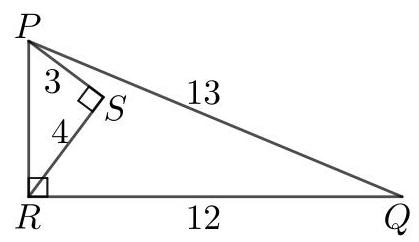
于是，在三角形 \( {PRQ} \) 中我们有

\[ P{Q}^{2} = {13}^{2} = {169} = {25} + {144} = {5}^{2} + {12}^{2} = P{R}^{2} + R{Q}^{2}. \]

因此，根据勾股定理的逆定理(converse of Pythagoras’ Theorem)， \( \angle {PRQ} = {90}^{ \circ } \) 。

因为\( \angle {PRQ} = {90}^{ \circ } \)，三角形\( {PRQ} \)的面积为\( \frac{1}{2}\left( {{RQ} \times {RP}}\right) = \frac{1}{2}\left( {{12} \times 5}\right) = {30} \)。同理，三角形\( {PSR} \)的面积为\( \frac{1}{2}\left( {{SP} \times {SR}}\right) = \frac{1}{2}\left( {3 \times 4}\right) = 6 \)。

四边形\( {PQRS} \)的面积等于三角形\( {PRQ} \)的面积减去三角形\( {PSR} \)的面积。因此\( {PQRS} \)的面积为\( {30} - 6 = {24} \)。

数字0只能与5配对。

数字1可以与4或9配对。如果1与4配对，则6必须与9配对；如果1与9配对，则6必须与4配对。

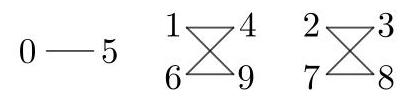
数字2可以与3或8配对。如果2与3配对，则7必须与8配对；如果2与8配对，则7必须与3配对。

这些可能性如上图所示。因此，完整的配对由以下两步决定:首先选择将1与4还是9配对，这有2种选择；然后选择将2与3还是8配对。

这些选择相互独立。因此共有\( 2 \times 2 = 4 \)种方法将这组数字分成五对，使得每对的和都是5的倍数。

供探究

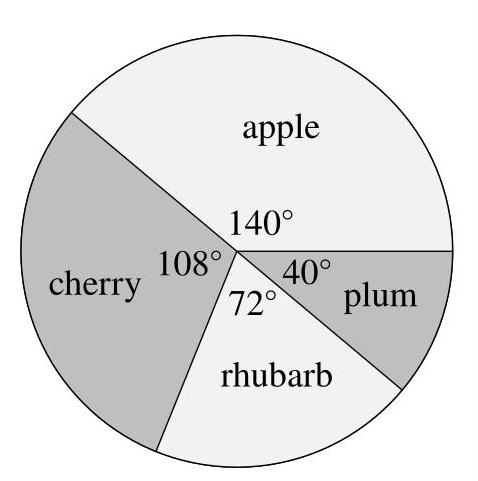
被调查者的最小可能人数是多少？

解答

假设共调查了\( p \)人。

所有角度之和为\( {360}^{ \circ } \)。因此，最喜欢苹果派的人数比例为\( \frac{140}{360} = \frac{7}{18} \)。于是选择苹果派的人数为\( \frac{7}{18}p \)，这是一个整数，故\( p \)是18的倍数。

同理，由于最喜欢樱桃派的人数比例为\( \frac{108}{360} = \frac{3}{10} \)，可推出\( p \)是10的倍数。

同样，由\( \frac{72}{360} = \frac{1}{5} \)和\( \frac{40}{360} = \frac{1}{9} \)可知，\( p \)也是5和9的倍数。

因此，\( p \)的最小可能值是18、10、5和9的最小公倍数，即90。故最少可能调查了90人。

深入探究

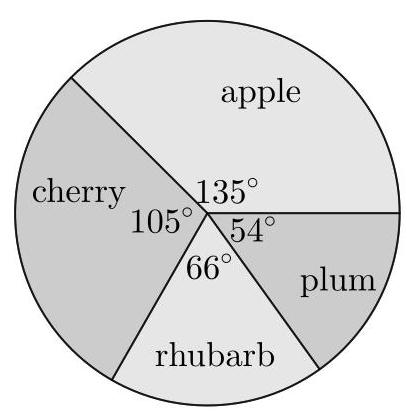
最少可能调查了多少人？

SOLUTION

该命题的反例是一个奇素数\( p \)，使得\( {p}^{2} - 2 \)不是奇素数。

3是奇素数，且\( {3}^{2} - 2 = 7 \)也是奇素数，故3不是反例。

5是奇素数，且\( {5}^{2} - 2 = {23} \)也是奇素数，故5不是反例。

7是奇素数，且\( {7}^{2} - 2 = {47} \)也是奇素数，故7不是反例。

9不是奇素数，故9不是反例。

11是奇素数，但\( {11}^{2} - 2 = {119} = 7 \times {17} \)不是奇素数，因此11是反例。

供探究

(a) 若\( p \)为素数，则\( {6p} + 1 \)亦为素数。

(b) 若\( p \)为整数且\( p > 1 \)，且\( {6p} + 1 \)为素数，则\( p \)亦为素数。

(c) 若\( p \)为素数，则\( {3}^{p} + {20} \)亦为素数。

(d) 若\( p \)为素数，则在\( p \)与\( p + {10} \)之间存在另一素数。

SOLUTION

当111除以\( N \)的余数为6时，有\( {111} = {QN} + 6 \)，其中\( Q \)为非负整数且\( 6 < N \)。换言之，\( N \)是\( {111} - 6 \)的因数且\( 6 < N \)。

现在\( {111} - 6 = {105} \)。105的素因数分解为\( 3 \times 5 \times 7 \)。因此\( {111} - 6 \)的因数为1,3,5,7,15,21,35和105。

在这8个因数中，除1,3,5外均大于6。

因此有5个正整数\( N \)使得111除以\( N \)的余数为6。供探究

SOLUTION

我们利用如下事实:若某一选项是其余四个选项的平均数，则它也是全部五个选项的平均数。请在问题13.2中验证这一事实。

五个选项所给数的平均数为

\[ \frac{\sqrt{2} + \sqrt{18} + \sqrt{200} + \sqrt{32} + \sqrt{8}}{5} = \frac{\sqrt{2} + 3\sqrt{2} + {10}\sqrt{2} + 4\sqrt{2} + 2\sqrt{2}}{5} \]

\[ = \left( \frac{1 + 3 + {10} + 4 + 2}{5}\right) \sqrt{2} \]

\[ = \left( \frac{20}{5}\right) \sqrt{2} \]

\[ = 4\sqrt{2} \]

\[ = \sqrt{32}\text{.} \]

因此正确选项是D。

供探究

(b) 由此证明该平均数是这些素数之一。

(c) 验证该平均数也是其余四个素数的平均数。

(b) 证明:若数\( p \)是四个数\( q, r, s \)和\( t \)的平均数，则\( p \)也是五个数\( p, q, r, s \)和\( t \)的平均数。

边长比为\( 5 : 4 \)的矩形尺寸为\( {5k}\mathrm{\;{cm}} \times {4k}\mathrm{\;{cm}} \)，其中\( k \)为某正数。由于我们要用\( 2\mathrm{\;{cm}} \times 3\mathrm{\;{cm}} \)个矩形无重叠地覆盖该矩形，\( k \)需为正整数。

该\( {5k}\mathrm{\;{cm}} \times {4k}\mathrm{\;{cm}} \)矩形的面积为\( \left( {{5k} \times {4k}}\right) {\mathrm{{cm}}}^{2} = {20}{k}^{2}{\mathrm{\;{cm}}}^{2} \)。\( 2\mathrm{\;{cm}} \times 3\mathrm{\;{cm}} \)个矩形的总面积为\( 6{\mathrm{\;{cm}}}^{2} \)。

因此\( {20}{k}^{2} \)需为6的倍数。满足此条件的最小正整数\( k \)为3。此时大矩形尺寸为\( {15}\mathrm{\;{cm}} \times {12}\mathrm{\;{cm}} \)，面积为\( \left( {{15} \times {12}}\right) {\mathrm{{cm}}}^{2} = {180}{\mathrm{\;{cm}}}^{2} \)。故所需\( 2\mathrm{\;{cm}} \times 3\mathrm{\;{cm}} \)矩形的最小数量为\( \frac{180}{6} = {30} \)，前提是能用30个\( 2\mathrm{\;{cm}} \times 3\mathrm{\;{cm}} \)矩形覆盖\( {15}\mathrm{\;{cm}} \times {12}\mathrm{\;{cm}} \)。

为完成本题，需证明这是可行的。

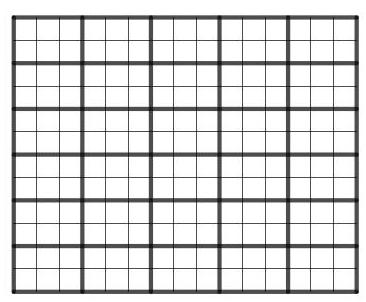
右图展示了一种可行方案。

因此，所需\( 2\mathrm{\;{cm}} \times 3\mathrm{\;{cm}} \)矩形的最小数量为30。

供探究

首先注意，由于骰子颜色不同，即使总和为10，只要某颗骰子掷出的数字不同，就算作不同结果。例如

红:6 蓝:3 黄:1

与以下结果视为不同

红:6 蓝:1 黄:3。

若三个数字各不相同，则先选哪颗骰子掷出第一个数字有3种选择，再选哪颗骰子掷出第二个数字有2种选择，最后一颗骰子只能掷出剩下的数字，共\( 3 \times 2 \times 1 = 6 \)种排列。

可以验证，当有两个数字相同时，共有3种不同方式。

不可能出现三个数字相同且总和为10的情况。

为求解此题，我们在下表中列出所有三颗骰子掷出总和为10的可能组合，并在每行给出这三个数字在三颗骰子间排列的不同方式数量。

分数	10. 方法
6, 3, 1	6
6, 2, 2	3
5, 4, 1	6
5, 3, 2	6
4,4,2	3
4,3,3	3

因此，使总和为10的不同方式共有\( 6 + 3 + 6 + 6 + 3 + 3 = {27} \)种。供探究

你注意到答案有什么规律？

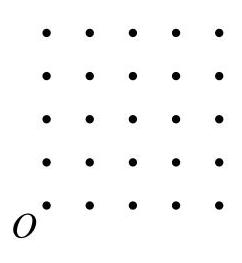
琳达可以画多少条这样的直线？

在右侧图中，实线经过\( O \)且恰好经过另一个点，虚线经过\( O \)且至少经过另外两个点。

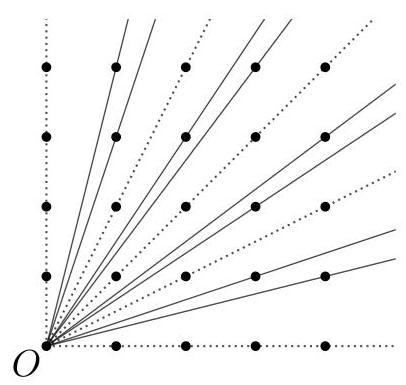
每个点都有一条直线经过，因此所有可能的直线均已考虑。

实线即为琳达可以画的直线。因此我们看到琳达可以画8条直线。

[注:由于图形关于左下到右上的对角线对称，实际上只需画出图中一半的直线即可。]

供探究

娜奥米想画一条直线，使其经过左下角的点且恰好经过另一个点。

Naomi可以画多少条这样的直线？

Olivia想画一条直线，这条直线经过左下角的点，并且恰好还经过另一个点。

Olivia可以画多少条这样的直线？

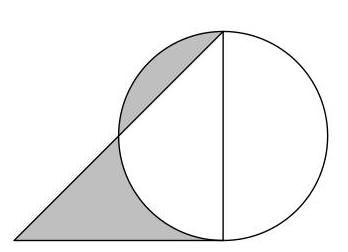
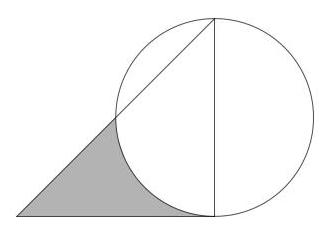
阴影部分的面积是多少？

\( \mathrm{E}\left( {\sqrt{2} - 1}\right) \pi {r}^{2} \)

SOLUTION

设\( O \)为圆心，\( P, Q, R \)和\( S \)为图中标出的点。

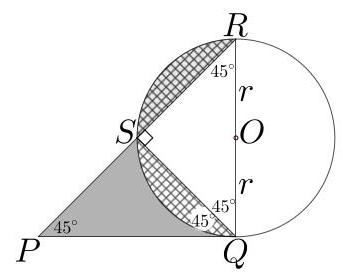
因为\( {PQR} \)是一个直角等腰三角形，所以\( \angle {PRQ} = \)\( \angle {RPQ} = {45}^{ \circ } \)，且\( {PQ} = {QR} = {2r} \)。

因为半圆上的圆周角是直角[这是泰勒斯定理(Thales' theorem)]，所以\( \angle {RSQ} = {90}^{ \circ } \)。因此，由于三角形内角和为\( {180}^{ \circ } \)，我们得到\( \angle {RQS} = {45}^{ \circ } \)。

因此我们得到\( \angle {SRQ} = {45}^{ \circ } = \angle {SQR} \)。于是\( {SQ} = {SR} \)。

因为\( {SQ} = {SR} \)，这些直线截出的圆弓形(图中以阴影线表示)是全等的，因此它们的面积相等。

于是阴影部分的面积与三角形\( {PQS} \)的面积相同。

\( {PQS} \)是一个直角等腰三角形，斜边\( {PQ} \)的长度为\( {2r} \)。因此三角形\( {PQS} \)的面积为\( {r}^{2} \)。

因此阴影部分的面积为\( {r}^{2} \)。

供探究

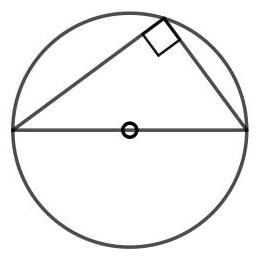
阴影部分的面积是多少？17.3 请给出泰勒斯定理(Thales' theorem)的证明:

半圆上的圆周角是直角。

解答

首先注意到，由于\( \frac{p!}{q!} = {840} \)，因此\( p! > q \)！从而\( p > q \)。因此

\[ \frac{p!}{q!} = \frac{1 \times 2 \times \cdots \times q \times \left( {q + 1}\right) \times \cdots \times p}{1 \times 2 \times \cdots \times q} = \left( {q + 1}\right) \times \left( {q + 2}\right) \times \cdots \times \left( {p - 1}\right) \times p. \]

于是\( {840} = \frac{p!}{q!} \)是连续整数\( q + 1, q + 2,\ldots , p - 1, p \)的乘积，其中\( p \leq 9 \)。由于840不是\( 9, p \neq 9 \)的倍数，而840是\( 7, p \geq 7 \)的倍数。

现在\( 5 \times 6 \times 7 \times 8 = {1680} > {840} \)，而\( 6 \times 7 \times 8 = {336} < {840} \)。因此840不是以8为最大连续整数的乘积。

我们推断\( p = 7 \)。现在可直接验证

\[ {840} = 4 \times 5 \times 6 \times 7 = \frac{7!}{3!}. \]

因此\( p = 7 \)且\( q = 3 \)。于是\( p + q = 7 + 3 = {10} \)。

供探究

\[ \frac{p!}{q!} = {2730} \]

\[ \frac{p!}{q!} = {253}? \]

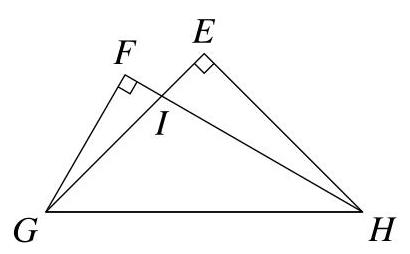
三角形\( {IFG} \)的面积与三角形\( {IEH} \)的面积之比是多少？

我们假设所选单位使得\( {GH} \)的长度为1。

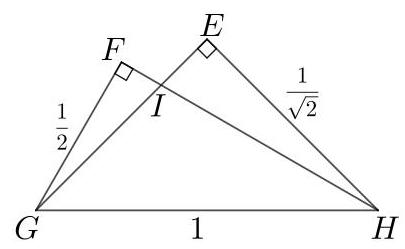
因为\( {FGH} \)是一个\( {60}^{ \circ },{30}^{ \circ },{90}^{ \circ } \)三角形，所以\( {FG} \)的长度为\( \frac{1}{2} \)。

由于\( {EGH} \)是一个直角等腰三角形，因此\( {EH} \)的长度为\( \frac{1}{\sqrt{2}} \)。

在三角形\( {IFG} \)和\( {IEH} \)中，我们有

\[ \angle {GFI} = \angle {HEI} = {90}^{ \circ } \]

以及

\[ \angle {GIF} = \angle {HIE}\text{(vertically opposite angles).} \]

因为这两个三角形的内角和均为\( {180}^{ \circ } \)，所以

\[ \angle {FGI} = \angle {EHI}\text{.} \]

因此，三角形\( {IFG} \)和\( {IEH} \)相似。

相似三角形的面积之比等于对应边长度之比的平方。因此

\[ \text{area of}{IFG} : \text{area of}{IEH} = F{G}^{2} : E{H}^{2} \]

\[ = {\left( \frac{1}{2}\right) }^{2} : {\left( \frac{1}{\sqrt{2}}\right) }^{2} \]

\[ = \frac{1}{4} : \frac{1}{2} \]

\[ = 1 : 2\text{.} \]

供探究

(b) 已知\( {GH} \)的长度为1，求三角形\( {IFG} \)和\( {IEH} \)的面积。

(c) 由此验证三角形\( {IFG} \)与\( {IEH} \)的面积之比为\( 1 : 2 \)。

迪娜在超越劳拉前跑了多少米？

假设迪娜在超越劳拉时跑了\( d \)米。由于劳拉提前\( s \)米起跑，此时劳拉已跑\( d - s \)米。

因为迪娜超越劳拉时两人已奔跑相同时间，此时两人所跑距离的比值等于其速度的比值。即

\[ d : d - s = n : 1 \]

由此可得

\[ \frac{d}{d - s} = \frac{n}{1} \]

因此

\[ d = n\left( {d - s}\right) . \]

最后一个方程可整理为

\[ {ns} = d\left( {n - 1}\right) \text{.} \]

所以

\[ d = \frac{ns}{n - 1}. \]

深入探究

数\( m \)和\( k \)满足方程\( {2}^{m} + {2}^{k} = p \)和\( {2}^{m} - {2}^{k} = q \)。

用\( p \)和\( q \)表示\( {2}^{m + k} \)的值是多少？

解答

我们有

\[ {2}^{m} + {2}^{k} = p \tag{1} \]

且

\[ {2}^{m} - {2}^{k} = q \tag{2} \]

将方程(1)与方程(2)相加，我们得到

\[ 2\left( {2}^{m}\right) = p + q \]

因此

\[ {2}^{m} = \frac{p + q}{2} \tag{3} \]

用方程(1)减去方程(2)，我们得到

\[ 2\left( {2}^{k}\right) = p - q \]

因此

\[ {2}^{k} = \frac{p - q}{2}. \tag{4} \]

因此，由(3)和(4)得

\[ {2}^{m + k} = {2}^{m} \times {2}^{k} \]

\[ = \left( \frac{p + q}{2}\right) \times \left( \frac{p - q}{2}\right) \]

\[ = \frac{\left( {p + q}\right) \left( {p - q}\right) }{4} \]

\[ = \frac{{p}^{2} - {q}^{2}}{4}\text{.} \]

供探究

\[ {2}^{a + b} = r \]

且

\[ {2}^{a - b} = s. \]

用\( r \)和\( s \)表示\( {2}^{a} + {2}^{b} \)。

该三角形的面积是多少？

设\( P, Q \)和\( R \)为三角形的顶点，设\( O \)为圆心，如图所示。

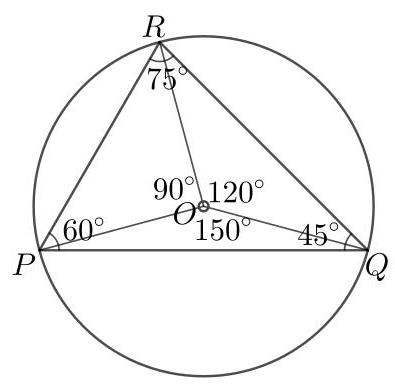
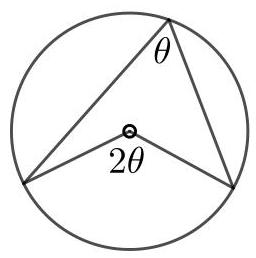
圆心所对的弧心角是圆周角的两倍。因此

\[ \angle {QOR} = {120}^{ \circ }\text{,} \]

\[ \angle {ROP} = {90}^{ \circ } \]

且

\[ \angle {POQ} = {150}^{ \circ }\text{.} \]

我们用记号\( \left\lbrack {XYZ}\right\rbrack \)表示三角形\( {XYZ} \)的面积。

利用边长为\( a \)和\( b \)且夹角为\( \theta \)的三角形面积公式\( \frac{1}{2}{ab}\sin \theta \)，我们有

\[ \left\lbrack {QOR}\right\rbrack = \frac{1}{2}\left( {{OQ} \times {OR}}\right) \sin {120}^{ \circ } = \frac{1}{2}\left( {2 \times 2}\right) \frac{\sqrt{3}}{2} = \sqrt{3}\text{,} \]

\[ \left\lbrack {ROP}\right\rbrack = \frac{1}{2}\left( {{OR} \times {OP}}\right) \sin {90}^{ \circ } = \frac{1}{2}\left( {2 \times 2}\right) = 2 \]

且

\[ \left\lbrack {POQ}\right\rbrack = \frac{1}{2}\left( {{OP} \times {OQ}}\right) \sin {150}^{ \circ } = \frac{1}{2}\left( {2 \times 2}\right) \frac{1}{2} = 1. \]

因此

\[ \left\lbrack {PQR}\right\rbrack = \left\lbrack {QOR}\right\rbrack + \left\lbrack {ROP}\right\rbrack + \left\lbrack {POQ}\right\rbrack = \sqrt{3} + 2 + 1 = 3 + \sqrt{3}. \]

供探究

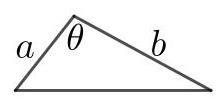
我们有

\[ \left( {{x}^{2} - {4x} + 3}\right) \left( {{x}^{2} + {4x} + 3}\right) = \left( {\left( {{x}^{2} + 3}\right) - {4x}}\right) \left( {\left( {{x}^{2} + 3}\right) + {4x}}\right) \]

\[ = {\left( {x}^{2} + 3\right) }^{2} - {\left( 4x\right) }^{2} \]

\[ = {x}^{4} + 6{x}^{2} + 9 - {16}{x}^{2} \]

\[ = {x}^{4} - {10}{x}^{2} + 9 \]

\[ = {\left( {x}^{2} - 5\right) }^{2} - {16}\text{.} \]

对于每一个实数\( x,{\left( {x}^{2} - 5\right) }^{2} \geq 0 \)，因此\( {\left( {x}^{2} - 5\right) }^{2} - {16} \geq - {16} \)。

现在，当\( x = \sqrt{5},{\left( {x}^{2} - 5\right) }^{2} - {16} = {0}^{2} - {16} = - {16} \)。

由此可知，\( \left( {{x}^{2} - {4x} + 3}\right) \left( {{x}^{2} + {4x} + 3}\right) \)的最小值为-16。

供探究

\[ {x}^{4} - 8{x}^{2} + {12} = {\left( {x}^{2} + a\right) }^{2} + b\text{, for all real numbers}x\text{.} \]

(b) 因此求出\( {x}^{4} - 8{x}^{2} + {12} \)的最小值。

\[ {x}^{4} + 8{x}^{2} + {12} = {\left( {x}^{2} + a\right) }^{2} + b\text{, for all real numbers}x\text{.} \]

(b) 因此求出\( {x}^{4} + 8{x}^{2} + {12} \)的最小值。

注

如果你已学过微分学(differential calculus)，就会知道多项式的最小值可用微积分求得。在此情形下，请验证使用微积分得到多项式\( \left( {{x}^{2} - {4x} + 3}\right) \left( {{x}^{2} + {4x} + 3}\right) \)的最小值为-16。

同时，用微积分解答问题23.1和23.2。

Derin独自完成该任务需多少分钟？A 21 B 28 C 35 D 48 E 105 解答

设Saba、Rayan和Derin独自完成任务分别需\( s, r \)、\( d \)分钟。

则Saba每分钟完成任务的\( \frac{1}{s} \)，Rayan每分钟完成\( \frac{1}{r} \)，Derin每分钟完成\( \frac{1}{d} \)。因此三人一起每分钟完成\( \frac{1}{s} + \frac{1}{r} + \frac{1}{d} \)。由于三人一起工作需5分钟完成全部任务，

一起工作时，

\[ \frac{1}{s} + \frac{1}{r} + \frac{1}{d} = \frac{1}{5} \]

同理，Saba与Derin一起工作需7分钟完成任务，

\[ \frac{1}{s} + \frac{1}{d} = \frac{1}{7} \]

同样，Rayan与Derin一起工作需15分钟完成任务，

\[ \frac{1}{r} + \frac{1}{d} = \frac{1}{15} \]

于是我们有

\[ \frac{1}{d} = \left( {\frac{1}{s} + \frac{1}{d}}\right) + \left( {\frac{1}{r} + \frac{1}{d}}\right) - \left( {\frac{1}{s} + \frac{1}{r} + \frac{1}{d}}\right) \]

\[ = \frac{1}{7} + \frac{1}{15} - \frac{1}{5} \]

\[ = \frac{15}{105} + \frac{7}{105} - \frac{21}{105} \]

\[ = \frac{1}{105}\text{.} \]

因此Derin独自完成任务需105分钟。

供探究

(b) Saba独自完成这项任务需要多少分钟？

阴影部分的面积是多少？

解答

评注

这个问题有多种解法。我们给出一种计算量较少但需要大量图形性质的解法。请在问题25.1和25.2中验证这些性质。

另外三种解法在问题25.3、25.4和25.5中给出。

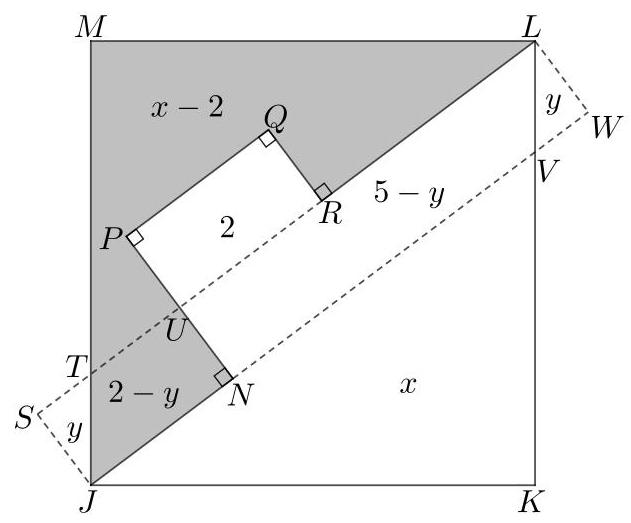
我们按图所示标记各点。选择点\( S \)和\( W \)使得\( {SJWL} \)为矩形。

阴影区域为多边形\( {JNPQRLM} \)。我们用\( \left\lbrack {JNPQRLM}\right\rbrack \)表示该多边形的面积，其他多边形面积用类似记号。

在矩形\( {SJWL} \)中，我们有\( {JW} = 7 \)和\( {WL} = 1 \)。因此，对三角形\( {JWL} \)应用勾股定理(Pythagoras’ Theorem)，得\( J{L}^{2} = {7}^{2} + {1}^{2} = {50} \)。故\( {JL} = \sqrt{50} = 5\sqrt{2} \)。由于正方形对角线\( {JKLM} \)的长度为\( 5\sqrt{2} \)，可知正方形边长为5。因此\( \left\lbrack {JKLM}\right\rbrack = {5}^{2} = {25} \)。(请在问题25.1中验证所有这些事实。)

三角形\( {JKV} \)与\( {LMT} \)全等。设\( x \)为这两个三角形的公共面积。同样，三角形\( {JTS} \)与\( {LVW} \)全等。设\( y \)为这两个三角形的公共面积。因此图中各多边形的面积如图所示。(请在问题25.2中验证所有这些事实。)

我们有

\[ \left\lbrack {JKLM}\right\rbrack = \left\lbrack {JKV}\right\rbrack + \left\lbrack {LMT}\right\rbrack + \left\lbrack {SJWL}\right\rbrack - \left\lbrack {JTS}\right\rbrack - \left\lbrack {LVW}\right\rbrack , \]

因此

\[ {25} = {2x} + 7 - {2y}\text{.} \]

故

\[ {2x} - {2y} = {25} - 7 = {18}, \]

因此

\[ x - y = 9\text{.} \]

由此可得

\[ \left\lbrack {JNPQRLM}\right\rbrack = \left\lbrack {TUPQRLM}\right\rbrack + \left\lbrack {JNUT}\right\rbrack = \left( {x - 2}\right) + \left( {2 - y}\right) = x - y = 9. \]

注:在下列问题中，我们使用与上述解答相同的记号。

供探究

(b) 解释为何由对角线\( {JL} \)长度为\( 5\sqrt{2} \)可推出正方形\( {JKLM} \)的边长为5。

(b) 推导出图中多边形的面积如所示。25.3

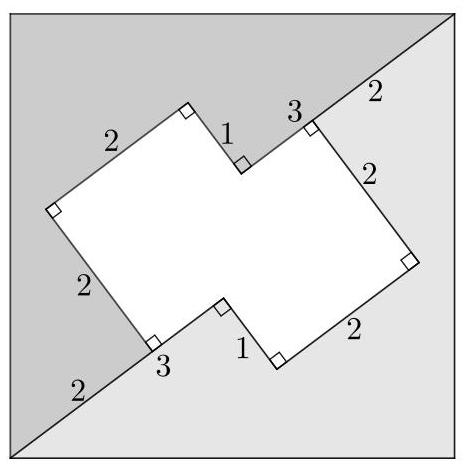
上图中浅阴影区域被绘制为与待求面积的区域全等。

(a) 求图中未阴影区域的面积。

(b) 利用正方形面积为25，求出每个阴影区域的面积。

(b) 推导出\( {LV} \)的长度为\( \frac{5}{4} \)，且\( {VK} \)的长度为\( \frac{15}{4} \)。

(c) 利用这些长度求出\( x \)和\( y \)的值。

从而验证\( x - y = 9 \)。

(a) 通过考虑线段\( {JN},{NP},{PQ},{QR} \)和\( {RL} \)在\( {JK} \)和\( {JM} \)上的投影，证明两者

\[ 7\cos \theta - \sin \theta = {JK} \]

和

\[ 7\sin \theta + \cos \theta = {JM}. \]

(b) 利用\( {JK} = {JM} \)这一事实，推导出\( \sin \theta = \frac{3}{4}\cos \theta \)。进而求出\( \cos \theta \)和\( \sin \theta \)的值。

(c) 利用\( \cos \theta \)和\( \sin \theta \)的值计算多边形\( {JNPQRLM} \)的面积。