8.6 The Trapezium Rule - 教材内容

基本概念

学习目标：掌握梯形法则的数值积分方法，用于近似计算曲线下面积。

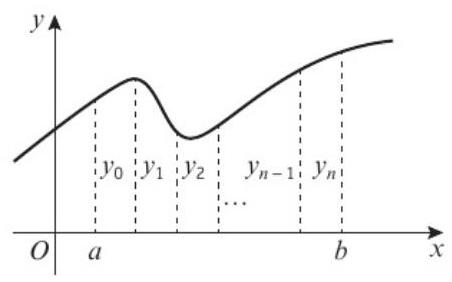
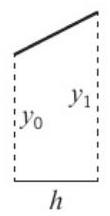
梯形法则：\(\int_a^b y dx \approx \frac{1}{2}h[y_0 + 2(y_1 + y_2 + ... + y_{n-1}) + y_n]\)

其中：\(h = \frac{b-a}{n}\)，\(y_i = f(a + ih)\)

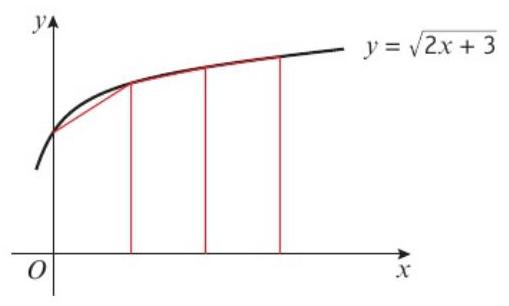
重要：当无法用代数方法积分函数时，可以使用数值方法来近似计算曲线下的面积。

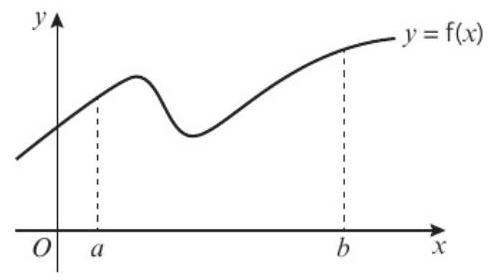
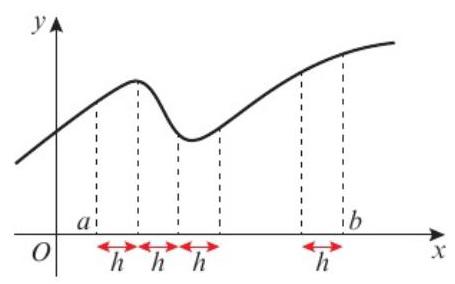
图1：梯形法则基本概念 - 将曲线下面积分割成n个梯形

公式推导

推导过程：将曲线下面积分割成n个相等的梯形，每个梯形宽度为h。

图2：梯形分割示意图 - 计算每个x点的y值

分割区间：将[a,b]分成n个相等区间，每个宽度h = (b-a)/n
计算x值：x = a, a+h, a+2h, ..., b
计算y值：y = f(x) 在每个x点的值
标记y值：y₀, y₁, y₂, ..., yₙ
计算梯形面积：每个梯形面积 = ½(y₀ + y₁)h
求和：总面积 ≈ ½h[y₀ + 2(y₁ + y₂ + ... + yₙ₋₁) + yₙ]

图3：多个梯形组合近似曲线下面积

图4：单个梯形面积计算

Example 10 - 梯形法则应用

题目：

Use the trapezium rule with a) 4 strips b) 8 strips to estimate the area under the curve with equation \(y = \sqrt{2x + 3}\) between the lines \(x = 0\) and \(x = 2\).

解：

a) 4个梯形：每个梯形宽度 h = (2-0)/4 = 0.5
计算y值：y = √(2x + 3)

x	0	0.5	1	1.5	2
y = √(2x + 3)	1.732	2	2.236	2.449	2.646

Area = ½ × 0.5 × (1.732 + 2(2 + 2.236 + 2.449) + 2.646)

= ½ × 0.5 × 17.748 = 4.437 或 4.44

b) 8个梯形：每个梯形宽度 h = (2-0)/8 = 0.25

x	0	0.25	0.5	0.75	1	1.25	1.5	1.75	2
y = √(2x + 3)	1.732	1.871	2	2.121	2.236	2.345	2.449	2.550	2.646

Area = ½ × 0.25 × (1.732 + 2(1.871 + 2 + 2.121 + 2.236 + 2.345 + 2.449 + 2.550) + 2.646)

= ½ × 0.25 × 35.522 = 4.44025 或 4.44

图5：Example 10 - y = √(2x + 3) 曲线图

精度分析

实际面积：在这个例子中，实际面积是4.441368...，可以看到增加梯形数量（减少宽度）应该提高近似的精度。

曲线形状：曲线y = √(2x + 3)是凹的（向下弯曲），所以每个梯形完全在曲线下方。梯形法则在这种情况下会给出低估值。

重要提示

Hint：对于n个梯形，将有n+1个x值和n+1个y值。

Watch out：在考试中使用梯形法则时，要显示x_i和y_i的值以及如何代入公式。

计算器：图形计算器可以用来计算定积分。计算器通常使用与梯形法则略有不同的方法，通常更准确。

解题策略

制作表格：列出所有x和y值
应用公式：使用梯形法则公式
检查计算：确保计算正确
分析精度：考虑曲线形状对精度的影响