在实际应用中,我们经常需要根据给定的概率条件来求解正态分布的未知参数μ(均值)和σ(标准差)。这是统计学中参数估计的重要技能。
In practical applications, we often need to solve for unknown parameters μ (mean) and σ (standard deviation) of a normal distribution based on given probability conditions. This is an important skill in parameter estimation in statistics.
基本思路:使用标准化公式 Z = (X - μ)/σ 将问题转化为标准正态分布问题
Basic approach: Use the standardization formula Z = (X - μ)/σ to transform the problem into a standard normal distribution problem
当正态分布的方差已知,但均值未知时,我们可以通过给定的概率条件来求解均值。
When the variance of a normal distribution is known but the mean is unknown, we can solve for the mean through given probability conditions.
随机变量X ~ N(μ, 3²)
Random variable X ~ N(μ, 3²)
已知P(X > 20) = 0.20,求μ的值
Given P(X > 20) = 0.20, find the value of μ
解 / Solution:
1. 使用标准化公式:Z = (X - μ)/σ
1. Use standardization formula: Z = (X - μ)/σ
2. P(X > 20) = 0.20 → P(Z > (20 - μ)/3) = 0.20
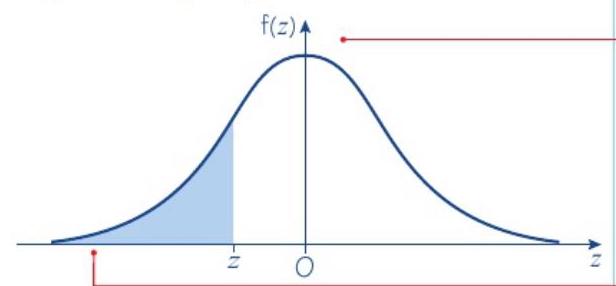
3. 绘制Z的图表,p = 0.20
3. Draw a diagram for Z, p = 0.20
4. 由于P(Z > z) = 0.20 < 0.5,所以z > 0
4. Since P(Z > z) = 0.20 < 0.5, so z > 0
5. 在百分比点表中查找p = 0.20对应的z值
5. Look up the z-value corresponding to p = 0.20 in the percentage points table
6. z = 0.8416
7. 因此:(20 - μ)/3 = 0.8416
7. Therefore: (20 - μ)/3 = 0.8416
8. 解得:μ = 20 - 3 × 0.8416 = 17.4752
8. Solving: μ = 20 - 3 × 0.8416 = 17.4752
答案:μ = 17.5 (3 s.f.)
当正态分布的均值已知,但标准差未知时,我们可以通过给定的概率条件来求解标准差。
When the mean of a normal distribution is known but the standard deviation is unknown, we can solve for the standard deviation through given probability conditions.
机器制造的金属板宽度X ~ N(50, σ²),单位为厘米
A machine makes metal sheets with width X ~ N(50, σ²) in centimeters
a) 已知P(X < 46) = 0.2119,求σ的值
a) Given P(X < 46) = 0.2119, find the value of σ
b) 求宽度的第90百分位数
b) Find the 90th percentile of the widths
解 / Solution:
a) 求σ的值
a) Find the value of σ
1. P(X < 46) = 0.2119
2. 使用标准化公式:P(Z < (46 - 50)/σ) = 0.2119
2. Use standardization formula: P(Z < (46 - 50)/σ) = 0.2119
3. P(Z < -4/σ) = 0.2119
4. 绘制Z的图表,p = 0.2119
4. Draw a diagram for Z, p = 0.2119
5. 由于P(Z < z) = 0.2119 < 0.5,所以z < 0
5. Since P(Z < z) = 0.2119 < 0.5, so z < 0
6. 使用对称性:P(Z < -0.80) = 0.2119
6. Use symmetry: P(Z < -0.80) = 0.2119
7. 因此:-4/σ = -0.80
7. Therefore: -4/σ = -0.80
8. 解得:σ = 4/0.80 = 5
8. Solving: σ = 4/0.80 = 5
答案:σ = 5
b) 求第90百分位数
b) Find the 90th percentile
1. 设第90百分位数为a,则P(X < a) = 0.9
1. Let the 90th percentile be a, then P(X < a) = 0.9
2. 现在X ~ N(50, 5²)
2. Now X ~ N(50, 5²)
3. P(Z < (a - 50)/5) = 0.9
4. 在主表中查找0.9对应的z值
4. Look up the z-value corresponding to 0.9 in the main table
5. z = 1.2816
6. 因此:(a - 50)/5 = 1.2816
6. Therefore: (a - 50)/5 = 1.2816
7. 解得:a = 50 + 5 × 1.2816 = 56.408
7. Solving: a = 50 + 5 × 1.2816 = 56.408
答案:a = 56.4 cm (3 s.f.)
当正态分布的均值和标准差都未知时,我们需要两个独立的概率条件来建立方程组求解。
When both the mean and standard deviation of a normal distribution are unknown, we need two independent probability conditions to establish a system of equations for solving.
随机变量X ~ N(μ, σ²)
Random variable X ~ N(μ, σ²)
已知P(X > 35) = 0.025 和 P(X < 15) = 0.1469
Given P(X > 35) = 0.025 and P(X < 15) = 0.1469
求μ和σ的值
Find the values of μ and σ
解 / Solution:
1. 建立两个方程:
1. Establish two equations:
P(X > 35) = 0.025 → P(Z > (35 - μ)/σ) = 0.025
P(X < 15) = 0.1469 → P(Z < (15 - μ)/σ) = 0.1469
2. 查找对应的z值:
2. Find corresponding z-values:
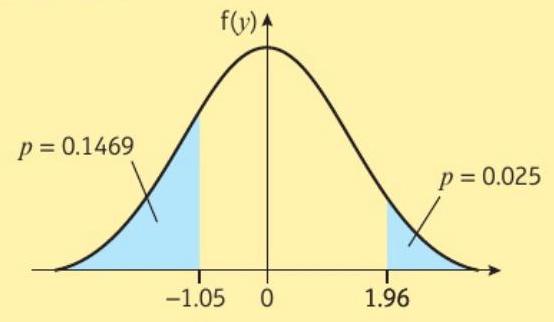
P(Z > z₁) = 0.025 → z₁ = 1.96 (从百分比点表)
P(Z > z₁) = 0.025 → z₁ = 1.96 (from percentage points table)
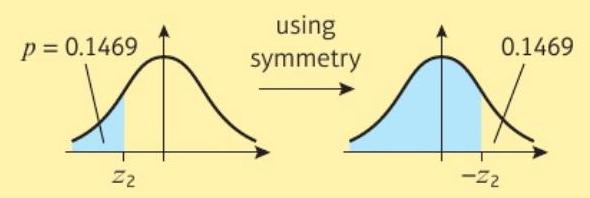
P(Z < z₂) = 0.1469 → z₂ = -1.05 (使用对称性)
P(Z < z₂) = 0.1469 → z₂ = -1.05 (using symmetry)
3. 建立方程组:
3. Establish system of equations:
(35 - μ)/σ = 1.96 → 1.96σ + μ = 35 ... (1)
(15 - μ)/σ = -1.05 → -1.05σ + μ = 15 ... (2)
4. 解方程组:
4. Solve the system:
(1) - (2): 3.01σ = 20
σ = 20/3.01 = 6.6445...
5. 代入(1)式:
5. Substitute into equation (1):
μ = 35 - 1.96 × 6.6445... = 21.976...
答案:σ = 6.64, μ = 22.0 (3 s.f.)
求解未知参数的标准步骤:
Standard steps for finding unknown parameters:
-
识别问题类型 / Identify problem type:
- 只求μ(σ已知)/ Only find μ (σ known)
- 只求σ(μ已知)/ Only find σ (μ known)
- 同时求μ和σ / Find both μ and σ
-
建立方程 / Establish equations:
- 使用标准化公式Z = (X - μ)/σ
- Use standardization formula Z = (X - μ)/σ
- 将概率条件转化为标准正态分布问题
- Transform probability conditions into standard normal distribution problems
-
查找z值 / Find z-values:
- 使用百分比点表或主表
- Use percentage points table or main table
- 注意z值的符号
- Pay attention to the sign of z-values
-
求解参数 / Solve for parameters:
- 单个参数:直接求解
- Single parameter: solve directly
- 两个参数:建立方程组求解
- Two parameters: establish system of equations and solve
-
验证答案 / Verify answer:
- 检查答案的合理性
- Check reasonableness of answers
- 代入原条件验证
- Substitute back into original conditions to verify
当给定的概率条件具有对称性时,可以利用对称性简化计算:
When given probability conditions have symmetry, we can use symmetry to simplify calculations:
• 如果P(X > a) = P(X < b) = p,则μ = (a + b)/2
• If P(X > a) = P(X < b) = p, then μ = (a + b)/2
• 利用对称性可以快速确定均值的位置
• Using symmetry can quickly determine the position of the mean
随机变量X ~ N(μ, σ²)
Random variable X ~ N(μ, σ²)
已知P(X > 15) = 0.20 和 P(X < 9) = 0.20
Given P(X > 15) = 0.20 and P(X < 9) = 0.20
求μ和σ的值
Find the values of μ and σ
解 / Solution:
1. 由于P(X > 15) = P(X < 9) = 0.20,具有对称性
1. Since P(X > 15) = P(X < 9) = 0.20, there is symmetry
2. 利用对称性:μ = (15 + 9)/2 = 12
2. Use symmetry: μ = (15 + 9)/2 = 12
3. 现在求σ:P(X > 15) = 0.20
3. Now find σ: P(X > 15) = 0.20
4. P(Z > (15 - 12)/σ) = 0.20
5. P(Z > 3/σ) = 0.20
6. 3/σ = 0.8416
7. σ = 3/0.8416 = 3.57
答案:μ = 12, σ = 3.57 (3 s.f.)
分位数问题是指给定某个百分位数,求对应的参数值。这类问题在实际应用中很常见。
Quantile problems refer to finding corresponding parameter values given a certain percentile. These problems are common in practical applications.
随机变量X ~ N(μ, σ²)
Random variable X ~ N(μ, σ²)
X的下四分位数是25,上四分位数是45
The lower quartile of X is 25 and the upper quartile is 45
求μ和σ的值
Find the values of μ and σ
解 / Solution:
1. 下四分位数:P(X < 25) = 0.25
1. Lower quartile: P(X < 25) = 0.25
2. 上四分位数:P(X < 45) = 0.75
2. Upper quartile: P(X < 45) = 0.75
3. 建立方程组:
3. Establish system of equations:
P(Z < (25 - μ)/σ) = 0.25 → (25 - μ)/σ = -0.6745
P(Z < (45 - μ)/σ) = 0.75 → (45 - μ)/σ = 0.6745
4. 解方程组:
4. Solve the system:
(25 - μ)/σ = -0.6745 → -0.6745σ + μ = 25 ... (1)
(45 - μ)/σ = 0.6745 → 0.6745σ + μ = 45 ... (2)
5. (2) - (1): 1.349σ = 20
6. σ = 20/1.349 = 14.83
7. μ = 45 - 0.6745 × 14.83 = 35.0
答案:μ = 35.0, σ = 14.8 (3 s.f.)
-
方程建立错误 / Incorrect equation establishment: 忘记使用标准化公式
Forgetting to use the standardization formula -
z值符号错误 / Incorrect z-value signs: 没有正确判断z值的正负号
Not correctly determining the sign of z-values -
方程组求解错误 / Incorrect system solving: 在求解两个参数时出现计算错误
Calculation errors when solving for two parameters -
单位问题 / Unit issues: 忘记考虑单位的一致性
Forgetting to consider unit consistency -
近似值选择 / Approximation selection: 当概率值不在表中时,没有选择最接近的值
Not choosing the closest value when probability is not in the table
在求解未知参数时,一定要确保有足够的信息来唯一确定参数值。对于两个未知参数,通常需要两个独立的概率条件。
When solving for unknown parameters, make sure there is sufficient information to uniquely determine the parameter values. For two unknown parameters, two independent probability conditions are usually needed.
寻找未知参数μ和σ的技能在实际生活中有广泛应用:
The skill of finding unknown parameters μ and σ has wide applications in real life:
-
质量控制 / Quality Control: 根据产品合格率确定生产标准
Determining production standards based on product qualification rates -
医学研究 / Medical Research: 根据疾病分布确定正常值范围
Determining normal value ranges based on disease distribution -
教育评估 / Educational Assessment: 根据考试成绩分布确定评分标准
Determining grading standards based on exam score distribution -
金融风险管理 / Financial Risk Management: 根据历史数据确定风险参数
Determining risk parameters based on historical data