练习题1:基本梯度函数绘制
为以下各图绘制对应的梯度函数图像,标出与x轴相交或相切的点,并给出渐近线方程。
图a) 和 图b)
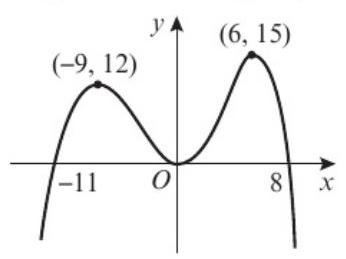
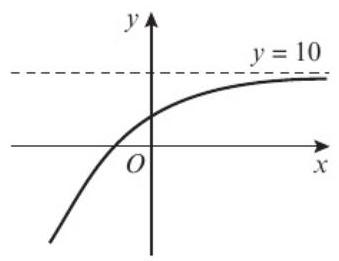
你的答案
1. 识别原函数的极值点和拐点;2. 分析各区间的斜率符号;3. 找出渐近线的位置;4. 按照特征对应关系绘制。
练习题2:复杂函数梯度函数绘制
为以下各图绘制对应的梯度函数图像,标出与x轴相交或相切的点,并给出渐近线方程。
图c) 和 图d)
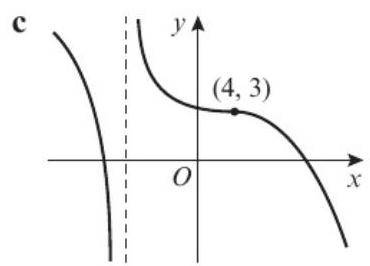
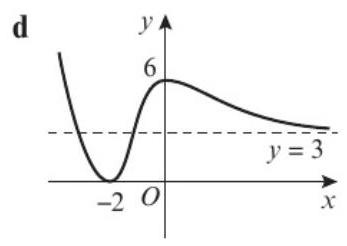
你的答案
1. 注意识别垂直渐近线和水平渐近线;2. 分析拐点和极值点的位置;3. 确定各区间的增减性;4. 综合所有特征绘制。
练习题3:特殊函数分析
为以下各图绘制对应的梯度函数图像,标出与x轴相交或相切的点,并给出渐近线方程。
图e) 和 图f)
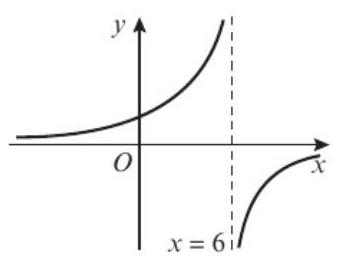
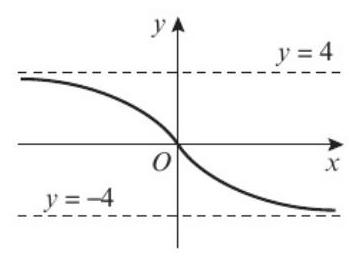
你的答案
1. 特别注意渐近线的位置和类型;2. 分析函数在不同区间的行为;3. 找出所有关键特征点;4. 按照对应关系绘制。
问题P2:多项式函数分析
题目描述:函数 \( f(x) = (x + 1)(x - 4)^2 \)
a) 绘制函数 \( y = f(x) \) 的图像。
b) 在单独的坐标轴上绘制梯度函数 \( y = f'(x) \) 的图像。
c) 证明 \( f'(x) = (x - 4)(3x - 2) \)。
d) 用导数确定梯度函数与坐标轴相交的确切坐标。
你的答案
a) 这是一个三次函数,在x=-1和x=4处有零点,x=4是重零点;b) 先求导数,然后分析特征;c) 展开原函数后求导,或用乘积法则;d) 令f'(x)=0求驻点,令f'(x)=0和f''(x)=0求拐点。