7.3 绘制梯度函数
你可以通过给定函数的特征来绘制其对应的梯度函数。下表展示了函数 \( y = f(x) \) 的图像特征与梯度函数 \( y = f'(x) \) 的图像特征之间的对应关系。
特征对应表
| \( y = f(x) \) 的特征 | \( y = f'(x) \) 的特征 |
| 极大值或极小值点 | 与x轴相交 |
| 拐点 | 与x轴相切 |
| 正斜率 | 在x轴上方 |
| 负斜率 | 在x轴下方 |
| 垂直渐近线 | 垂直渐近线 |
| 水平渐近线 | 以x轴为水平渐近线 |
注意
忽略函数与x轴的交点。这些点不会告诉你在梯度函数图像的特征方面有任何信息。
Example 5
由梯度函数图像反推原函数特征
题目(与图像一致):下图给出了梯度函数 \(y=f'(x)\) 的图像。图像与 x 轴相交于 \(x=-1\)、\(x=1\),且在 \(x<-1\) 和 \(x>1\) 时位于 x 轴上方,在 \(-1
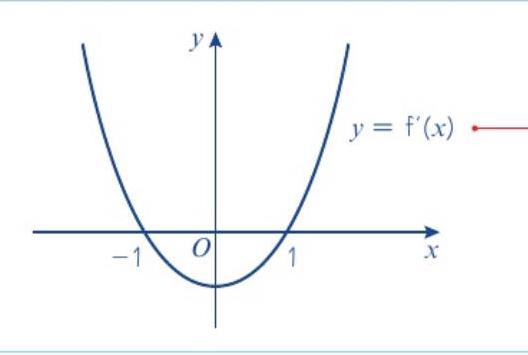
Example 6
含渐近线情形:由 \(f(x)\) 推 \(f'(x)\)
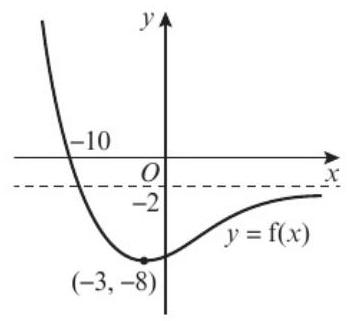
题目:下图显示了函数 \( y = f(x) \) 的图像。该曲线有水平渐近线 \( y = -2 \),在点 (-3, -8) 处有拐点,在点 (-10, 0) 处与 x 轴相交。
- a) 在单独坐标系中绘制梯度函数 \(y=f'(x)\) 的图像,并标出与 x 轴交点/相切点。
- b) 写出 \(y=f'(x)\) 的渐近线方程(提示:水平渐近线应为 \(y=0\))。
- c) 指出 \(x=-3\) 处为何为相切点,并据此讨论 \(f(x)\) 在该点的性质(拐点)。

方法要点与检查
要点
1) 先分析原函数的特征;2) 忽略与x轴交点;3) 确定极值点对应相交,拐点对应相切;4) 渐近线传递;5) 根据斜率符号确定位置。