Exercise 8D - 曲线与直线间面积
1. 基础曲线与水平线
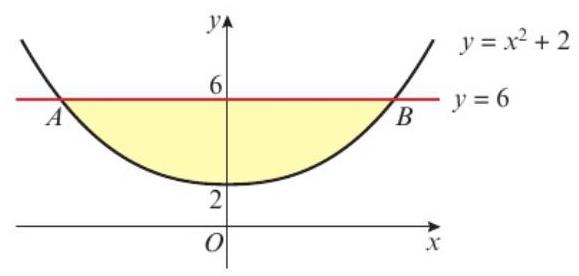
The diagram shows part of the curve with equation \(y = x^2 + 2\) and the line with equation \(y = 6\).
The line cuts the curve at the points A and B.
a) Find the coordinates of the points A and B.
b) Find the area of the finite region bounded by line AB and the curve.
a) A(-2, 6), B(2, 6)
b) Area = 16 - \(\frac{32}{3}\) = \(\frac{16}{3}\)