Exercise 8E - 两条曲线间面积
1. 基础两条曲线间面积
Find, using calculus, the finite area bounded by the curve \(y = 2x^2 - 8x - 10\), the curve \(y = \frac{x^2}{2} - 2x - 1\) and the lines \(x = 1\) and \(x = 3\).
Area = \(\int_1^3 (2x^2 - 8x - 10) - (\frac{x^2}{2} - 2x - 1) dx\)
= \(\int_1^3 (\frac{3x^2}{2} - 6x - 9) dx\)
= \(\left[\frac{x^3}{2} - 3x^2 - 9x\right]_1^3\)
= \(\frac{27}{2} - 27 - 27 - (\frac{1}{2} - 3 - 9)\)
= \(-\frac{27}{2} - (-\frac{11}{2}) = -8\)
注意:面积为8(取绝对值)
2. 两条抛物线间面积
The curve C with equation \(y = x^2\) and the curve S with equation \(y = 2x^2 - 25\) intersect at two points.
Using algebraic integration calculate the finite region enclosed by C and S.
交点:\(x^2 = 2x^2 - 25\)
\(x^2 = 25\)
\(x = \pm 5\)
Area = \(\int_{-5}^5 (2x^2 - 25) - x^2 dx\)
= \(\int_{-5}^5 (x^2 - 25) dx\)
= \(\left[\frac{x^3}{3} - 25x\right]_{-5}^5\)
= \(\frac{125}{3} - 125 - (-\frac{125}{3} + 125)\)
= \(-\frac{250}{3}\)
注意:面积为\(\frac{250}{3}\)(取绝对值)
3. 复杂曲线间面积
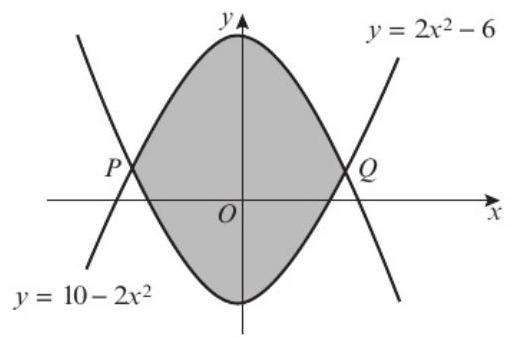
The curves with equations \(y = 2x^2 - 6\) and \(y = 10 - 2x^2\) intersect at points P and Q as shown in the diagram.
Use calculus to calculate the area of the finite region enclosed by these curves.
交点:\(2x^2 - 6 = 10 - 2x^2\)
\(4x^2 = 16\)
\(x = \pm 2\)
Area = \(\int_{-2}^2 (10 - 2x^2) - (2x^2 - 6) dx\)
= \(\int_{-2}^2 (16 - 4x^2) dx\)
= \(\left[16x - \frac{4x^3}{3}\right]_{-2}^2\)
= \(32 - \frac{32}{3} - (-32 + \frac{32}{3})\)
= \(\frac{128}{3}\)
4. 三次函数与二次函数
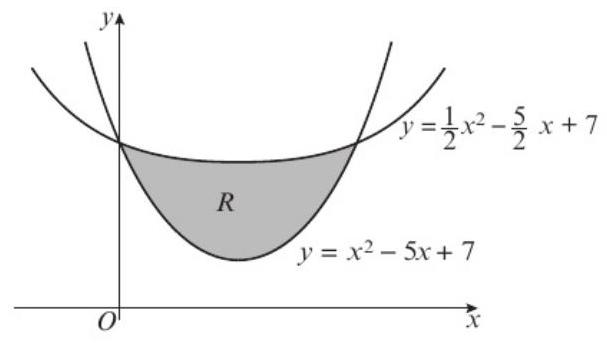
The diagram above shows part of the curves \(y = x^3 + x^2\) and \(y = 2x^2 + 2x\).
Use calculus to calculate the area of the finite region enclosed.
交点:\(x^3 + x^2 = 2x^2 + 2x\)
\(x^3 - x^2 - 2x = 0\)
\(x(x^2 - x - 2) = 0\)
\(x = 0\) 或 \(x = 2\) 或 \(x = -1\)
Area = \(\int_{-1}^0 (x^3 + x^2) - (2x^2 + 2x) dx + \int_0^2 (2x^2 + 2x) - (x^3 + x^2) dx\)
= \(\int_{-1}^0 (x^3 - x^2 - 2x) dx + \int_0^2 (-x^3 + x^2 + 2x) dx\)
= \(\left[\frac{x^4}{4} - \frac{x^3}{3} - x^2\right]_{-1}^0 + \left[-\frac{x^4}{4} + \frac{x^3}{3} + x^2\right]_0^2\)
= \(\frac{7}{12} + \frac{8}{3} = \frac{13}{4}\)
5. 两条二次函数
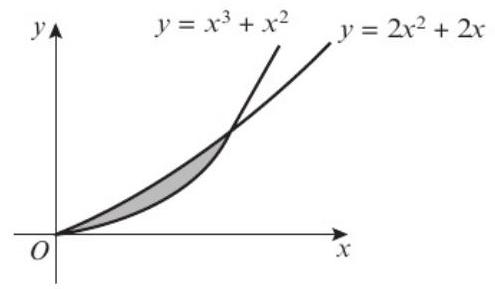
The curve with equation \(y = x^2 - 5x + 7\) cuts the curve with equation \(y = \frac{1}{2}x^2 - \frac{5}{2}x + 7\).
The shaded region R is bounded by the curves as shown.
Find the exact area of R.
交点:\(x^2 - 5x + 7 = \frac{1}{2}x^2 - \frac{5}{2}x + 7\)
\(\frac{1}{2}x^2 - \frac{5}{2}x = 0\)
\(x(\frac{1}{2}x - \frac{5}{2}) = 0\)
\(x = 0\) 或 \(x = 5\)
Area = \(\int_0^5 (x^2 - 5x + 7) - (\frac{1}{2}x^2 - \frac{5}{2}x + 7) dx\)
= \(\int_0^5 (\frac{1}{2}x^2 - \frac{5}{2}x) dx\)
= \(\left[\frac{x^3}{6} - \frac{5x^2}{4}\right]_0^5\)
= \(\frac{125}{6} - \frac{125}{4} = -\frac{125}{12}\)
注意:面积为\(\frac{125}{12}\)(取绝对值)