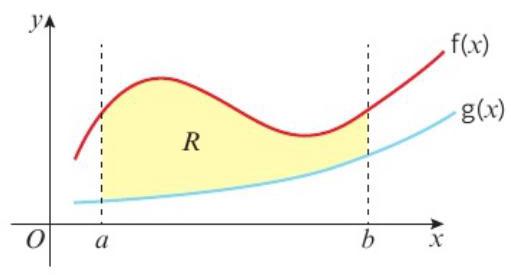
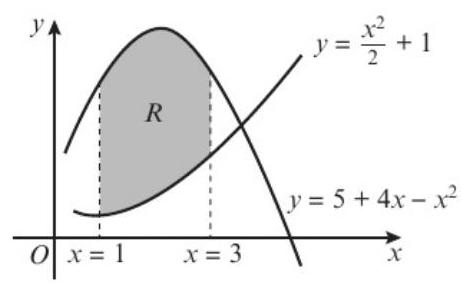
题目:
The diagram below shows a sketch of part of the curve S with equation \(y = 8 - 2x - x^2\)
The curve T with equation \(y = x^2 + x + 6\) intersects S at two points.
a) Find the x-coordinates of the points of intersection of S and T.
b) Use calculus to find the area of the finite region bounded by S and T.
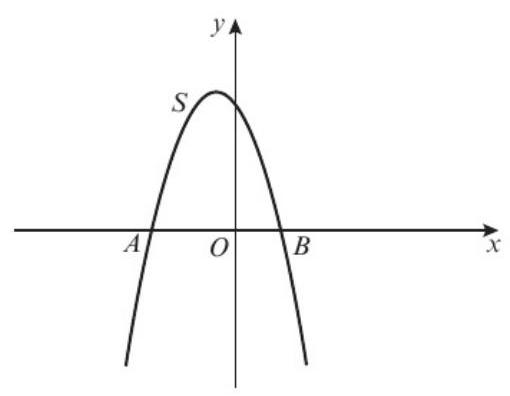
图3:Example 2 - 曲线S和T的交点示意图
解:
- 求交点:\(8 - 2x - x^2 = x^2 + x + 6\)
- \(2x^2 + 3x - 2 = 0\)
- \((2x - 1)(x + 2) = 0\)
- \(x = -2\) 或 \(x = \frac{1}{2}\)
b) Area = \(\int_{-2}^{0.5} (8 - 2x - x^2) - (x^2 + x + 6) dx\)
Area = \(\int_{-2}^{0.5} (2 - 3x - 2x^2) dx\)
Area = \(\left[2x - \frac{3x^2}{2} - \frac{2x^3}{3}\right]_{-2}^{0.5}\)
Area = \(\frac{125}{24}\)