精选复习题目
1. 基础定积分计算
a) Find \(\int (x^{\frac{1}{2}} - 4)(x^{-\frac{1}{2}} - 1) dx\).
b) Use your answer to part a to evaluate \(\int_1^4 (x^{\frac{1}{2}} - 4)(x^{-\frac{1}{2}} - 1) dx\) giving your answer as an exact fraction.
a) \((x^{\frac{1}{2}} - 4)(x^{-\frac{1}{2}} - 1) = 1 - x^{\frac{1}{2}} - 4x^{-\frac{1}{2}} + 4\)
= \(5 - x^{\frac{1}{2}} - 4x^{-\frac{1}{2}}\)
\(\int (5 - x^{\frac{1}{2}} - 4x^{-\frac{1}{2}}) dx = 5x - \frac{2}{3}x^{\frac{3}{2}} - 8x^{\frac{1}{2}} + C\)
b) \(\int_1^4 (5 - x^{\frac{1}{2}} - 4x^{-\frac{1}{2}}) dx\)
= \(\left[5x - \frac{2}{3}x^{\frac{3}{2}} - 8x^{\frac{1}{2}}\right]_1^4\)
= \(20 - \frac{16}{3} - 16 - (5 - \frac{2}{3} - 8)\)
= \(-\frac{16}{3} + \frac{2}{3} = -\frac{14}{3}\)
2. 分数幂函数积分
Consider the function \(y = 3x^{\frac{1}{2}} - 4x^{-\frac{1}{2}}, x > 0\).
a) Find \(\frac{dy}{dx}\).
b) Find \(\int y dx\).
c) Hence show that \(\int_1^3 y dx = A + B\sqrt{3}\), where A and B are integers to be found.
a) \(\frac{dy}{dx} = 3 \times \frac{1}{2}x^{-\frac{1}{2}} - 4 \times (-\frac{1}{2})x^{-\frac{3}{2}}\)
= \(\frac{3}{2}x^{-\frac{1}{2}} + 2x^{-\frac{3}{2}}\)
b) \(\int y dx = \int (3x^{\frac{1}{2}} - 4x^{-\frac{1}{2}}) dx\)
= \(3 \times \frac{2}{3}x^{\frac{3}{2}} - 4 \times 2x^{\frac{1}{2}} + C\)
= \(2x^{\frac{3}{2}} - 8x^{\frac{1}{2}} + C\)
c) \(\int_1^3 y dx = \left[2x^{\frac{3}{2}} - 8x^{\frac{1}{2}}\right]_1^3\)
= \(2 \times 3\sqrt{3} - 8\sqrt{3} - (2 - 8)\)
= \(6\sqrt{3} - 8\sqrt{3} + 6 = -2\sqrt{3} + 6\)
所以 A = 6,B = -2
3. 复合函数面积计算
The diagram shows part of the curve with equation \(y = p + 10x - x^2\), where p is a constant, and part of the line l with equation \(y = qx + 25\), where q is a constant. The line l cuts the curve at the points A and B. The x-coordinates of A and B are 4 and 8 respectively.
a) Show that p = -7 and calculate the value of q.
b) Calculate the coordinates of C.
c) The shaded region in the diagram is bounded by the curve and the line segment AC. Using integration and showing all your working, calculate the area of the shaded region.
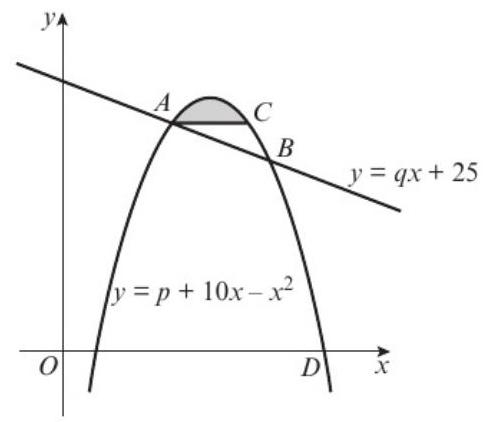
a) 在x = 4处:\(p + 40 - 16 = 4q + 25\),即 \(p + 24 = 4q + 25\)
在x = 8处:\(p + 80 - 64 = 8q + 25\),即 \(p + 16 = 8q + 25\)
解得:p = -7,q = -2
b) C的坐标:(8, 9)
c) Area = \(\int_4^8 (-7 + 10x - x^2) - (-2x + 25) dx\)
= \(\int_4^8 (-32 + 12x - x^2) dx\)
= \(\left[-32x + 6x^2 - \frac{x^3}{3}\right]_4^8\)
= \(-256 + 384 - \frac{512}{3} - (-128 + 96 - \frac{64}{3})\)
= \(\frac{64}{3}\)
4. 梯形法则应用
a) Complete the table below, giving the values of y to 3 decimal places.
\(y = \sqrt{3^x + x}\)
b) Use the trapezium rule with all of the values of y from your table to find an approximation for the value of \(\int_0^1 \sqrt{3^x + x} dx\).
a) 完成表格:
x = 0.5时,y = √(1.732 + 0.5) = √2.232 ≈ 1.494
x = 0.75时,y = √(2.280 + 0.75) = √3.030 ≈ 1.741
b) h = 0.25
Area ≈ ½ × 0.25 × (1 + 2(1.251 + 1.494 + 1.741) + 2)
≈ 0.125 × (1 + 8.972 + 2) = 1.496
5. 两条曲线间面积
The curve A with equation \(y = 8 + 4x - x^2\) and the curve B with equation \(y = x^2 - 4x + 8\) intersect at two points M and N.
a) Find the coordinates of M and the coordinates of N.
b) Use calculus to find the area of the finite region enclosed by A and B.
a) \(8 + 4x - x^2 = x^2 - 4x + 8\)
\(4x - x^2 = x^2 - 4x\)
\(8x - 2x^2 = 0\)
\(2x(4 - x) = 0\)
\(x = 0\) 或 \(x = 4\)
M(0, 8),N(4, 8)
b) Area = \(\int_0^4 (8 + 4x - x^2) - (x^2 - 4x + 8) dx\)
= \(\int_0^4 (8x - 2x^2) dx\)
= \(\left[4x^2 - \frac{2x^3}{3}\right]_0^4\)
= 64 - \(\frac{128}{3} = \frac{64}{3}\)