Question 1 - 曲线与直线间面积
题目:
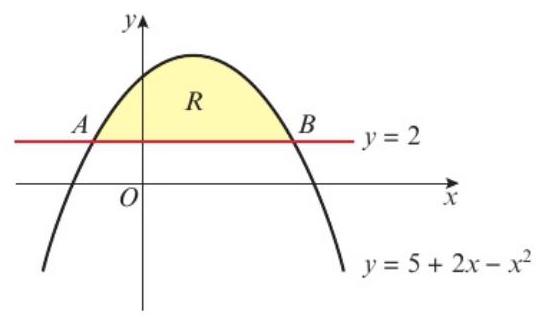
The diagram shows the curve with equation \(y = 5 + 2x - x^2\) and the line with equation \(y = 2\). The curve and the line intersect at the points A and B.
a) Find the x-coordinates of A and B.
b) The shaded region R is bounded by the curve and the line. Find the area of R.
解:
- a) 求交点:\(5 + 2x - x^2 = 2\)
- \(3 + 2x - x^2 = 0\)
- \(x^2 - 2x - 3 = 0\)
- \((x - 3)(x + 1) = 0\)
- \(x = -1\) 或 \(x = 3\)
b) Area = \(\int_{-1}^3 (5 + 2x - x^2) dx - \int_{-1}^3 2 dx\)
= \(\int_{-1}^3 (3 + 2x - x^2) dx\)
= \(\left[3x + x^2 - \frac{x^3}{3}\right]_{-1}^3\)
= \(9 + 9 - 9 - (-3 + 1 + \frac{1}{3}) = \frac{32}{3}\)